初探机器学习-梯度下降法求解最优值

什么是模型

只要是从事IT行业想必都对机器学习有所耳闻。关于机器学习我们平常听到最多的名词可能就是算法模型。那么算法模型究竟是什么东西呢

在回答这个问题之前我们先来看一个简单的例子

现在有一份这样的数据只有两个字段

size,price
1,2
2,4
3,6
4,8
5,10
6,12

这个数据只有两个字段一个是物品的大小一个是物品的价格。现在老板给了一个需求希望你可以开发出一个功能给定一个物品的大小就能得到这个物品的价格。

你瞄了一眼这份数据心想这不太简单了然后开始敲代码

public int getPrice(int size) {
    return size * 2;
}

到这里你其实已经得到了一个很简单的算法模型price = size * 2。和平常机器学习不同的是这份数据太简单了简单到你瞄一眼就可以从数据中得出这个算法模型。你在脑子里完成了这个训练的过程。

现在我们来回答下什么是机器学习的模型

在大部分机器学习的场景下算法模型其实可以理解为一个函数比如y=2x。当然各种算法模型对应的函数远比上面介绍的price=size*2要来的复杂。很多机器学习算法的目的就是通过训练已有的数据找出最符合数据规律的那个函数。

如何训练模型

上面我们已经了解到模型就是一个可以完成特定功能的函数。那么我们如何得到这个函数呢

我们还是通过一个例子来了解一下这个过程。现在老板又搞来一份数据让你通过这份数据找出size和price的映射关系。

size,price
7,46
9,39
8,38
10,49
17,84
16,80
11,45
5,37
2,13
1,16

这时你可能会有点懵这数据好像一时半会也看不出什么规律更别提找什么映射关系了。这时要靠我们自己已经很难出这份数据中训练出那个模型了。因此这时候就需要引入机器学习的相关知识。下面我们来看一下针对这种线性回归的预测问题最简单的模型训练方法是怎么进行的。

1、拟定假设函数

首先我们的目标是找出可以很好拟合这份数据的函数函数长什么样一开始我们是完全不知道的。因此一开始需要先定义一个假设函数。这个假设函数需要根据数据的分布情况去定义。我们可以简单绘制下上面这份数据的分布情况

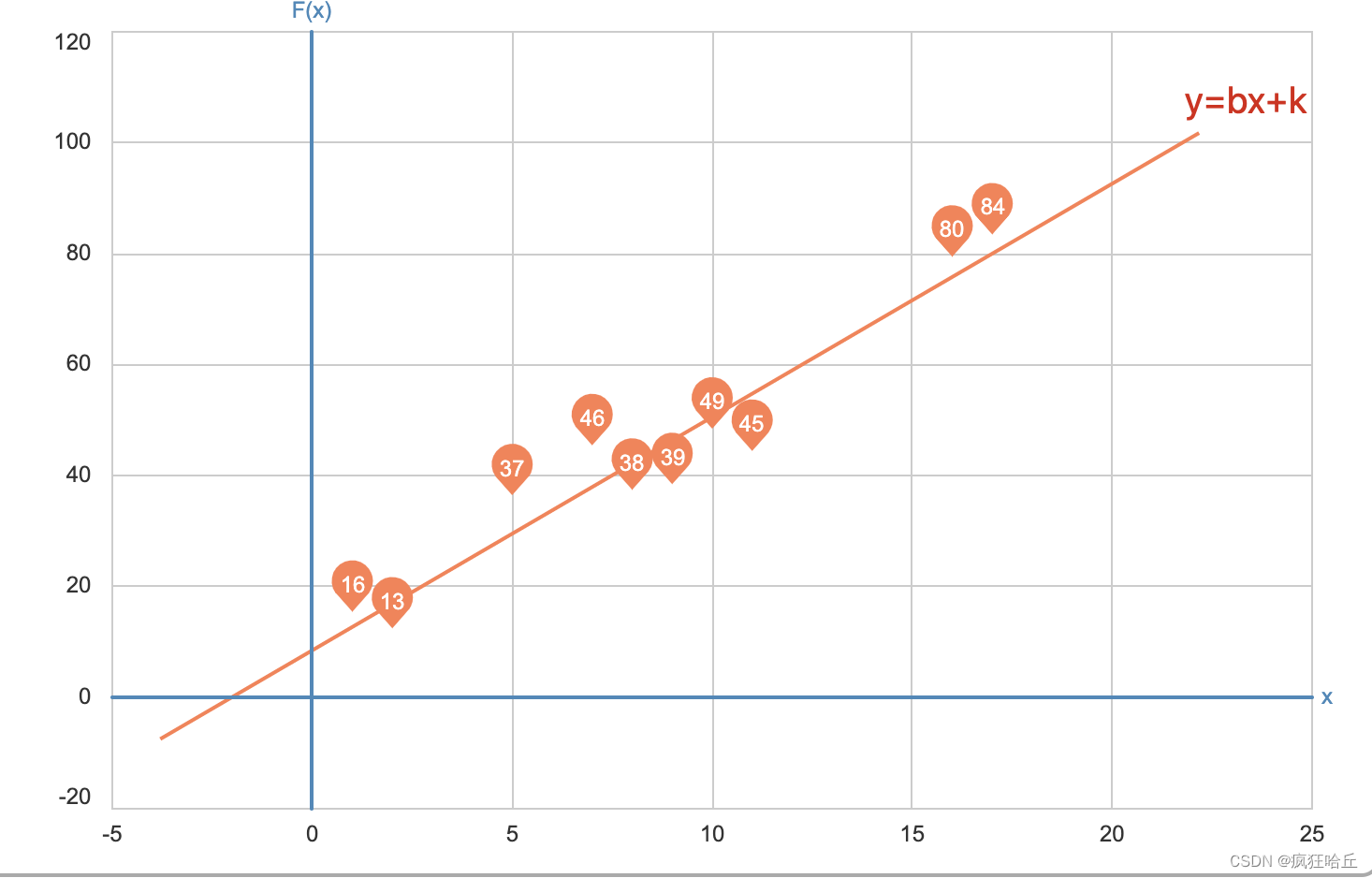
通过绘制数据点的分布情况我们发现这个数据可以用一个函数 y = wx + b 来表示。其中x表示数据的sizey表示数据的price。w和b目前都是未知的随着w和b的变动这条线的斜率也会发生变动。

现在确定下来假设函数为 y = wx + b 我们下一步要做的就是在所有w和b的取值中找出最能拟合这份数据的值。

2、损失函数和代价函数

确定了假设函数后下一步要做的事情就是找出w和b的最优解。那么如何定义怎么样才算最优解呢

这里需要引入两个概念损失函数和代价函数。

首先是损失函数
$$Loss(w,b)=|y_i-(w{x}_i+b)|$$
这个函数是一个二元一次方程式xi和yi表示具体的数据它的含义是指数据中某个点到这条直线的垂直距离比如对于(746)这个点来说它的损失值(误差值)可以这么理解

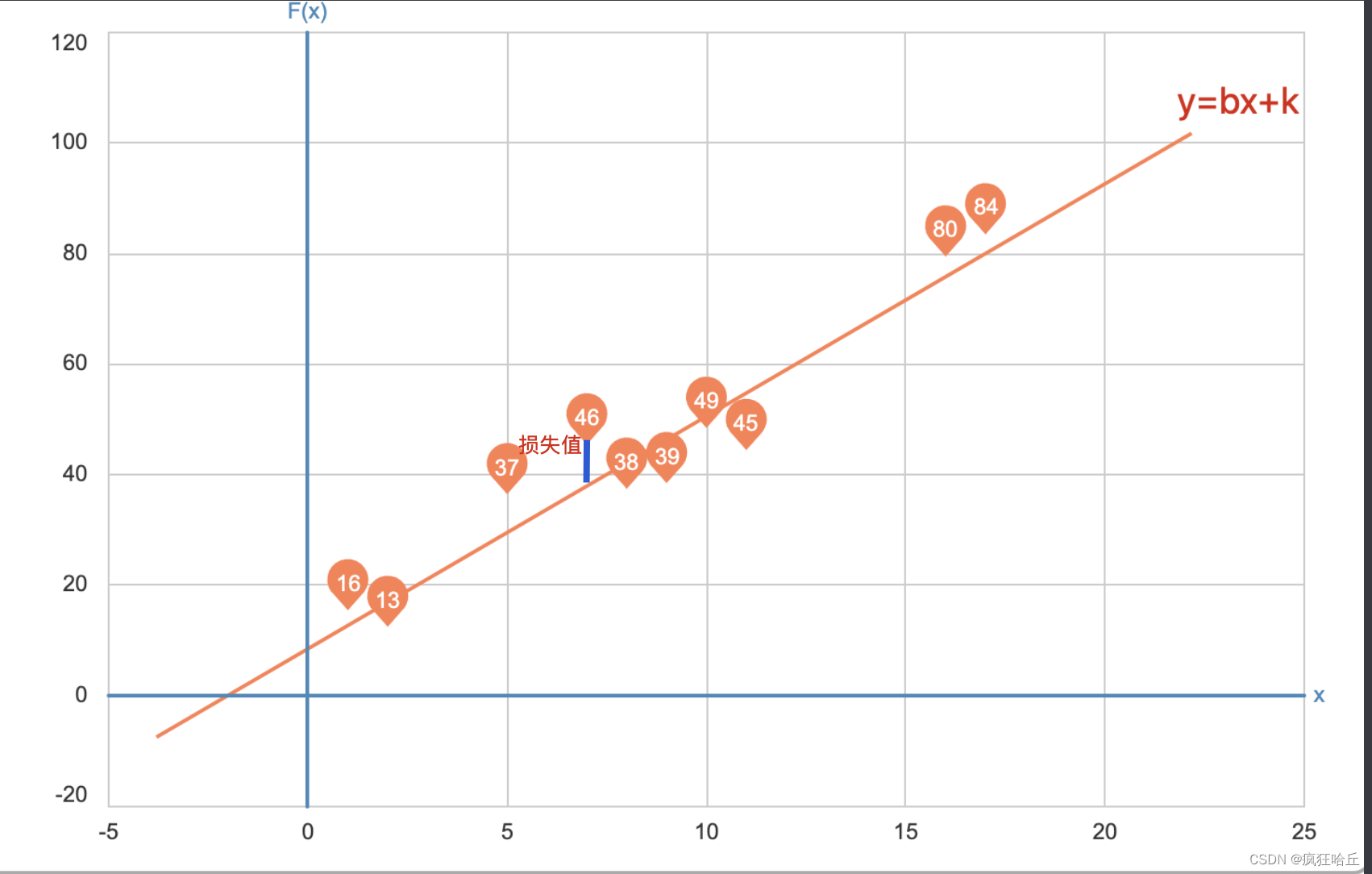
为了更方便理解我们可以假设b=2k=2那么这时候我们的假设函数为y=2x+2此时(7,46)这个点的损失值为 46 -2 *7 + 2= 34。

现在我们知道了损失函数代表某个点的偏差值那么代价函数其实就是将所有点的偏差值都累加起来然后求平均。
$$Cost(w,b)=\frac{1}{2m}\sum _{i=0}^m(y_i-(w{x}_i+b){)}^2$$

上面的代价函数还是一个二元一次方程式。其中对 yi- (wxi +b)求平方是为了保证偏差结果为正。左边总偏差除以m是为了求平均又多除了一个2是为了后面方便求导数。因为我们最终需要通过求导的方式来获得最优解。

到这里为止我们得到了一个二元一次的代价函数Cost(w,b)这里w和b可以为任意值我们需要知道当w和b的值分别为多少时可以使这个函数达到最小值。因此问题就变成了数学中的求极值问题。对于如何求解一个函数的最大值或最小值最常用的一个方法是对函数求导。

3、关于导数和偏导数

下面我们先来复习下关于导数的意义

导数是当函数y=fx的自变量x在一点x0上产生一个增量Δx时函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在a即为在x0处的导数记作f’x0或dfx0/dx。

一时看不懂也没关系我们只要记住一句话导数的几何意义是该函数曲线在这一点上的切线斜率

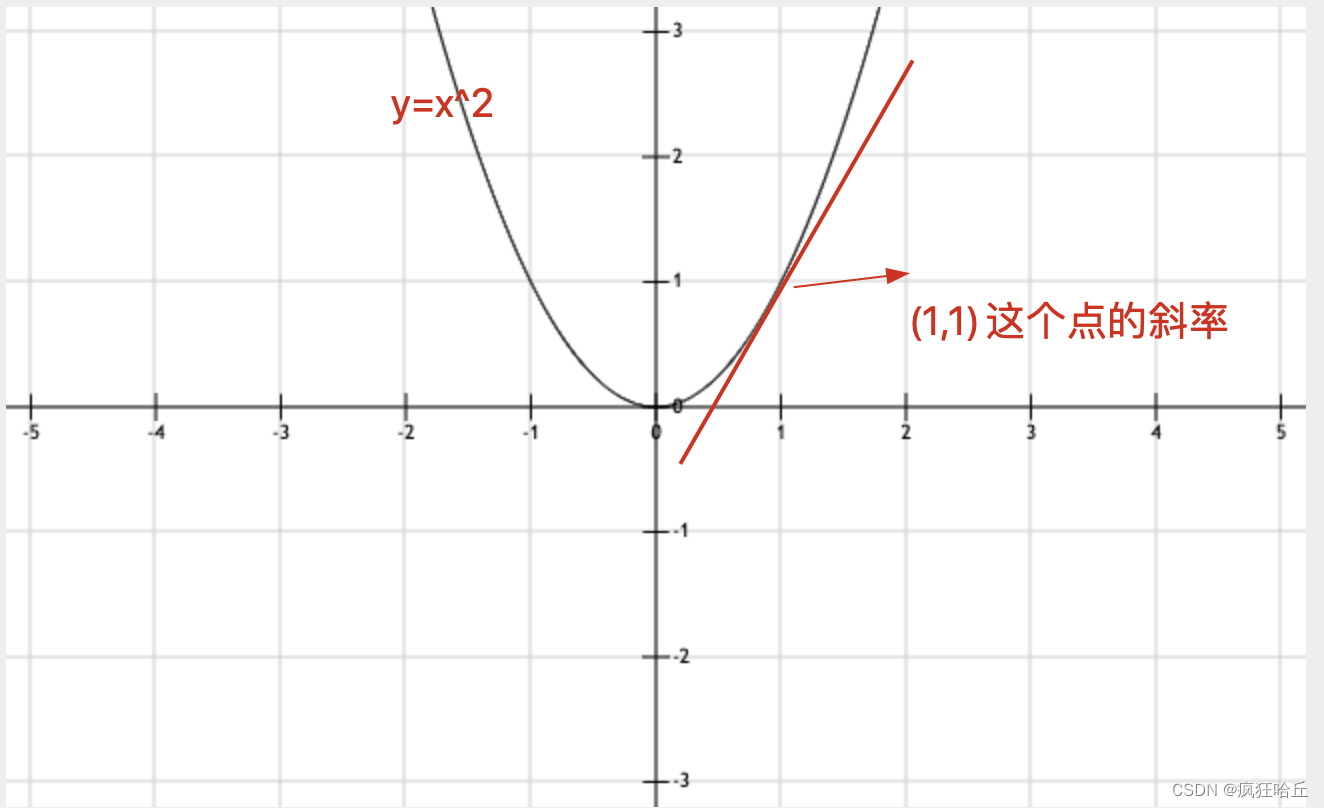
上面这张图是y=x^2这条曲线它的导函数为 y' = 2x 。那么它在(1,1) 这个点的求导值就是2也就是这个点切线的斜率。

常见的求导公式

到这里可能大家就会问知道一个点的斜率有什么用呢答案是可以用来求最优解当斜率为0时我们可以认为达到了某段曲线的最大值或者最小值。

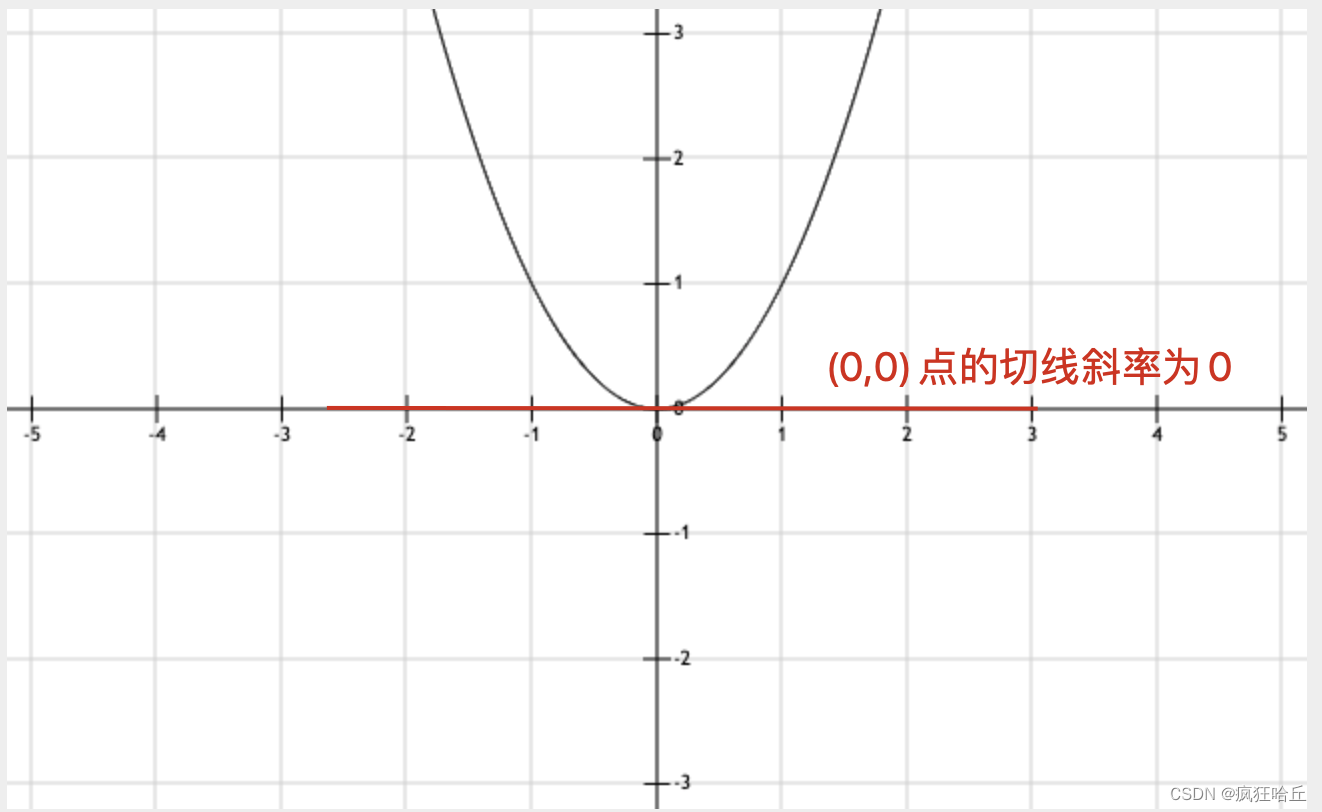
还是上面那幅图我们发现(0,0)的切线斜率为0而该点也是整个曲线的最小值。

需要注意的是切线斜率为0只能说明是局部最优解并不意味着是全局最优解。因为有些函数的曲线可能非常复杂有多个坡的坡顶斜率都刚好为0可以想象一下山峰。

理解了导数之后我们再来看偏导数。导数是对单个变量进行求导而如果函数中有多个变量则需要用上偏导数。偏导数其实将其他的变量当成常数然后对某个变量求导。

比如偏导数 f’x(x0,y0) 表示固定面上一点对 x 轴的切线斜率。偏导数 f’y(x0,y0) 表示固定面上一点对 y 轴的切线斜率。

上面的代价函数Cost(w,b)是一个二元一次方程因此我们需要利用偏导数来求解最优值。

4、使用梯度下降法求解最优值

梯度下降法是用来求解函数最小值的。

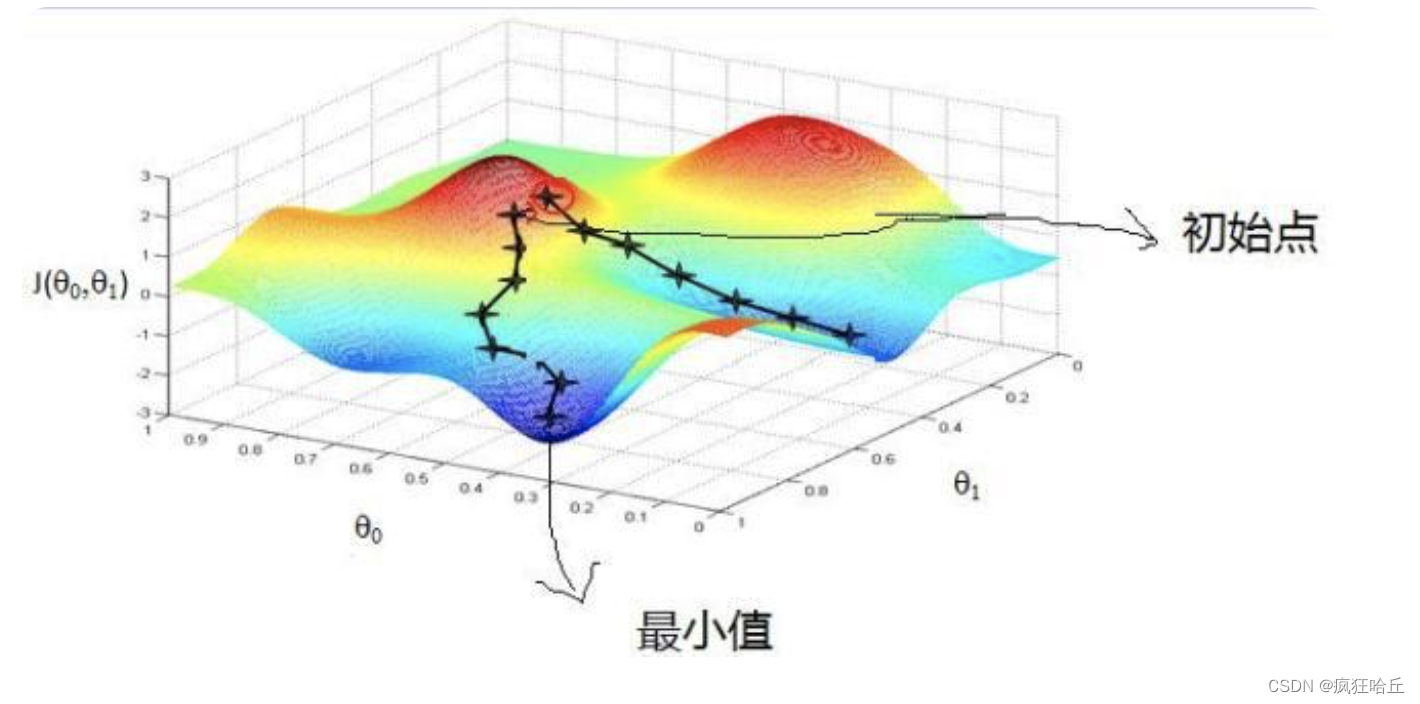
我们以上面的图为例假设一个人处于红色位置的山顶那么该如何到达蓝色区域的山底呢。按照梯度下降法的思想它大概会这么操作

1、找到当前位置下降最快的方向

2、往下降最快的方向走一小步到达新的位置

之后不断重复上面两个步骤直到到达山坡最低点为止。

到这里你可能会发现站到不同的初始位置通过梯度下降法最终走到的最低点是不一样的。是的因为上图不是标准的凸函数所以往往不能找到全局的最小值只能找到局部的最小值。所以我们可以使用不同的初始位置来寻找更小的级小值点。

回到梯度下降算法上来我们知道了算法的大致思路是往下降最快的方向走。那哪个方向才是下降最快的方向呢这就需要结合导数的知识了。为了更方便理解我们还是以二维坐标轴的方式展开。我们之前说了导数的几何意义是该函数曲线在这一点上的切线斜率。下面我们来观察下(-1,1) 和 (1,1) 这两个点的导数

对于y=x^2这个曲线

(-1,1)这个点的斜率为-2此时下降最快的方向是右也就是通过增加x的值可以达到最低点

(1,1)这个点的斜率为2此时下降最快的方向是左也就是通过减少x的值可以达到最低点

这里我们就可以得到一个结论假设 f’(x0) 为某个点在曲线上的导数那么 -f’(x0) 就是下降最快的方向。带着这个结论我们来模拟下梯度下降法寻找最小值的过程

设定初始值为x=2。函数为y=x^2导函数为y=2x。为了让每一步试探的步伐不会太大这里还需要引入一个步频有些地方也叫学习率、或者叫步长这里暂定步频为0.25

1、对x=2求导得到导数值为4。也就是我们需要向左走 4 * 0.25 = 1 (步长 = 导数的负数 * 步频)。也就是 x=2-1此时来到点 (1,1) 的位置

2、此时x=1对其求导得到导数值为2。此时需要向左走 2 * 0.25 = 0.5。也就是x=1-0.5此时来到点(0.5,0.25)处

3、此时x=0.5对其求导得到导数值为1此时需要向左走 1 * 0.25 = 0.25。也就是x = 0.5 - 0.25此时来到点(0.25,0.0625)处

4、继续迭代…

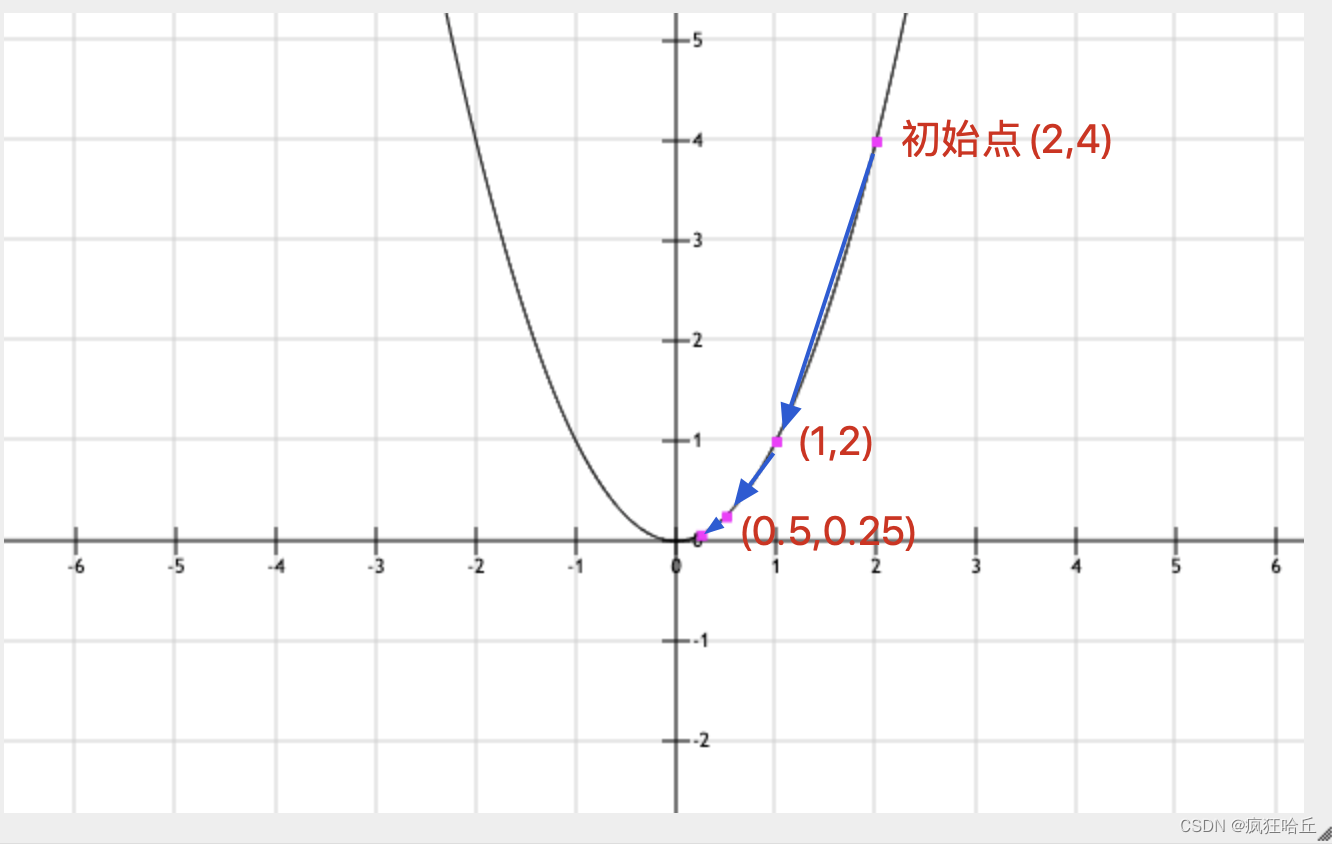
这样不断迭代下去我们会发现这样只能不断的逼近最低点事实也是如此通过梯度下降法我们只能获取一个无限接近最优解的值而无法到达因此我们需要给整个迭代设置一个终止条件。通过上面几步迭代我们可以看出随着离最低点越来越近每一步可以移动的距离会越来越小。因此我们可以设置是个阈值比如当移动的步长小于某个值时终止迭代。假设这个阈值为0.26那么在我们的模拟迭代中完成第三次之后迭代就结束了第三次的步长为 0.25刚好小于0.26。不难想象设置越低的阈值可以得到更接近最优解的值。

关于步频

上面我们有引入一个步频的概念。那么引入这个概念的目的是什么呢。主要是为了防止每次移动的步长过大或者过小。

可以看到步频如果过小会导致迭代了很多次都离最低点很远。而步频较大或者过大会导致迭代时反复在最低点的两边反复横条永远无法到达最低点。甚至可能离最低点越来越远。因此步频的选择是一个技术活需要根据经验和实际场景来调整。

接下来让我们将梯度下降法从二维平面扩展到三维图形上来就可以用来求解我们前面提到的代价函数的最小值了。为了方便表达我们将Cost(w,b) 的结果定义为z。
$$z=\frac{1}{2m}\sum _{i=0}^m(y_i-(w{x}_i+b){)}^2$$

这样这个代价函数就是由w、b、z三个维度组成的三维空间了。它在三维空间生成的平台可能长这样

现在我们要求z的最小值这时候我们使用梯度下降法寻找下降最快的方向时就需要由w和b共同决定比如对于w而言需要确定是增加w的值还是减少w的值。因此需要分别对w和b求他们的偏导函数

首先w的偏导函数为
$$\frac{\delta (z)}{\delta (w)}=\frac{1}{2m}\sum _{i=0}^{m}2\ast (y_i-(w{x}_i+b))\ast x_i$$
b的偏导函数为
$$\frac{\delta (z)}{\delta (b)}=\frac{1}{2m}\sum _{i=0}^{m}2\ast (y_i-(w{x}_i+b))$$

想了解这两个偏导函数具体是如何推导出来的可以看这篇https://zhuanlan.zhihu.com/p/36783863

知道这两个偏导函数之后我们就可以开始使用梯度下降法寻找z的最小值了

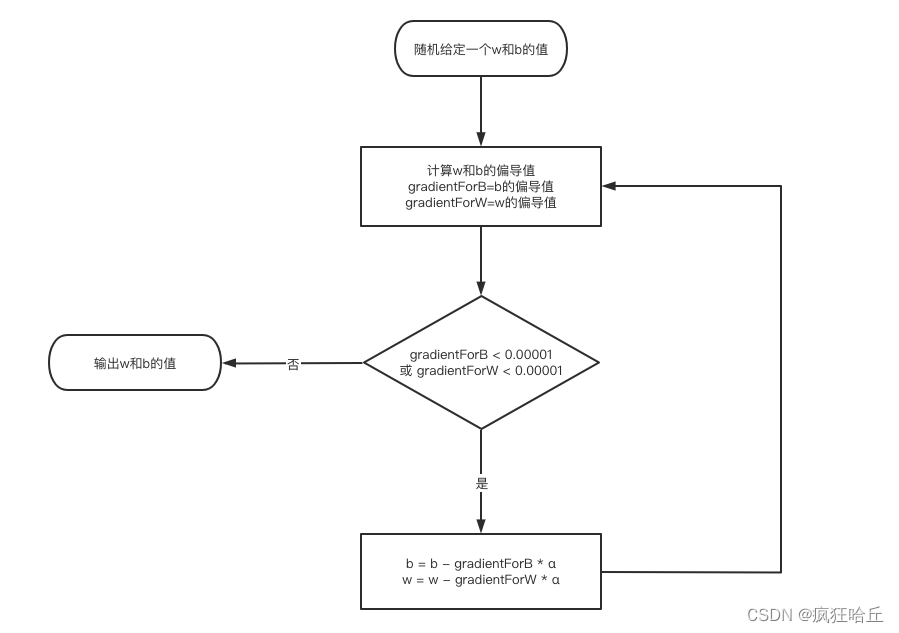
用代码实现也很简单

    public static void main(String[] args) throws IOException {
        //从数据文件读取数据
        //数据格式为(x和y用逗号隔开)
        //1,2
        //2,4
        //3,6
        final List<String> lines = FileUtils.readLines(new File("/tmp/test.data"));
        int[] x = new int[lines.size()];
        int[] y = new int[lines.size()];
        for (int i = 0; i < lines.size(); i++) {
            final String[] array = lines.get(i).split(",");
            x[i] = Integer.parseInt(array[0]);
            y[i] = Integer.parseInt(array[1]);
        }

        //给定一个最大的迭代次数避免无限迭代下去
        int tryTimes = 0;
        //给定一个w和b的初始值
        double b = 10000;
        double w = 10000;
        //通过偏导函数求得下降的方向和距离
        double gradientForB = partialFunctionForB(x, y, b, w);
        double gradientForW = partialFunctionForW(x, y, b, w);
        //步频(学习率)
        double alpha = 0.01;
        while ((Math.abs(gradientForB) >= 0.000001 || Math.abs(gradientForW) >= 0.000001) && tryTimes < 1000000) {
            b = b - alpha * gradientForB;
            w = w - alpha * gradientForW;
            gradientForB = partialFunctionForB(x, y, b, w);
            gradientForW = partialFunctionForW(x, y, b, w);
            tryTimes++;
        }
        System.out.printf("function is : y = %.5f * x + %.5f\n", w, b);
        System.out.printf("iteration count:%d", tryTimes);
    }

    //假设函数
    public static double hypothesisFunction(int x, double b, double w) {
        return w * x + b;
    }

    //对b的偏导函数
    public static double partialFunctionForB(int[] x, int[] y, double b, double w) {
        double sum = 0;
        for (int i = 0; i < x.length; i++) {
            //求偏导函数
            sum += 2 * (hypothesisFunction(x[i], b, w) - y[i]);
        }
        return sum / 2 / x.length;
    }

    //对w的偏导函数
    public static double partialFunctionForW(int[] x, int[] y, double b, double w) {
        double sum = 0;
        for (int i = 0; i < x.length; i++) {
            sum += 2 * (hypothesisFunction(x[i], b, w) - y[i]) * x[i];
        }
        return sum / 2 / x.length;
    }

最后我们就得到了w和b的值代入假设函数 y = wx + b 就可以得到我们训练出的模型了。

5、回顾总结

最后我们再来回顾下整个模型的训练过程总体可以分为3步走

1、定义一个假设函数 y=wx+b

2、为了找到最能拟合现有数据的w和b我们定义了代价函数 Cost(w,b) 这一步的目标是求解代价函数的最小值

3、通过梯度下降法求解代价函数的最优解

其实大部分的机器学习算法的训练模型的过程都可以分成这3个阶段。不同的他们的假设函数和代价函数非常复杂。比如上面我们定义的y=wx+b只能模拟一个直线如果要模拟稍微复杂些的曲线假设函数可能会变成
$$y={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+...+{\theta }_n{x}_n$$
这里面有n个变量需要求解代价函数也会复杂很多不过依然可以用梯度下降法求解。

另外对于求解代价函数的最优解也并非只有梯度下降法这个一个方法还有很多不同的方法。感兴趣的可以自己去了解。

三、衡量一个模型的好坏

模型验证

当一个模型开发出来后我们需要来验证它的好坏。不同的场景有不同的验证标准比如对于线性回归问题我们通常采用均方差和方根均方差来衡量也就是损失函数而对于逻辑回归或分类问题一般采用准确率和召回率的指标。

我们希望模型做的事情就是预测数据因此模型好坏程度说白了就是这个模型对于新数据的预测准确程度。

当我们拥有大量数据时比如多于1w条直接简单的将数据集分为训练集和测试集就可以了。训练集用来训练模型测试集用于验证模型的好坏。当手中的数据较少一般就需要使用交叉验证常用的交叉验证方法也有多种。

1、简单交叉验证

随机将样本分为两部分比如70%的训练集和30%的测试集然后用训练集来训练模型在测试集上验证模型及参数。之后将样本打乱重新选择训练集和测试集继续训练模型以及验证模型。多次之后选择最优的模型和参数。

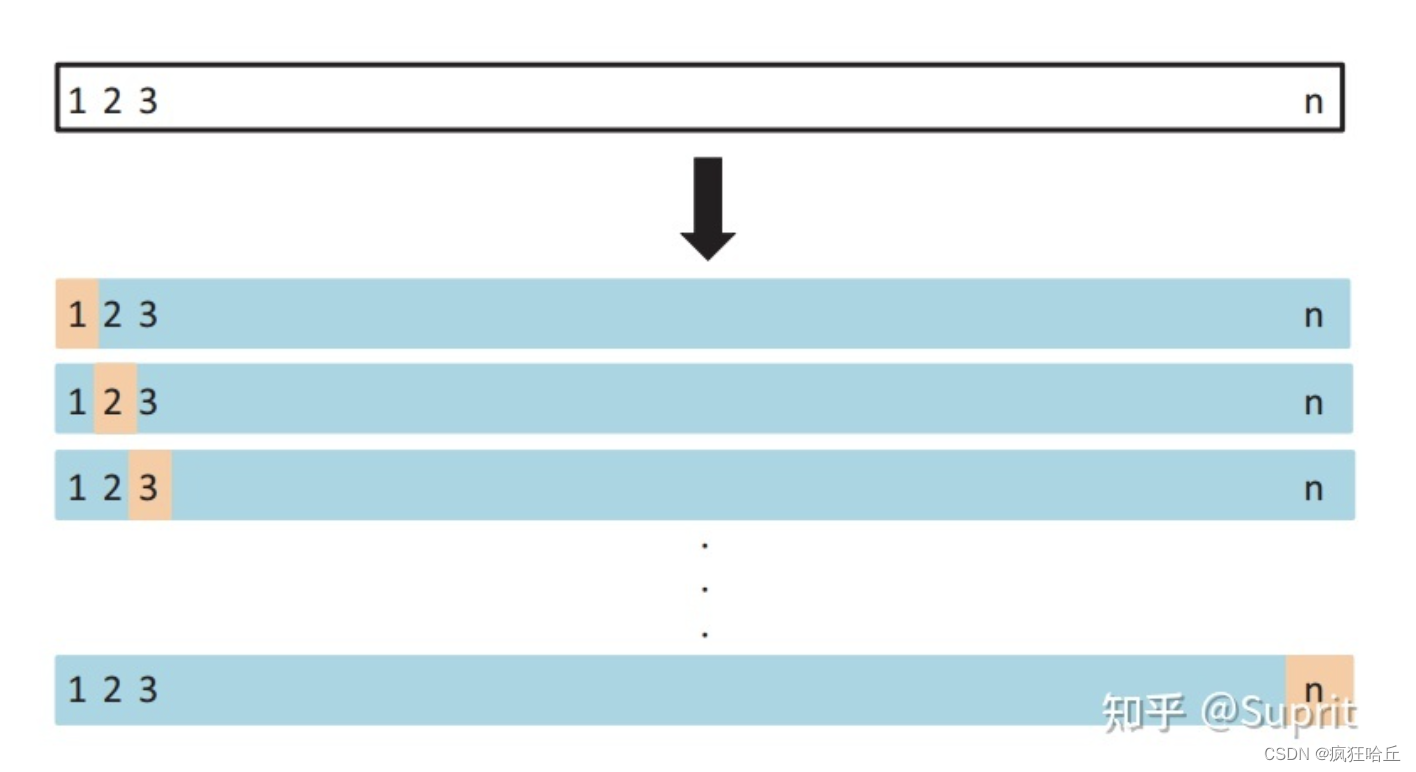
2、K 折交叉验证

将样本划分为K组每次随机选择K-1份作为训练集剩下一份作为测试集。一轮完成之后重新随机选择K-1份来训练数据若干轮后(小于等于K)选择最优的那个模型和参数。

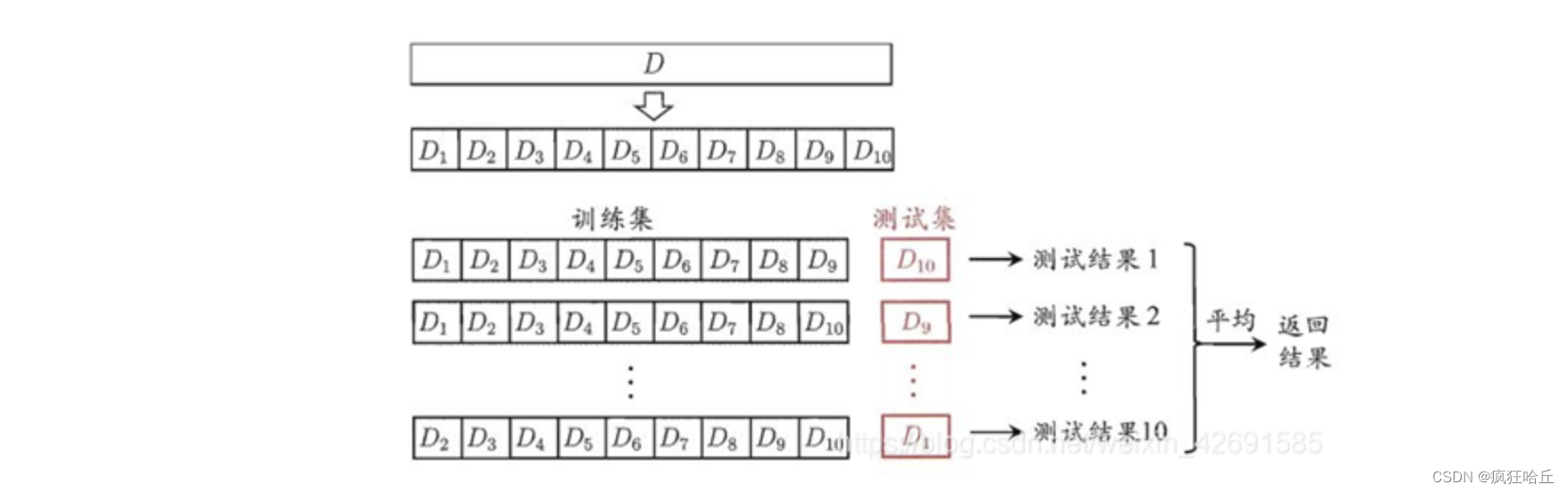
3、留一交叉验证

这种是属于K折交叉验证的特例如果样本数量非常小比如小于50比如样本数量是N。就可以将N-1拿来作为训练数据剩下的一条作为测试数据以验证模型的好坏。并将此步骤重复N次。最后得到效果最好的那个模型。这种验证方法一般用于样本数量非常少的情况下。

过拟合

在机器学习领域有个词叫做过拟合大家可能都有听过。它表示我们训练出来的模型对训练集上的数据有非常好的拟合效果但是对于测试集的数据却无法很好的工作。字面意思其实很简单在实际做模型训练时我们一般都要尽量避免过拟合的情况。

但是大家有没有想过为什么会有这样的情况明明我把训练集的数据都拟合的非常好了由说我不好呢。

我们可以通过一个例子来了解一下这个问题

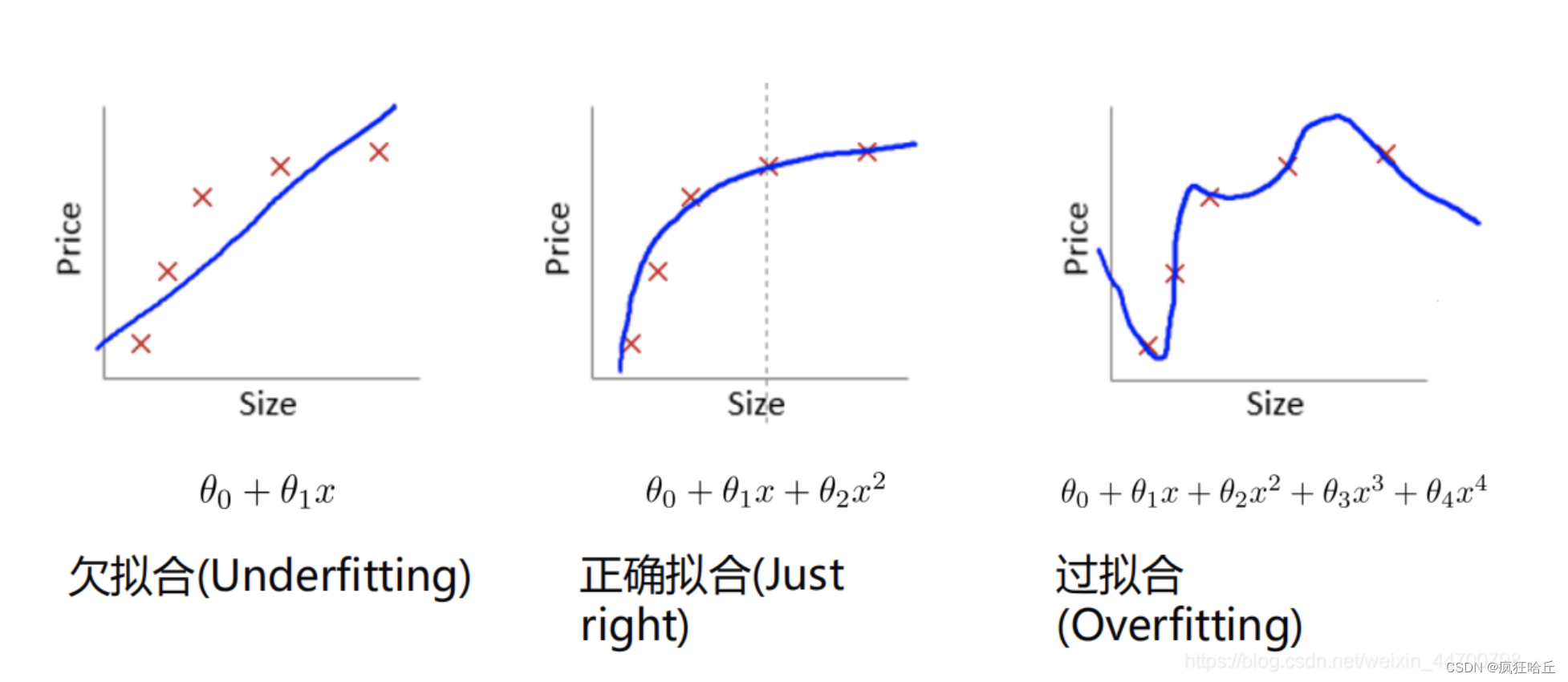
上面这张图中3个曲线拿来训练的数据都是一样的但是训练出来的模型缺相差甚远。其实主要是由于最初定义的假设函数不一样。

对于第一个曲线它定义的假设函数和我们之前举的例子是一样的
$$y={\theta }_0+{\theta }_{1}x$$

很明显它无法很好的拟合训练集的数据更别提之后去预测新的数据了。因此它是欠拟合的。

对于第二个曲线他的假设函数比第一个稍微复杂了一点它需要确定3个参数
$$y={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$$
可以看出最终它训练出来的模型基本可以吻合训练数据(有些许偏差)同时根据我们对这5个点数据的分布观察将来有新的数据它应该也能比较好的拟合。因此这个模型在我们看来是刚好拟合的。

最后一个曲线它的假设函数就复杂了很多需要确定的参数直接达到了5个
$$y={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+{\theta }_4{x}^4$$
然后我们来看一下它训练出来的模型几乎完美吻合训练集上的每一个点比第二个曲线拟合的更好。但是很明显对于未来新的数据它大概率无法很好的拟合。这种现象就是过拟合。

大家可以思考下为什么会有这样的情况。

究其原因主要还是因为第三个曲线的模型太过复杂了。根据奥卡姆剃刀原则simple is more。模型应该是越简单越好复杂的模型可能会导致泛化能力变低当然在简单的同时也要保证能很好的拟合数据比如上面的第一个模型就足够简单但是无法很好的工作。因此在机器学习任务中应该尽量减少模型的复杂度来降低过拟合的风险。

在了解了过拟合问题的根因后我们可能会想该如何解决过拟合问题呢大家可能会想过拟合既然是由于模型太过复杂造成的那么我们在训练模型时尽量让假设函数简单些不就得了。但这样又引入一个新的问题太过简单的假设函数无法很好的拟合数据也就是欠拟合该怎么办

针对这个问题机器学习的大佬们也给出了相应的解决方案正则化。

首先我们还是先给出假设函数为了方便后面解释这里我们用h来代替y表示这个假设函数
$$h({\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+{\theta }_j{x}^4$$

这个假设函数复杂些也没有关系关键在于代价函数再引入正则化之后代价函数会变成
$$Cost({\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4)=\frac{1}{2m}[\sum _{i=0}^m(y_i-h({\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4){)}^2+\lambda \sum _{j=1}^4{\theta }_j^2]$$

和之前的代价函数不同的是这里多了正则项
$$\lambda \sum _{j=1}^4{\theta }_j^2$$

λ为正则化参数是为了平衡代价函数。需要选择合适的值。后面是将θ1、θ2、θ3、θ4的值累加起来注意这里没有θ0因为θ0对应的是x的0次方不会引起模型的复杂化然后和λ相乘。

有了这个正则项之后在计算代价函数的最小值时各个θ的取值就会影响结果。一般而言自然是各个θ的值越接近0就越好。所以正则项也可以理解为惩罚项各个θ越大它的惩罚力度就越大。

如果我们用带正则项的代价函数去训练模型最后可能会发现训练出来的θ3、θ4等于0最终得到的模型刚和曲线2的一致
$$y={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$$
因此通过正则化即使我们一开始给定了一个比较复杂的假设函数依旧可以避免过拟合的现象训练出一个比较好的模型出来。