无理数存在性的几何证明
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
大家知道毕达哥拉斯的名字,是由于那个尽人皆知的定理,这个定理在中国被叫做勾股定理,但很多人不知道以他命名的学派,更不知道这个学派中曾经发生的一个重要事件,这个事件就是无理数的发现。无理数的发现引发了数学上的异常重要风波,它被称为第一次数学危机,而它的发现者也因为破坏了学派创始人的信仰,被残酷的抛入大海。本文准备用图形化的方式,介绍一个例子,来说明无理数存在的合理性。
由于受到当时哲学的影响,毕达哥拉斯学派认为世界的物质是由"原子”构成的,这里的原子并不是我们现代意义上的原子,基于这一看法,它们提出了一条公设.,这个公设断言:
任意两条直线段均有公度
更具体的说,若

与
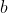
为任意两条直线段的长度,则存在一条直线,其长度为
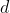
,使得
所以:
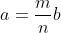
通过公倍操作,总可以有办法,使m,n是正整数,如下图所示:

如果把
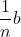
看作单位长度,它就是我们要找到公度长度,n个单位长度就是b,而m个单位长度就是a.
这个过程怎么看怎么像用辗转相除法取最大公约数的过程。注意,这里的整数条件很重要,后面几何证明的时候,要用到这个条件推出矛盾。
也就是说,毕达哥拉斯学派认为:对于任何两个直线段长度,都存在一个长度,在两个线段上都可以放置整数次,所以线段之比可以用整数之比来表示,但是无理数发现者说不,存在不可通约的量,在这种情况下,你找不到一个公度长度量,使两个长度都是公度量的整数倍。
无理数存在的例子:
看下面的等腰直角三角形
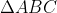
,当然我们现在知道
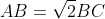
,因为
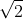
是无理数,所以
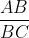
是不可通约量,不能由有理数分式表示,但是现在,我们假设不知道这个前提,也不知道勾股定理,看能推导出什么。
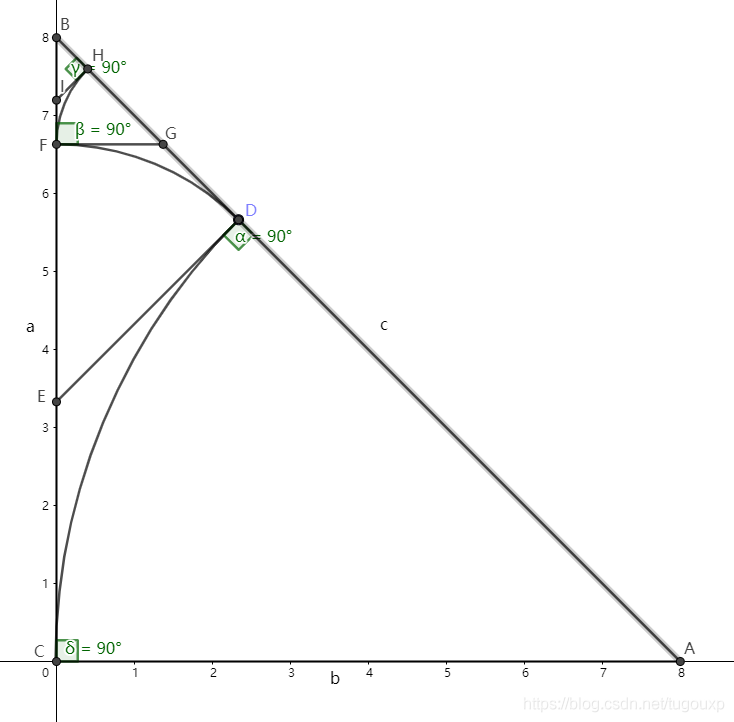
分别表示角对应对边的长度,证明
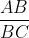
不可通约,也就是证明

不可通约,用反证法,假设存在一个通约量
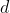
,使
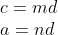
则
如果存在通约量d,不管它是整数还是小数,我们总能找到m,n是正整数,这是一个很重要的条件,后面将用它推导出矛盾。
我们绘制辅助线,以A为圆心,AC为半径做圆,交AB于D点,然后再过D点做AB的垂线,交BC于E.容易证明:
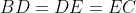
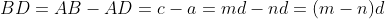
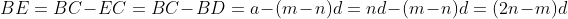
也就是说,如果d是等腰直角三角形
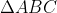
的斜边和直角边的通约量,那么它同样也是等腰直角三角形
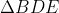
的斜边和直角边的通约量。
同样的辅助线我们可以继续往下画,继续往下推导,由于m,n是正整数,而计算出来的下级等腰直角三角形的边长始终是d的整数被的和差,基于这个原因,会得到一个结论,那就是,如果一直画下去,任意子级的等腰直角三角形的斜边和直角边都有同一个可通约量d.d是所有这些等腰直角三角形的公度。
咦,这个结论肯定是错误的嘛,三角形越来越小,必然会出现三个边都小于d的情况,怎么可能公度一直都是d呢。
而这个结论是我们承认“存在可通约量d"的必然结论,所以,只能说明我们的前提一开始就错了,也就是说,根据排中律,不存在这样的d,使得
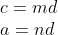
所以,通过绘制等腰直角三角形,我们得到了两条无法通约的线段!
证明的过程很自然,也找不到任何破绽,但是总觉得还是缺乏一点东西,比如,为了证明命题不可通约成立,我们用了反证法,用几何方式构造出矛盾,从而证明了原命题。但是直角三角形有很多种,比如通常用来说明勾股定理成立的直角边3,4,斜边5的直角三角形,它的斜边与直角边之比分别为
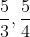
.,就是可以同约的,至少存在通约量1。那问题就来了,同样的证明过程是否能够使用3,4,5边长构成的三角形上,如果同样的证明过程适用于后者,那就是说同一个证明逻辑既可以证明通约,又可以证明不可通约,那证明就有问题。
当然,这个证明没有问题,有问题的是我们对后者的逻辑,现在就看看对于3,4,5的三角形,上面的证明逻辑那里不适用
同样,对于边长比例为3,4,5的三角形,假设通约量d.
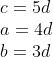
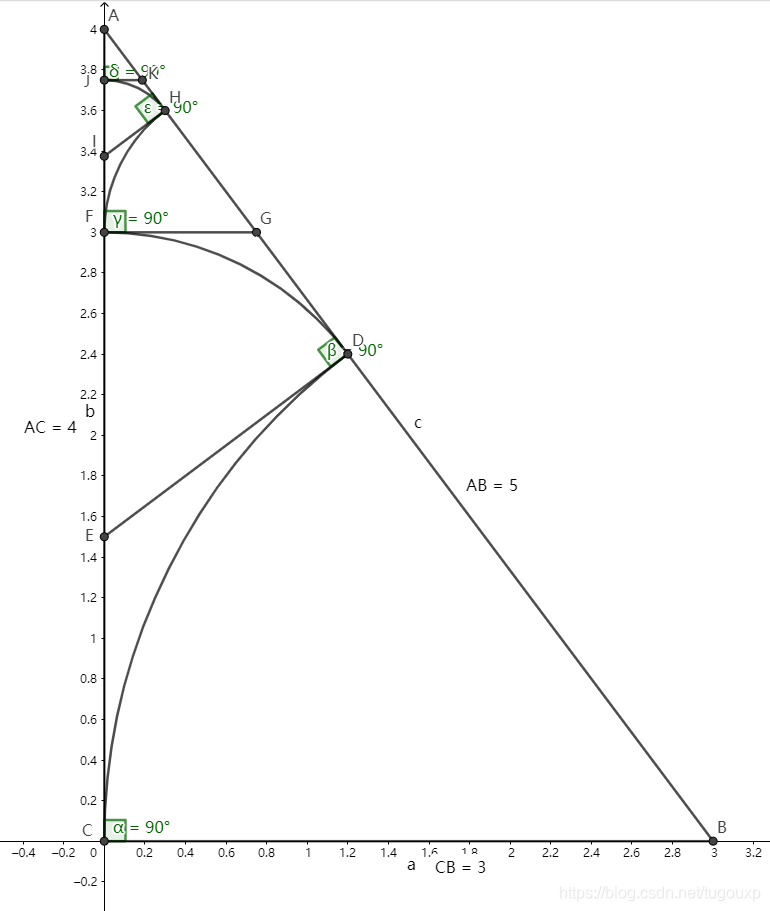
同样的方式,我们绘制辅助线和辅助圆,得到以下结论:
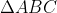
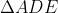
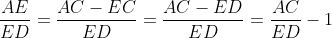
根据相似性:
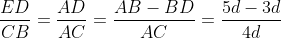
所以,
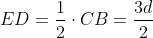
所以,看出来了吗?虽然我们仍然可以像等腰直角三角形那样一直进行下去,可是从第二个直角三角形开始,d的系数已经是不是整数,就是这个根本差异,导致了同样的过程推到不出同样的结论,等腰直角三角形的情况下,在假设成立必然推出腰线始终被控制在d的整数倍,所以矛盾不可避免。
但是对于第二种可以通约的情况,则没有这种限制,边长系数出现了小数,说明我们可以通过对d再抽取一层和系数相乘划归为整数继续进行下去,斜边和直角边仍然是可规约的,只不过这时候通约量变成了
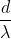
,而不是原来的d了,这样就绕开了矛盾,可以一直画下去而保持通约。
所以,我们消除了疑虑,通过几何图形化方式证明无理数的存在是可行的。
无理数与有理数有一个重大差别:无理数不可能有一个由整数和四则运算组成的表达式表达。有理数有一个有限的表达式,就是整数分式,但无理数没有。无理数与无穷有千丝万缕的联系,当用小数表示时,它是无限不循环的,需要无穷多个位数,包含无穷多的信息,用连分数表示式,是一个无穷的连分式,用级数表示,是无穷多项级数的累加。它与有理数有着本质的不同。
就拿圆周率
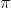
来说,在超级计算机的帮助下,现在已经计算出了
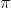
的前一百万亿位,即便如此,我们甚至都不能说“差不多”计算出了
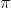
,因为还有“无穷多”的位我们还不知道。
看另一个更漂亮的几何证明:
如果存在最小的整数p,q(约化之后的).
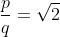
则
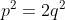
我们用一个边长为p的大正方形内部套着两个边长为q的小正方形为例来说明,注意内部的两个正方形一定有重叠(假如没有重叠,肯定
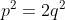
不成立),重叠的深色部分也是一个正方形。则根据初等几何知识,如果
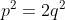
,我们可以得出:
中间深色部分正方形的面积=左下角小正方形面积+右上角小正方形面积=2*两个小正方形任意一个面积
假如中间正方形边长是s,小正方形面积是m.
则
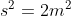
成立。并且s=2q-p, m=p-q都是整数。等等,刚刚不是说了,p,q是最小的满足
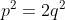
的整数吗?s,m哪里来的? 矛盾!
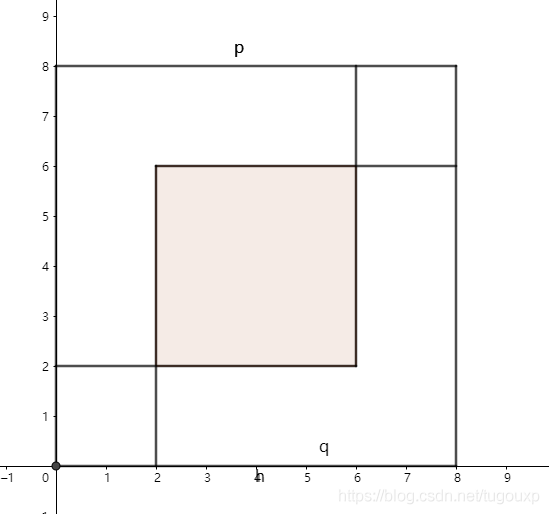
这个证明太完美了!
总结:
也许,这就是我们为数学的美所付出的代价,我们创造了这个虚拟世界(只有在这里,度量才是真正可能的),现在我们必须去面对它所带来的问题,不能够用分数表示的数,就是无理数,英文叫做irrational,不成比例的意思,它们很自然的出现在几何学中,我们必须学会去适应它,正发行的对角线恰好是其边长的根号2倍,这就是我们所知道的关于它的全部,我们只知道这个数的平方是2,我们并不能说出这个值到底是多少,虽然可以粗略的估计它,但是除此之外,我们一无所知。
结束!
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

