详解梯度下降算法
| 阿里云国内75折 回扣 微信号：monov8 |
| 阿里云国际，腾讯云国际，低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号：monov8 飞机：@monov6 |
一、 什么是梯度下降算法
梯度下降法Gradient descent 是一个一阶最优化算法通常也称为最陡下降法 要使用梯度下降法找到一个函数的局部极小值 必须向函数上当前点对应梯度或者是近似梯度的反方向的规定步长距离点进行迭代搜索。 如果相反地向梯度正方向迭代进行搜索则会接近函数的局部极大值点这个过程则被称为梯度上升法 相反则称之为梯度下降法。
1.1 形象理解
梯度下降可以理解为你站在山的某处想要下山此时最快的下山方式就是你环顾四周哪里最陡峭朝哪里下山一直执行这个策略在第N个循环后你就到达了山的最低处
如上图假如为山的纵切面那每次下山一小步经过N次后你便可以到达山底。
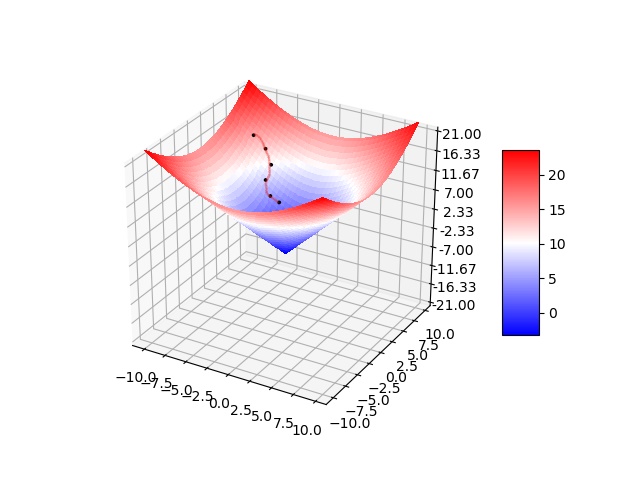
对于3维图像也存在类似步骤使得在N步之后到达山脚下。
1.2 数学理解——微分
在明确何为梯度下降算法后就要对其转化为数学公式或方法以便借助计算机求解进而获取符合我们想要的算法模型对于单个变量的函数如 y = x^2 利用初中二次函数的知识你很快就能理解其存在最小值且最小值为00而为了能够应对复杂函数或者多变量函数如 y(xy=x^2+y^2甚至神经网络中数千维的函数利用公式求解相当复杂而对其进行微分其微分反映的是增量这恰恰是梯度下降算法中我们所需下山最快的方向。
如
d
(
x
2
)
d
(
x
)
=
2
x
\frac{d(x^2) }{d(x)}=2x
d(x)d(x2)=2x
而对于复杂函数如下图y=sinx+cosy此时由于双变量xy的存在仍对其求微此时所求导数为该函数的向量x一个导数y一个导数合起来就是向量如果说单变量函数是指明哪里下山最快那么多变量函数对其微分则是指明哪个方向上下山最快注意此时不再用求导而是用微分是因为导数表示的是比值斜率而微分表示的是增量
以二元函数
z
=
f
(
x
,
y
)
z=f\left ( x,y \right )
z=f(x,y)为例假设其对每个变量都具有连续的一阶偏导数
∂
z
∂
x
\frac{\partial z} {\partial x}
∂x∂z和
∂
z
∂
y
\frac{\partial z} {\partial y}
∂y∂z则这两个偏导数构成的向量
[
∂
z
∂
x
,
∂
z
∂
y
]
\left [ \frac{\partial z} {\partial x},\frac{\partial z} {\partial y} \right ]
[∂x∂z,∂y∂z]即为该二元函数的梯度向量一般记作
∇
f
(
x
,
y
)
\nabla f\left ( x,y \right )
∇f(x,y)。
因此单变量函数中梯度代表的是图像斜率的变化多变量函数中梯度代表的是向量变化最快的地方即最陡峭的方向
1.3 步长学习率 —— a a a
前面一直讨论如何下山最快和如何用数学方法来解决下山最快和下山的方向那么还忽视了一个问题就是下山的步子。当然步子太大容易扯着蛋步子太小下山太慢可能下山都太阳落山了因此需要确定一个步长
a
a
a使得经过合适的步子后能够顺利最快的下山。可能你也能想到最好的方式便是先大步子下山在山的最低处小步不断逼近最低处。但如果在最低处无限逼近那最后的0.000001此时在实际意义来说是无意义的因此同时也需确定某个值使得迭代到某次后判断与设定值的大小若小于则停止循环。
不同步长的比较
小步长
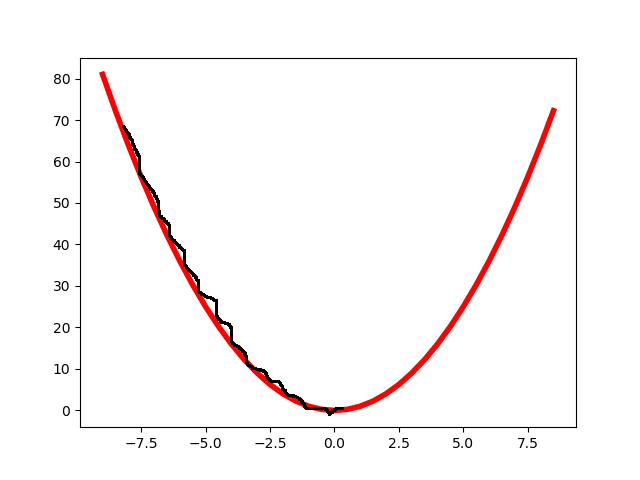小步长表现为计算量大耗时长但比较精准。
大步长
大步长即较大的
a
a
a表现为震荡容易错过最低点计算量相对较小。
注意由于函数凹凸性对于凸函数能够无限逼近其最优解对于非凸函数只能获取局部最优解
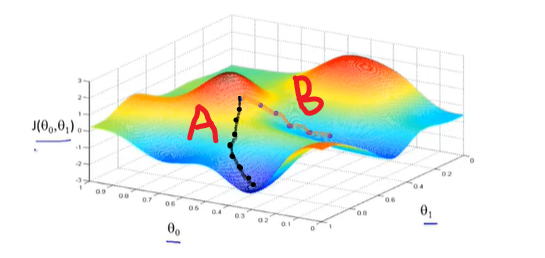
如上图所示对于不同的学习率或步长
α
\alpha
α,其有不同的路径下山路径A和路径B因此存在不同的解这种称之为局部最优解。
1.4 梯度下降算法实现
确定了下降方向和大小后就可以实现梯度下降算法了同样下山前我们假设在一个任意点上Axy方便解释本文统统使用2维坐标更高维的同理那么只需要
A
−
a
Δ
A-a\Delta
A−aΔ
表示每次向下走一小步前面我们已经讨论对于函数而言此时
Δ
\Delta
Δ不能代表方向应该用梯度来表示即
∇
\nabla
∇即
A
−
a
∇
A-a\nabla
A−a∇
计算完一个梯度后需要进行更新点A的坐标Axy循环往复即可求得最优解所以梯度下降的公式为
θ
=
θ
−
α
∗
∇
J
(
θ
)
θ=θ−\alpha∗\nabla J(θ)
θ=θ−α∗∇J(θ)
在明确公式后所以一般的梯度下降算法的步骤为
1、给定待优化连续可微分的函数Jθ学习率或步长a以及一组初始值真实值
2、计算待优化函数梯度
3、更新迭代
4、再次计算新的梯度
5、计算向量的模来判断是否需要终止循环
在python中需要将一维的数字和公式转化为矩阵的形式这能显著提升算法的运行效率和计算时间
假设我们要对简单线性回归进行拟合从高中知识或大学知识我们可得简单线性回归其实就是找出一条直线y=kx+b使得尽可能的穿过多的点如下图
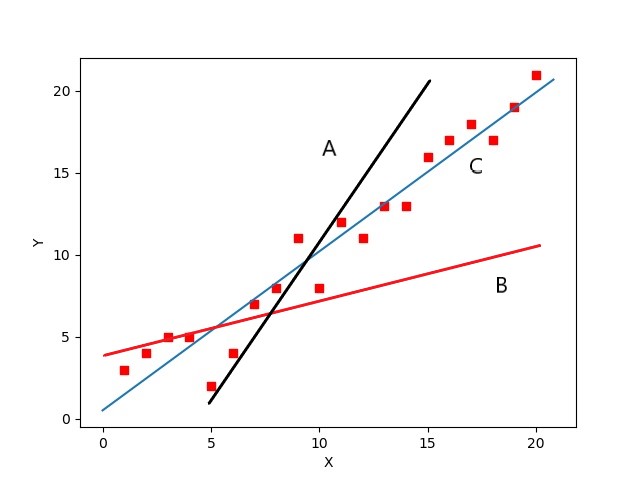
明显直线C为最优的拟合直线则其公式为
J
(
Θ
)
=
1
2
m
∑
i
=
1
n
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J\left ( \Theta \right )=\frac{1}{2m}\sum_{i=1}^{n}\left ( h_{\theta } \left ( x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )^{2}
J(Θ)=2m1i=1∑n(hθ(x(i))−y(i))2
其中
1
2
m
\frac{1}{2m}
2m1是方便求微分对其结果没有影响梯度计算公式
∂
J
(
Θ
)
∂
θ
j
=
1
n
∑
i
=
1
n
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\frac{ \partial J\left ( \Theta \right )}{\partial \theta _{j}}=\frac{1}{n}\sum_{i=1}^{n}\left ( h_{\theta } \left ( x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )x_{j}^{\left (i \right )}
∂θj∂J(Θ)=n1i=1∑n(hθ(x(i))−y(i))xj(i)
迭代公式
θ
=
θ
−
α
∗
∇
J
(
θ
)
θ=θ−\alpha∗\nabla J(θ)
θ=θ−α∗∇J(θ)
1.5 梯度下降算法类型
1.5.1 批量梯度下降算法
前面所讨论中使用的梯度下降算法公式为
∂
J
(
Θ
)
∂
θ
j
=
1
n
∑
i
=
1
n
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\frac{ \partial J\left ( \Theta \right )}{\partial \theta _{j}}=\frac{1}{n}\sum_{i=1}^{n}\left ( h_{\theta } \left ( x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )x_{j}^{\left (i \right )}
∂θj∂J(Θ)=n1i=1∑n(hθ(x(i))−y(i))xj(i)
可以看出计算机会每次从所有数据中计算梯度然后求平均值作为一次迭代的梯度对于高维数据计算量相当大因此把这种梯度下降算法称之为批量梯度下降算法。
1.5.2 随机梯度下降算法
随机梯度下降算法是利用批量梯度下降算法每次计算所有数据的缺点随机抽取某个数据来计算梯度作为该次迭代的梯度梯度计算公式
∂
J
(
Θ
)
∂
θ
j
=
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\frac{\partial J\left ( \Theta \right )}{\partial \theta _{j}}=\left ( h_{\theta }\left ( x^{\left ( i \right )} \right )-y^{\left ( i \right )} \right )x_{j}^{\left ( i \right )}
∂θj∂J(Θ)=(hθ(x(i))−y(i))xj(i)
迭代公式
θ
=
θ
−
α
⋅
▽
θ
J
(
θ
;
x
(
i
)
;
y
(
i
)
)
\theta =\theta -\alpha \cdot \triangledown _{\theta }J\left ( \theta;x^{\left ( i \right )} ;y^{\left ( i \right )} \right )
θ=θ−α⋅▽θJ(θ;x(i);y(i))
由于随机选取某个点省略了求和和求平均的过程降低了计算复杂度提升了计算速度但由于随机选取的原因存在较大的震荡性。
1.5.3 小批量梯度下降算法
小批量梯度下降算法是综合了批量梯度下降算法和随机梯度下降算法的优缺点随机选取样本中的一部分数据梯度计算公式
∂
J
(
Θ
)
∂
θ
j
=
1
k
∑
i
i
+
k
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\frac{\partial J\left ( \Theta \right ) }{\partial \theta _{j}}=\frac{1}{k}\sum_{i}^{i+k}\left ( h_{\theta } \left ( x^{\left ( i \right )}\right )-y^{\left ( i \right )} \right )x_{j}^{\left (i \right )}
∂θj∂J(Θ)=k1i∑i+k(hθ(x(i))−y(i))xj(i)
迭代公式
θ
=
θ
−
α
⋅
▽
θ
J
(
θ
;
x
(
i
:
i
+
k
)
;
y
(
i
:
i
+
k
)
)
\theta =\theta -\alpha \cdot \triangledown _{\theta }J\left ( \theta ;x^{\left ( i:i+k \right )};y^{\left ( i:i+k \right )} \right )
θ=θ−α⋅▽θJ(θ;x(i:i+k);y(i:i+k))
通常最常用的也是小批量梯度下降算法计算速度快收敛稳定。
| 阿里云国内75折 回扣 微信号：monov8 |
| 阿里云国际，腾讯云国际，低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号：monov8 飞机：@monov6 |