【ABAQUS模态动力学】Composite&abaqus 预应力模态分析&输出单元刚度矩阵

阿里云国内75折回扣微信号：monov8

阿里云国际，腾讯云国际，低至75折。AWS 93折免费开户实名账号代冲值优惠多多微信号：monov8 飞机：@monov6

我的主页s

博客园文章链接

https://www.cnblogs.com/aksoam/p/17079348.html

参考

1. 什么是模态分析

模态分析是指求解多自由度系统的模态振型及振动频率的过程。模态分析可简单地分为自由模态分析和约束模态分析。

自由模态分析不加任何约束进行求解会出现前六阶0模态
约束模态分析施加完整的约束模型不会出现刚体模态
还可以分类为
预应力模态典型例子吉他琴弦
干模态分析(空气中)
湿模态分析流体耦合作用不可忽略

2. 单自由度系统振幅和固有频率的求解

模态分析的本质上是求解一定条件下的结构动力学方程。
这是完整的动力学方程

$\tag{1}$

模态分析时假设整体结构处于自由振动状态即 $f (t) = 0$ 并且结构阻你忽略不计, $C = 0$ ,则(1)变为以下公式

$\tag{2}$

对于单自由度系统u是标量而对N自由度系统来说u是一个N x 1的列向量.

2.1 单自由度无阻尼系统的自由振动

最简单的单自由度系统是弹簧-质量块系统

从上可以看出质量块被简化为了一个刚体。方程 $mg-k\delta_{st}=0$ 中影响求解结果的因素只有1质量m2弹簧刚度k;

将单自由度的线性系统无阻尼系统的微分方程写成广义坐标的标准形式

等效质量和等效刚度的求解不讨论(我不会)

广义坐标的定义

以上也是一个模态分析求振型和固有频率的过程。

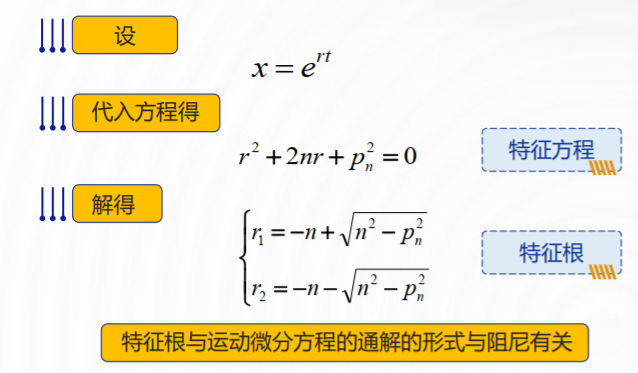
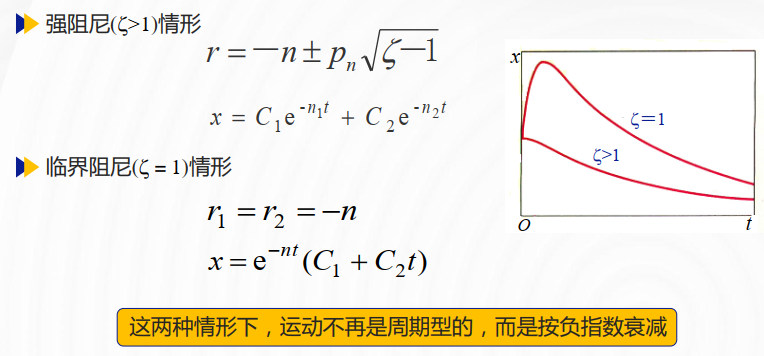
2.2 单自由度有阻尼系统的自由振动

在实际物理模型中阻尼总是存在的。

在这里插入图片描述

3. 从公式推导理解振型和固有频率的概念

之前分析的是单自由度的质量-弹簧-粘壶系统。现在分析多自由度系统。n自由度系统自由振动的微分方程组为

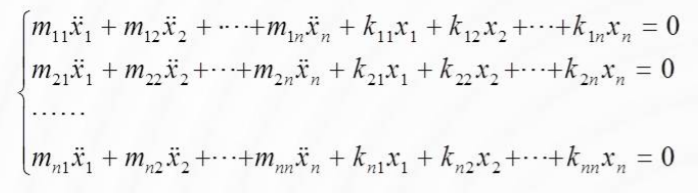
写成矩阵形式为
$\boldsymbol{M} \ddot{x}+\boldsymbol{K} \boldsymbol{x}=0 \tag{3}$

$x$ 为 $n\times 1$ 的向量.(可以理解为广义坐标)
假设解的形式为

$x_{i}=A_{i} \sin (p t+\varphi) \quad i=1,2,3, \cdots n$

解的矩阵形式

$\boldsymbol{x_{n1}}=\boldsymbol{A_{n1}} \sin (p_{n1} t+\phi_{n1}) \tag{4}$

下标n1表示 n 行 1 列

将方程的解代入系统运动微分方程并消去 $sin(pt+\psi)$ ,得:

$KA-p^{2} M A=0 或 K \boldsymbol{A}=p^{2} M \boldsymbol{A} \tag{5}$

整理后
$(K-p^2M)A=0 \tag{6}$
其中特征矩阵为
$B=K-p^2M \tag{7}$

从 $B A = 0$ 来看 $A$ 为自由度振幅向量( $n\times1$ )显然A不可能为0向量(A要有不全为零的解)那么要使 $B A = 0$ 成立系数行列式必须为0
$|B|=0\Rightarrow |K-p^2M|=0 \tag{8}$

这是关于p^2的n次多项式根据此式(3)可以求出n个固有频率或特征值.因此n自由度系统由n个固有频率(模态)

根据公式(5)左乘 $A^T$ 后
$A^T K {A}=p^{2} A^T M{A} \tag{9}$

因为系统的质量矩阵M是正定的刚度矩阵K是半正定或正定的有
$A^T K {A}>=0;A^T M{A}>0$
因此
$p^2=\frac{A^T K {A}}{A^T M{A}} >=0 \tag{10}$

频率方程中所有的固有频率值都是实数并且是正数或为零。刚度矩阵为正定的称之为正定系统对应于正定系统的固有频率值是正的刚度矩阵为半正定的称之为半正定系统对应于半正定系统的固有频率值是正数或为零。

一般来说振动系统的个固有频率的值互不相等重根除外。将各个固有
频率按照由小到大的顺序排列为
$\tag{11}$
最低阶固有频率称为第一阶固有频率或称基频然后依次称为第二阶、第三阶固有频率等。

将频率值带入以下方程
$(K-p^2M)A=0 \tag{12}$
上式是一个n行线性方程组未知数个数为n每一个 $p_i$ 可以求得一个对应的振幅向量 $A^{(i)}$ n行1列满足条件
$(K-p_i^2M)A^{(i)}=0 \tag{13}$

$K 、 M$ 都是n行n列的矩阵 $p$ 为标量。 $A^i$ 为对应于 $p_i$ 的特征矢量。它表示系统在以 $p_i$ 的频率作自由振动时各自由度振幅的相对大小称之为第i阶主振型也称固有振型或主模态。

对于任何n自由度振动系统总可以找到n个固有频率和对应的n个主振型

4. Abaqus中的模态分析

ABAQUS可以进行实模态分析和复模态分析也就是
Natural frequency extraction和Complex frequency extraction。前者对应于frequency分析步这是一个线性摄动分析步.能进行特征值提取计算系统的固有频率和相应的振型

根据帮助文档abaqus的特征值提取分析步求解的是无阻尼有限元模型。其固有频率的特征值问题:

$\left(-\omega^{2}M^{M N}+K^{M N}\right)\phi^{N}=0, \tag{14}$

4.1 Abaqus Theory中的描述

结构分析有许多重要领域对于提取系统的特征值至关重要获得其固有振动频率或研究可能与运动不稳定性有关的分支。例如地震事件的结构评估通常基于线性分析使用结构模式直至限制截止频率这通常是取为 33 Hz周期/秒。

一旦模态是可用的他们的正交特性允许结构的线性响应被构造为一些单自由度系统的响应。这为几种响应评估方法开辟了道路这些方法计算成本低廉并提供对结构的有用行为。Abaqus/Standard 中提供了几种这样的方法

数学特征值问题是一个经典的研究领域许多工作一直致力于提供特征值提取方法。威尔金森1965的书提供了一个关于这个问题的优秀纲要。

由有限元模型所产生的特征值问题是一个特殊的情况它们涉及大但通常是窄带矩阵通常只需要少量的特征对。对于许多重要的情况矩阵是对称的。有限元模型的小振动固有模态的特征值问题是

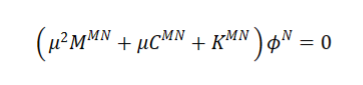
经典矩阵形式

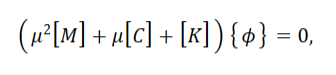
[M]是质量矩阵是对称且正定的 [C]是阻尼矩阵[K]是刚度矩阵;may include large-displacement effects, such as “stress stiffening” (initial stress terms)可能不是正定的或对称的; $\mu$ 是特征值{ $\psi$ }是特征向量(即振动模式)

将abaqus中经典矩阵形式的方程和方程(12)对比可以看出

$\{\psi\}$ 和 $A$ 相当都表示广义坐标下的自由度振幅向量即主振型
$-p^2=\mu^2 \Rightarrow \mu=p i$ 因此 $\mu和p$ 都表示固有频率.

This equation is available immediately from a linear perturbation of the equilibrium equation of the system.

Typically, for symmetric eigenproblems we will also assume that $K$ is positive semidefinite半正定. In this case μ becomes an imaginary eigenvalue, $μ = i ω$ , where ω is the circular frequency, and the eigenvalue problem can be written as

$(-ω^2[M]+[K])⁢{ϕ}=0 \tag{15}$

If the model contains hybrid elements, contact pairs, or contact elements, the system of equations contains Lagrange multipliers and the stiffness matrix [K] becomes indefinite不确定的. However, all the terms of the mass matrix corresponding to the Lagrange multipliers are equal to zero. Therefore, all the eigenvalues are imaginary, and the eigenvalue problem can still be written as above equation