[OpenGL] 视图矩阵(View)矩阵与glm::lookAt函数源码解析
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
一、视图矩阵View矩阵
首先明确视图矩阵的作用在OpenGL的众多坐标系中存在一个世界坐标系和一个摄像机坐标系视图矩阵的作用就是将世界坐标系内的坐标转换成摄像机坐标系内的坐标。
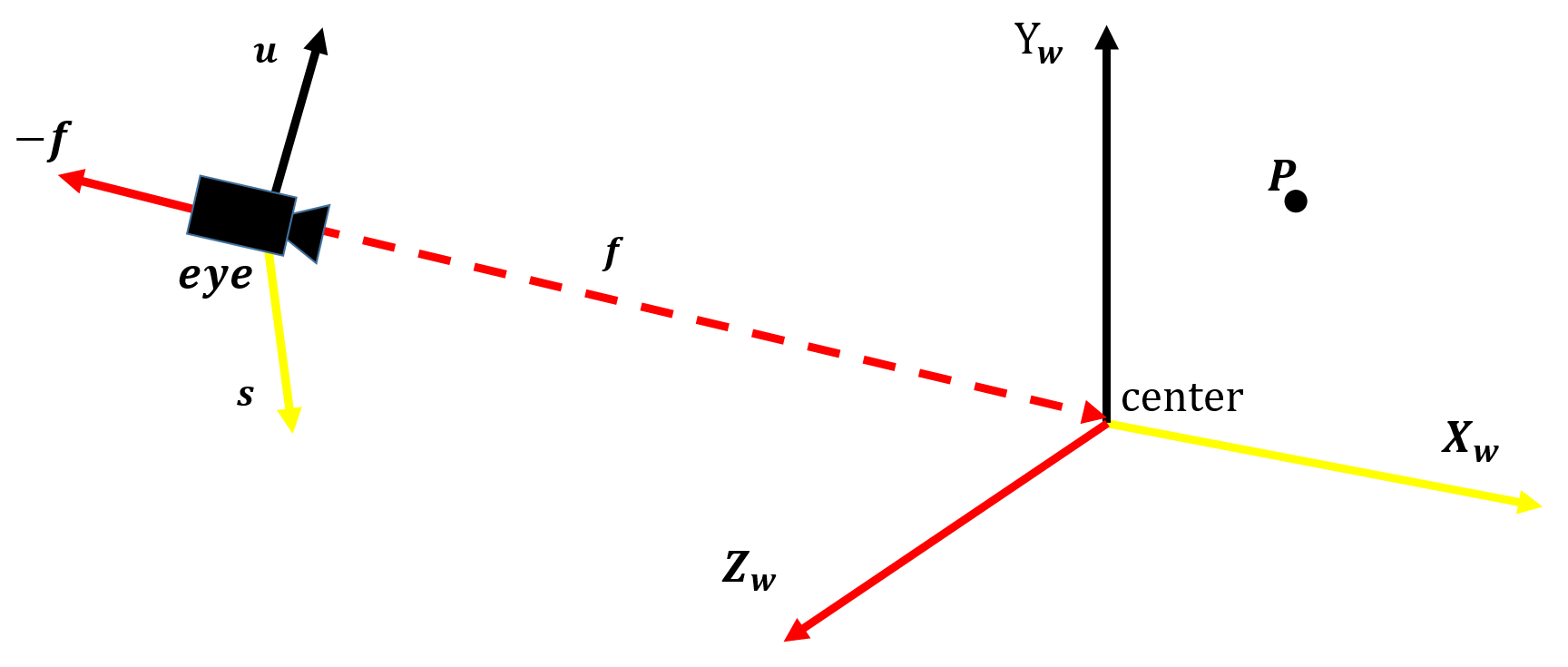
如图空间中存在一个点
P
P
P它在世界坐标系内的坐标为
(
X
w
,
Y
w
,
Z
w
)
(X_w,Y_w,Z_w)
(Xw,Yw,Zw)在摄像机坐标系内的坐标为
(
X
c
,
Y
c
,
Z
c
)
(X_c,Y_c,Z_c)
(Xc,Yc,Zc)在视图矩阵的转换下存在如下等式
[
X
c
Y
c
Z
c
1
]
=
V
i
e
w
[
X
w
Y
w
Z
w
1
]
\begin{bmatrix} X_c \\ Y_c \\ Z_c \\ 1 \\ \end{bmatrix} =View \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \\ \end{bmatrix}
⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤=View⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
二、坐标系的变换与坐标的变换
而上面提到的负责坐标的变换的 V i e w View View矩阵需要明确一下到底是
从世界坐标系变换到摄像机坐标系的旋转平移矩阵
从摄像机坐标系变换到世界坐标系的旋转平移矩阵
两个其中哪一个两个互为逆矩阵
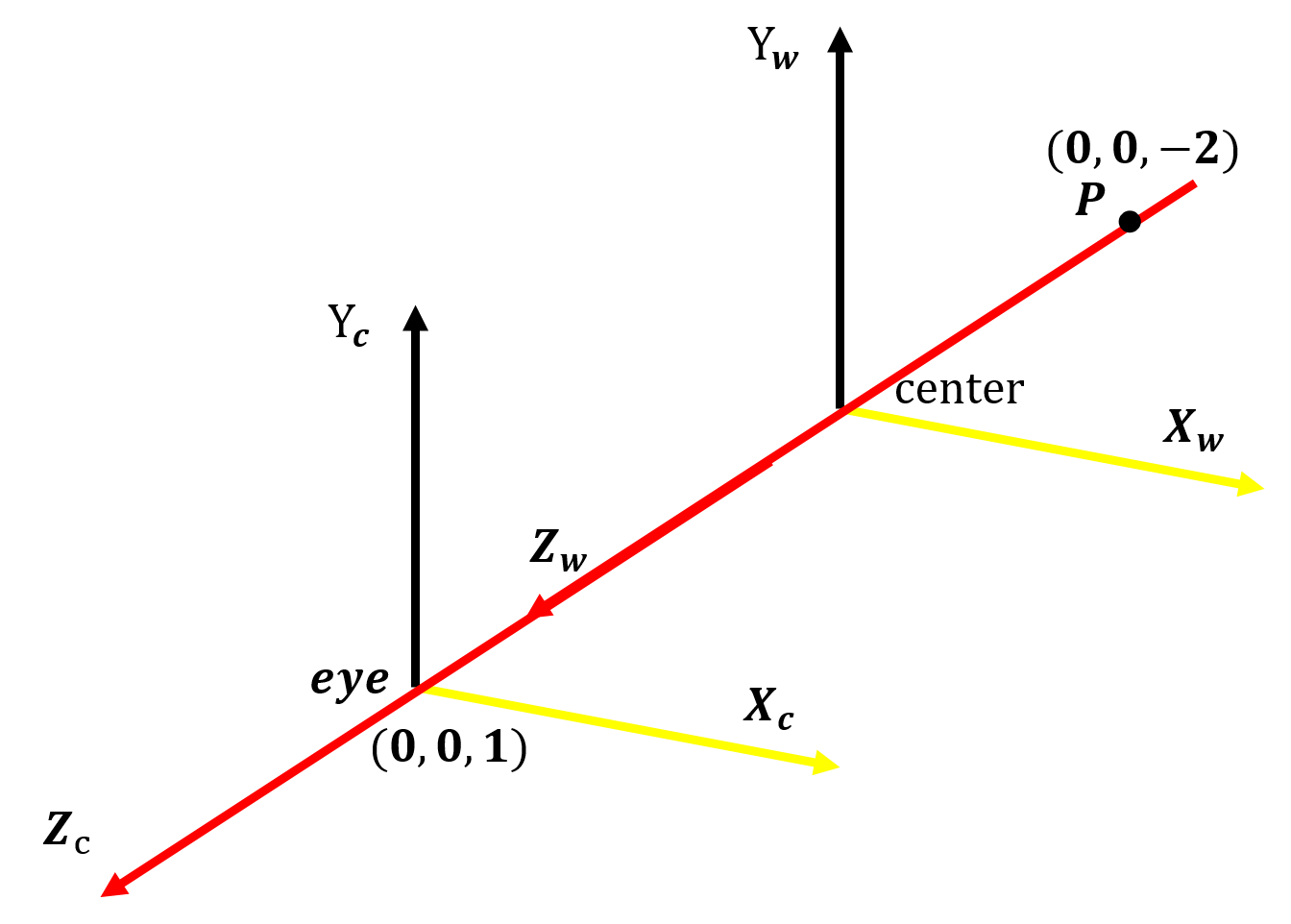
举个简单的例子如下图所示世界坐标系 c e n t e r X w Y w Z w centerX_wY_wZ_w centerXwYwZw内有一点 P w ( 0 , 0 , − 2 ) P_w(0,0,-2) Pw(0,0,−2)摄像机坐标系 e y e X c Y c Z c eyeX_cY_cZ_c eyeXcYcZc各坐标轴与世界坐标系各坐标轴平行即没有旋转变化摄像机坐标系原点位于世界坐标系 ( 0 , 0 , 1 ) (0,0,1) (0,0,1)处。
可以知道 P P P点在摄像机坐标系内的坐标应该为 P c ( 0 , 0 , − 3 ) P_c(0,0,-3) Pc(0,0,−3)
从世界坐标系变换到摄像机坐标系的平移矩阵
T
w
2
c
=
[
1
0
0
0
0
1
0
0
0
0
1
1
0
0
0
1
]
T_{w2c}=\begin{bmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&1&1\\ 0&0&0&1 \end{bmatrix}
Tw2c=⎣⎢⎢⎡1000010000100011⎦⎥⎥⎤
从摄像机坐标系变换到世界坐标系的平移矩阵
T
c
2
w
=
[
1
0
0
0
0
1
0
0
0
0
1
−
1
0
0
0
1
]
T_{c2w}=\begin{bmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&1&-1\\ 0&0&0&1 \end{bmatrix}
Tc2w=⎣⎢⎢⎡10000100001000−11⎦⎥⎥⎤
可以看到
P
w
P_w
Pw到
P
c
P_c
Pc的坐标变换矩阵
V
i
e
w
View
View
P
c
=
V
i
e
w
P
w
=
[
1
0
0
0
0
1
0
0
0
0
1
−
1
0
0
0
1
]
P
w
=
T
c
2
w
P
w
P_c=ViewP_w=\begin{bmatrix}1&0&0&0\\ 0&1&0&0\\ 0&0&1&-1\\ 0&0&0&1 \end{bmatrix}P_w=T_{c2w}P_w
Pc=ViewPw=⎣⎢⎢⎡10000100001000−11⎦⎥⎥⎤Pw=Tc2wPw
简便记忆方法两个相邻的w抵消剩下个c

通俗地来说坐标变化过程可以这样理解将摄像机坐标系经过旋转平移矩阵
(
R
c
2
w
T
c
2
w
)
(R_{c2w}T_{c2w})
(Rc2wTc2w)变化到与世界坐标系重合并且将世界坐标系内原有的顶点坐标做出同样的变换得到的就是那些顶点位于摄像机坐标系内的坐标
因此
V
i
e
w
=
R
c
2
w
T
c
2
w
=
(
R
w
2
c
T
w
2
c
)
−
1
View=R_{c2w}T_{c2w}=(R_{w2c}T_{w2c})^{-1}
View=Rc2wTc2w=(Rw2cTw2c)−1
三、视图矩阵推导
由摄像机坐标系变换到世界坐标系的旋转平移矩阵比较难求但由世界坐标系变换到摄像机坐标系的旋转平移矩阵是非常好求的而这两个矩阵又是互为逆矩阵的关系所以从求解由世界坐标系变换到摄像机坐标系的旋转平移矩阵入手
如图所示摄像机位于世界坐标系中 e y e eye eye 位置并在该位置形成了自己的坐标系要推导视图矩阵需要知道世界坐标系 c e n t e r X w Y w Z w centerX_wY_wZ_w centerXwYwZw是如何变换经过怎样的平移和旋转成为摄像机坐标系 e y e s u ( − f ) eye~s~u~(-f) eye s u (−f)的。
首先是比较简单的旋转变换由于所有向量都是单位向量的形式将世界坐标系旋转到与摄像机坐标系的角度相同所用到的旋转矩阵 R w 2 c R_{w2c} Rw2c可以比较直接地写出来
R w 2 c = [ s x u x − f x 0 s y u y − f y 0 s z u z − f z 0 0 0 0 1 ] R_{w2c}=\begin{bmatrix} s_x&u_x&-f_x&0 \\ s_y&u_y&-f_y&0 \\ s_z&u_z&-f_z&0 \\ 0&0&0&1 \\ \end{bmatrix} Rw2c=⎣⎢⎢⎡sxsysz0uxuyuz0−fx−fy−fz00001⎦⎥⎥⎤
记录一下为什么可以直接写出来吧世界坐标系由三个单位向量组成可以看作一组基旋转后得到的摄像机坐标系可以看作由另外三个单位向量组成即另外一组基。
空间中同一个向量
P
P
P可以由一组基
[
e
1
,
e
2
,
e
3
]
[e_1,e_2,e_3]
[e1,e2,e3]的线性组合表示也可以由另一组基
[
e
1
′
,
e
2
′
,
e
3
′
]
[e_1',e_2',e_3']
[e1′,e2′,e3′]的线性组合表示
P
=
a
1
e
1
+
a
2
e
2
+
a
3
e
3
=
a
1
′
e
1
′
+
a
2
′
e
2
′
+
a
3
′
e
3
′
P=a_1e_1+a_2e_2+a_3e_3=a_1'e_1'+a_2'e_2'+a_3'e_3'
P=a1e1+a2e2+a3e3=a1′e1′+a2′e2′+a3′e3′
其中
a
1
,
a
2
,
a
3
a_1,a_2,a_3
a1,a2,a3便可以认为是向量
P
P
P在由基
[
e
1
,
e
2
,
e
3
]
[e_1,e_2,e_3]
[e1,e2,e3]组成的坐标系内的坐标
a
1
′
,
a
2
′
,
a
3
′
a_1',a_2',a_3'
a1′,a2′,a3′同理。
写成矩阵形式
[
e
1
e
2
e
3
]
[
a
1
a
2
a
3
]
=
[
e
1
′
e
2
′
e
3
′
]
[
a
1
′
a
2
′
a
3
′
]
\begin{bmatrix} e_1&e_2&e_3 \end{bmatrix}\begin{bmatrix} a_1\\a_2\\a_3 \end{bmatrix}=\begin{bmatrix} e_1'&e_2'&e_3' \end{bmatrix}\begin{bmatrix} a_1'\\a_2'\\a_3' \end{bmatrix}
[e1e2e3]⎣⎡a1a2a3⎦⎤=[e1′e2′e3′]⎣⎡a1′a2′a3′⎦⎤
假设由基
[
e
1
,
e
2
,
e
3
]
[e_1,e_2,e_3]
[e1,e2,e3]组成的坐标系就是世界坐标系其中
e
1
=
(
1
,
0
,
0
)
T
e
2
=
(
0
,
1
,
0
)
T
e
3
=
(
0
,
0
,
1
)
T
e_1=(1,0,0)^T\\ e_2=(0,1,0)^T\\ e_3=(0,0,1)^T
e1=(1,0,0)Te2=(0,1,0)Te3=(0,0,1)T
由基
[
e
1
′
,
e
2
′
,
e
3
′
]
[e_1',e_2',e_3']
[e1′,e2′,e3′]组成的坐标系就是摄像机坐标系其中
e
1
′
=
(
s
x
,
s
y
,
s
z
)
T
e
2
′
=
(
u
x
,
u
y
,
u
z
)
T
e
3
′
=
(
−
f
x
,
−
f
y
,
−
f
z
)
T
e_1'=(s_x,s_y,s_z)^T\\ e_2'=(u_x,u_y,u_z)^T\\ e_3'=(-f_x,-f_y,-f_z)^T
e1′=(sx,sy,sz)Te2′=(ux,uy,uz)Te3′=(−fx,−fy,−fz)T
于是
[
1
0
0
0
1
0
0
0
1
]
[
a
1
a
2
a
3
]
=
[
s
x
u
x
−
f
x
s
y
u
y
−
f
y
s
z
u
z
−
f
z
]
[
a
1
′
a
2
′
a
3
′
]
\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix} \begin{bmatrix} a_1\\ a_2\\ a_3 \end{bmatrix}=\begin{bmatrix} s_x&u_x&-f_x\\ s_y&u_y&-f_y\\ s_z&u_z&-f_z \end{bmatrix} \begin{bmatrix} a_1'\\ a_2'\\ a_3' \end{bmatrix}
⎣⎡100010001⎦⎤⎣⎡a1a2a3⎦⎤=⎣⎡sxsyszuxuyuz−fx−fy−fz⎦⎤⎣⎡a1′a2′a3′⎦⎤
[
a
1
a
2
a
3
]
=
[
1
0
0
0
1
0
0
0
1
]
T
[
s
x
u
x
−
f
x
s
y
u
y
−
f
y
s
z
u
z
−
f
z
]
[
a
1
′
a
2
′
a
3
′
]
\begin{bmatrix} a_1\\ a_2\\ a_3 \end{bmatrix}=\begin{bmatrix} 1&0&0\\ 0&1&0\\ 0&0&1 \end{bmatrix}^T\begin{bmatrix} s_x&u_x&-f_x\\ s_y&u_y&-f_y\\ s_z&u_z&-f_z \end{bmatrix} \begin{bmatrix} a_1'\\ a_2'\\ a_3' \end{bmatrix}
⎣⎡a1a2a3⎦⎤=⎣⎡100010001⎦⎤T⎣⎡sxsyszuxuyuz−fx−fy−fz⎦⎤⎣⎡a1′a2′a3′⎦⎤
[
a
1
a
2
a
3
]
=
[
s
x
u
x
−
f
x
s
y
u
y
−
f
y
s
z
u
z
−
f
z
]
[
a
1
′
a
2
′
a
3
′
]
\begin{bmatrix} a_1\\ a_2\\ a_3 \end{bmatrix}=\begin{bmatrix} s_x&u_x&-f_x\\ s_y&u_y&-f_y\\ s_z&u_z&-f_z \end{bmatrix} \begin{bmatrix} a_1'\\ a_2'\\ a_3' \end{bmatrix}
⎣⎡a1a2a3⎦⎤=⎣⎡sxsyszuxuyuz−fx−fy−fz⎦⎤⎣⎡a1′a2′a3′⎦⎤
齐次坐标形式
[
a
1
a
2
a
3
1
]
=
[
s
x
u
x
−
f
x
0
s
y
u
y
−
f
y
0
s
z
u
z
−
f
z
0
0
0
0
1
]
[
a
1
′
a
2
′
a
3
′
1
]
\begin{bmatrix} a_1\\ a_2\\ a_3\\ 1 \end{bmatrix}=\begin{bmatrix} s_x&u_x&-f_x&0\\ s_y&u_y&-f_y&0\\ s_z&u_z&-f_z&0\\ 0&0&0&1 \end{bmatrix} \begin{bmatrix} a_1'\\ a_2'\\ a_3'\\ 1 \end{bmatrix}
⎣⎢⎢⎡a1a2a31⎦⎥⎥⎤=⎣⎢⎢⎡sxsysz0uxuyuz0−fx−fy−fz00001⎦⎥⎥⎤⎣⎢⎢⎡a1′a2′a3′1⎦⎥⎥⎤
P
w
=
R
w
2
c
P
c
P_w=R_{w2c}P_c
Pw=Rw2cPc
至于平移变换由于摄像机位置
e
y
e
eye
eye的坐标是
(
e
x
,
e
y
,
e
z
)
(e_x,e_y,e_z)
(ex,ey,ez)所以将世界坐标系原点
(
0
,
0
,
0
)
(0,0,0)
(0,0,0)平移到摄像机坐标系原点
e
y
e
eye
eye所处的位置所用到的平移矩阵
T
w
2
c
T_{w2c}
Tw2c如下
T
w
2
c
=
[
1
0
0
e
x
0
1
0
e
y
0
0
1
e
z
0
0
0
1
]
T_{w2c}=\begin{bmatrix} 1&0&0&e_x \\ 0&1&0&e_y \\ 0&0&1&e_z \\ 0&0&0&1 \\ \end{bmatrix}
Tw2c=⎣⎢⎢⎡100001000010exeyez1⎦⎥⎥⎤
旋转矩阵是正交矩阵因此它的逆矩阵就是它的转置矩阵
R
c
2
w
=
(
R
w
2
c
)
−
1
=
(
R
w
2
c
)
T
=
[
s
x
s
y
s
z
0
u
x
u
y
u
z
0
−
f
x
−
f
y
−
f
z
0
0
0
0
1
]
R_{c2w}=(R_{w2c})^{-1}=(R_{w2c})^T=\begin{bmatrix} s_x&s_y&s_z&0 \\ u_x&u_y&u_z&0 \\ -f_x&-f_y&-f_z&0 \\ 0&0&0&1 \\ \end{bmatrix}
Rc2w=(Rw2c)−1=(Rw2c)T=⎣⎢⎢⎡sxux−fx0syuy−fy0szuz−fz00001⎦⎥⎥⎤
平移矩阵的逆矩阵就是将平移过的量平移回去
T
c
2
w
=
(
T
w
2
c
)
−
1
=
[
1
0
0
−
e
x
0
1
0
−
e
y
0
0
1
−
e
z
0
0
0
1
]
T_{c2w}=(T_{w2c})^{-1}=\begin{bmatrix} 1&0&0&-e_x \\ 0&1&0&-e_y \\ 0&0&1&-e_z \\ 0&0&0&1 \\ \end{bmatrix}
Tc2w=(Tw2c)−1=⎣⎢⎢⎡100001000010−ex−ey−ez1⎦⎥⎥⎤
求得摄像机坐标系变换到世界坐标系的旋转平移矩阵后根据上文的推导求出
V
i
e
w
View
View矩阵
V
i
e
w
=
R
c
2
w
T
c
2
w
=
[
s
x
s
y
s
z
0
u
x
u
y
u
z
0
−
f
x
−
f
y
−
f
z
0
0
0
0
1
]
[
1
0
0
−
e
x
0
1
0
−
e
y
0
0
1
−
e
z
0
0
0
1
]
=
[
s
x
s
y
s
z
−
(
s
⋅
e
y
e
)
u
x
u
y
u
z
−
(
u
⋅
e
y
e
)
−
f
x
−
f
y
−
f
z
f
⋅
e
y
e
0
0
0
1
]
View=R_{c2w}T_{c2w}=\begin{bmatrix} s_x&s_y&s_z&0 \\ u_x&u_y&u_z&0 \\ -f_x&-f_y&-f_z&0 \\ 0&0&0&1 \\ \end{bmatrix}\begin{bmatrix} 1&0&0&-e_x \\ 0&1&0&-e_y \\ 0&0&1&-e_z \\ 0&0&0&1 \\ \end{bmatrix}=\begin{bmatrix} s_x&s_y&s_z&-(s·eye) \\ u_x&u_y&u_z&-(u·eye) \\ -f_x&-f_y&-f_z&f·eye \\ 0&0&0&1 \\ \end{bmatrix}
View=Rc2wTc2w=⎣⎢⎢⎡sxux−fx0syuy−fy0szuz−fz00001⎦⎥⎥⎤⎣⎢⎢⎡100001000010−ex−ey−ez1⎦⎥⎥⎤=⎣⎢⎢⎡sxux−fx0syuy−fy0szuz−fz0−(s⋅eye)−(u⋅eye)f⋅eye1⎦⎥⎥⎤
四、glm::lookAt
经过上述的推导后相信glm::lookAt函数源码是怎么实现的就很清楚了上文的字母特意选用了与源码内相一致的字母。
glm::lookAt(eye, center, up);
glm::lookAt 函数有三个参数eye 表示摄像机所在位置center 表示摄像机要看向的中心点的位置在本文中是世界坐标系原点up 表示摄像机的三个方位向量中的up向量。
函数返回一个 4 × 4 4\times 4 4×4的视图矩阵view矩阵。
glm::lookAt 其实会先判断是左手坐标系还是右手坐标系因为左手坐标系和右手坐标系z轴的指向不同因而最终的运算结果也有差异OpenGL是右手坐标系因此我们来看看 lookAtRH 函数
GLM_FUNC_QUALIFIER mat<4, 4, T, Q> lookAtRH(vec<3, T, Q> const& eye, vec<3, T, Q> const& center, vec<3, T, Q> const& up)
{
vec<3, T, Q> const f(normalize(center - eye));
vec<3, T, Q> const s(normalize(cross(f, up)));
vec<3, T, Q> const u(cross(s, f));
mat<4, 4, T, Q> Result(1);
Result[0][0] = s.x;
Result[1][0] = s.y;
Result[2][0] = s.z;
Result[0][1] = u.x;
Result[1][1] = u.y;
Result[2][1] = u.z;
Result[0][2] =-f.x;
Result[1][2] =-f.y;
Result[2][2] =-f.z;
Result[3][0] =-dot(s, eye);
Result[3][1] =-dot(u, eye);
Result[3][2] = dot(f, eye);
return Result;
}
函数会先求出 f 向量即摄像机朝向。
vec<3, T, Q> const f(normalize(center - eye));
再通过 f × u p f\times up f×up 叉乘的方式求出 s 向量
vec<3, T, Q> const s(normalize(cross(f, up)));
最后通过 s × f s\times f s×f 叉乘的方式求出 u 向量
vec<3, T, Q> const u(cross(s, f));
函数最终得到的
R
e
s
u
l
t
Result
Result也与我们在上文中推导出的
V
i
e
w
View
View矩阵完全一样由于上文的字母特意选用了与源码内相一致的符号所以两个矩阵直接就可以看出是完全一样的。
V
i
e
w
=
[
s
x
s
y
s
z
−
(
s
⋅
e
y
e
)
u
x
u
y
u
z
−
(
u
⋅
e
y
e
)
−
f
x
−
f
y
−
f
z
f
⋅
e
y
e
0
0
0
1
]
View=\begin{bmatrix} s_x&s_y&s_z&-(s·eye) \\ u_x&u_y&u_z&-(u·eye) \\ -f_x&-f_y&-f_z&f·eye \\ 0&0&0&1 \\ \end{bmatrix}
View=⎣⎢⎢⎡sxux−fx0syuy−fy0szuz−fz0−(s⋅eye)−(u⋅eye)f⋅eye1⎦⎥⎥⎤
R
e
s
u
l
t
=
[
s
x
s
y
s
z
−
(
s
⋅
e
y
e
)
u
x
u
y
u
z
−
(
u
⋅
e
y
e
)
−
f
x
−
f
y
−
f
z
f
⋅
e
y
e
0
0
0
1
]
Result=\begin{bmatrix} s_x&s_y&s_z&-(s·eye) \\ u_x&u_y&u_z&-(u·eye) \\ -f_x&-f_y&-f_z&f·eye \\ 0&0&0&1 \\ \end{bmatrix}
Result=⎣⎢⎢⎡sxux−fx0syuy−fy0szuz−fz0−(s⋅eye)−(u⋅eye)f⋅eye1⎦⎥⎥⎤
注意注意注意这是一个比较重要的小细节
glm库储存矩阵元素采用的是列优先的储存方式
所以mat[ i ][ j ]表示的是第 i 列第 j 行元素
这块代码的元素位置以及本文推导的矩阵内的元素位置并没有问题是完全一样的
Result[0][0] = s.x;//0列0行
Result[1][0] = s.y;//1列0行
Result[2][0] = s.z;//2列0行
Result[0][1] = u.x;//0列1行
Result[1][1] = u.y;//1列1行
Result[2][1] = u.z;//2列1行
Result[0][2] =-f.x;//0列2行
Result[1][2] =-f.y;//1列2行
Result[2][2] =-f.z;//2列2行
Result[3][0] =-dot(s, eye);//3列0行
Result[3][1] =-dot(u, eye);//3列1行
Result[3][2] = dot(f, eye);//3列2行
这里创建的是 4 × 4 4\times4 4×4的单位矩阵
mat<4, 4, T, Q> Result(1);
至此视图矩阵的推导以及glm::lookAt函数的实现源码分析完毕。
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

