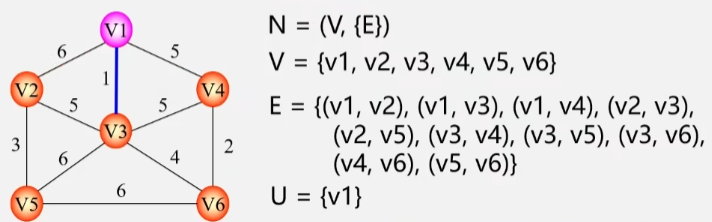其中拓扑排序以及关键路径针对的是一种特殊的图称作有向无环图。

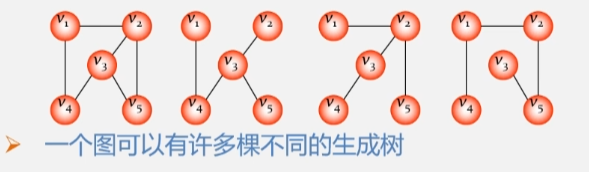
生成树及其构造

生成树

• 图中所有顶点均由边连接在一起但是不存在回路的图。
• 包含无向图 G 所有顶点的极小连通子图。
• 极小连通子图
  • 顶点的边数目在这个连通子图中的数目已经达到最小。
  • 如果在该图中删除任何一条边则子图不再连通如果在该图中增加一条边则图直接构成回路。

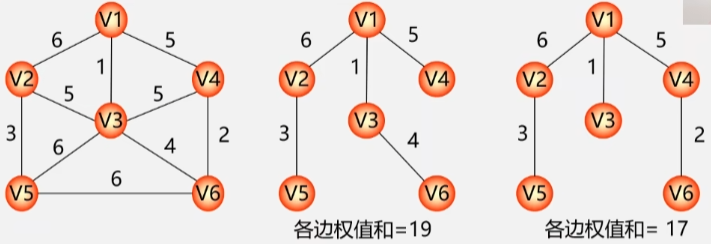
如图右就是由包含图左所有顶点的极小连通子图。

生成树的特点

• 生成树的顶点个数与图的顶点个数相同。

• 生成树是图的极小连通子图去掉一条边则非连通。

• 一个有 n 个顶点的连通图的生成树有 n-1条边。

  • 但是含有 n 个顶点 n-1 条边的图不一定是生成树。
    

• 在生成树中再增加一条边则必然形成回路。

无向图的生成树

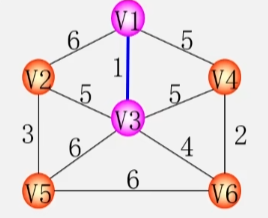
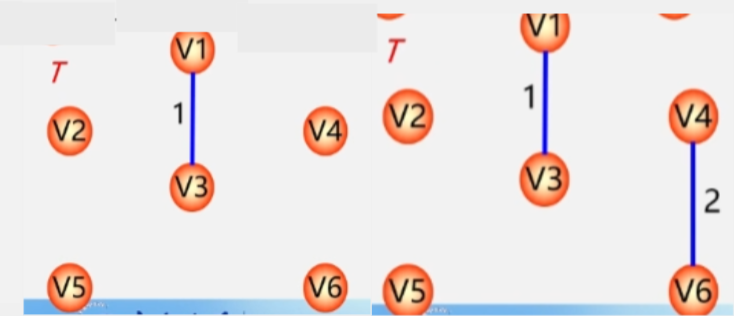
既然一棵生成树需要包含图中所有的顶点那么就对这个图进行遍历。在访问的过程中把走过的这些边加到生成树上就可以得到生成树了。

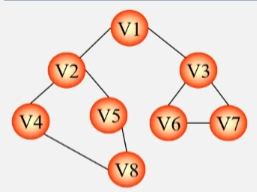
深度优先生成树

• 利用深度优先遍历的方法遍历下图。
• 将图中由蓝颜色的边和所有的顶点构成的图抽出来。
• 这个连通子图就是我们要搞定的生成树了。

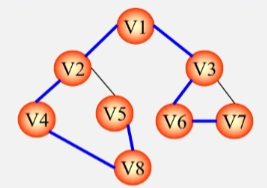
广度优先生成树

1. 从 V1 顶点出发去访问它的所有邻接点 V2 V3。
2. 依次访问 V2 的所有邻接点 V4 V5以及 V3 的邻接点 V6 V7最后访问 V4 的邻接点 V8。
3. 此时根据走过的路径以及所有的顶点也得到了了一棵生成树。

6.6.1 最小生成树

最小生成树及其典型应用

• 通过一个带权值的无向网可以构造多棵不同的生成树。
• 这些生成树当中都包含有 n个顶点和n-1条边。

最小生成树

• 给定一个无向网络在该网的所有生成树中使得各边权值之和最小的那棵生成树称为该网的最小生成树也叫最小代价生成树。

最小生产树的意义

• 将所有的顶点都保持连通边数达到最少且没有回路
• 将所有的顶点连接起来所需要的边的权值最小。

最小生成树的典型用途

• 欲在 n 个城市之间建立通信网则 n 个城市应该铺设 n-1 条线路。
• 但因为每条线路都会有对应的经济成本(边的权值)而 n 个城市最多有 n(n-1) / 2 条线路那么如何选择 n-1 条线路才能使总费用最少？

显然此联通网就是一棵生成树

MST性质

• 构造最小生成树 Minimum Spanning Tree
• 构造最小生成树的算法很多其中多数算法都利用率 MST 的性质。
• 后面要介绍的 Prim算法 和 Kruskal算法 都是使用的MST性质。

MST性质

• 设 N = (V,E) 是一个连通网U 是顶点集 V 的一个非空子集。
• 若边（u,v是一条具有最小权值的边其中 u ∈ Uv ∈ V-U则必定存在一棵包含（u,v的最小生成树。

举个例子

假设有个图 N包含 V 个顶点以及 E 条边。

• U 是顶点 V 的一个非空子集。
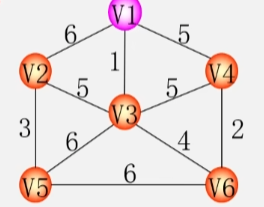
  • 假设现在子集 U 中只有一个顶点 V1。
  • 那么剩下的差集就是所有的顶点减去这个 V1剩下 5 个顶点就在 V-U 这个集合中
• 假设现在存在一条有着最小权值的边这个边是 u 到 v 之间的边。
  • u 在 U 集合中v 则在 V-U 集合中从 u 到 v 中有从 V1 到 V2 、V3 和 V4 三个顶点的边。
  • 其中V1 到 V3 之间的这条边权值最小那么这条边一定会包含在某一棵最小生成树当中。
• 反过来说在构造最小生成树的时候把权值最小的边包含进来

MST性质解释

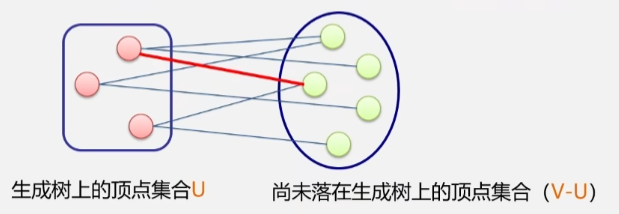
• 在生成树的构造过程中图中 n 个顶点分别属于两个集合
  • 已经落在生成树上的顶点集U。
  • 尚未落在生成树上的顶点集V-U。
• 接下来则应该再所有连通 U 中顶点 V-U 中顶点的边中选取权值最小的边。

1. 现在有不在生成树上的顶点集合 V-U和已经在生成树上的顶点集合 U。

2. 如果从已经在生成树上的顶点到还没有在生成树上的顶点之间存在着很多边。其中有一条边的权值最小。

3. 在构造生成树的时候就将这条边加进去。
   • 前提是生成树不能有回路.
   • 如果出现了回路则继续选择下一条权值最小的边加进生成树。

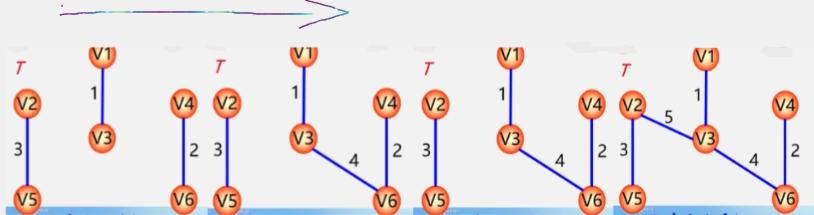
构造最小生成树

构造的最小生成树可能不唯一

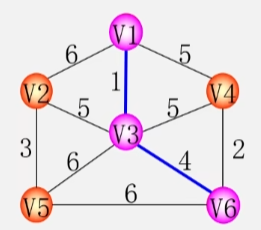
1. Prim(普里姆)算法

算法思想

1. 假设 N = (V,E) 是连通网TE是 N 上最小生成树中边的集合。
   • TE在有 n 个顶点中的图中找到 n-1 条边TE 里存着的就是这 n-1 条边也就是最小生成树中所有的边。
2. 初始令 U = {U0} （从某一个顶点开始构成最小生成树(U0 ∈ V)令边集TE合为空 TE = { }。
   • 这个 U0 就取 V1 来开始构成最小生成树。
   • 采用 MST性质那么 V1 就是 U 集合当中的一个顶点其余顶点为 V-U 集合中的顶点。

3. 在所有 u∈Uv∈V-U 的边 (u,v)∈E 中找一条权值最小的边 (U0,V0)。
4. 将(U0,V0) 这条边 并入边集合 TE同时将这一条边相关联的顶点 V0 并入 U (放到最小生成树中)。
   • 此时最小生成树上的顶点就有两个了。
   • 剩下的 4 个顶点就是 V-U 集合中的顶点了。

5. 接下来继续找已经在生成树上的点和不在生成树上的点之间找一条权值最小的边显然就是 V3 - V6 之间的权值最小。

6. 之后就是以此类推从在树上的所有点和不在树上的所有点之间找一条权值最小的边。
   • 将这条边以及这条边连接的点放入树中（边放入 TE 点放入 U 中。
   • 重复上述操作直至 U=V（U集合包含所有的顶点 为止则 T = (V,TE) 为 N 的最小生成树。

2. Kruskal(克鲁斯卡尔)算法

• 之前说过后 Prim算法 和 Kruskal算法 都是使用的 MST 性质。
• MST 本质上就是贪心算法只不过 Kruskal 算法更贪心而已。

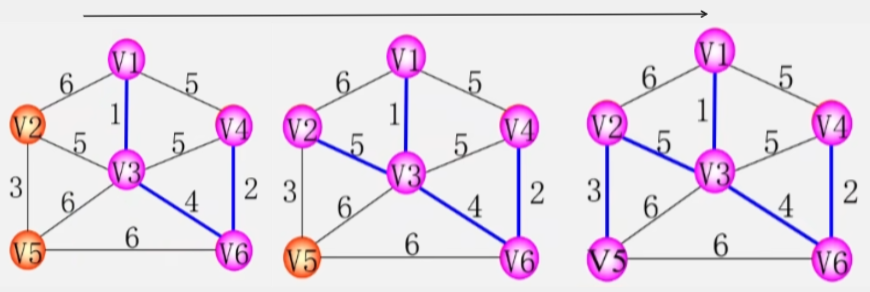
算法思想

1. 设连通网 N = (V,E)令最小生成树初始状态为只有 n 个顶点而无边的非连通图 T=(V,{ })每个顶点自成一个连通分量
   • 人话一开始就直接把连通图上的所有顶点放到最小生成树集合中但不放边进去。

2. 在 E 中选取权值最小的边若该边依附的顶点落在 T 中不同的连通分量撒花姑娘（即不能形成环。则将此边加入到 T 中；否则舍去此边选取下一天权值最小的边。
   • 在连通图中找边的权值最小的边但是每次找最小的比较麻烦所以直接将所有的边按照权值排序排序完之后直接从最小的边开始选。

• 目前权值最小的是 V1 V3之间的边将这条边加入生成树。
• 然后权值最小的变为 V6 V4 之间权值为 2 的边将这条边加入生成树。

3. 以此类推直到 T 中所有顶点都在同一个连通分量上为止（选出了n-1条边为止。
   • 注意当有多个权值相同的边时不能选会让变成环的边比如就不能选V1和V4之间的边否则直接变成环。

此时已经有了 n-1 条边了最小生成树构造完成。

两种算法比较

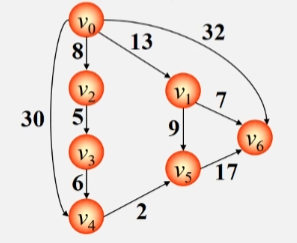
6.6.2 最短路径

最短路径问题

典型用途

• 交通网络的问题从甲地到乙地之间是否有公路连通？
• 在有多条道路的情况下那一条路最短？

交通网络用有权网来表示

• 顶点表示地点。
• 弧表示两个地点有路连通。
• 弧上的权值表示两个地点之间的距离、交通费或路途中所花费的时间等。

如何能够使一个地点到另一个地点的运输时间最短或运费最省这就是一个求两个地点之间的最短路径问题。

问题抽象

• 在有向网中 A 点（起点到达 B 点（终点的多条路径中寻找一条各边权值之和最小的路径即最短路径。
• 最短路径与最小生成树不同路径上不一定包含 n 个顶点也不一定包含 n-1 条边。

第一类问题

• 求两点间最短路径
• 这类问题称作单源最短路径使用==Dijkstra（迪杰斯特拉==算法。

第二类问题

• 某源点到其他各点最短路径
• 这类问题称作所有顶点间的最短路径使用Floyd（弗洛伊德 算法。

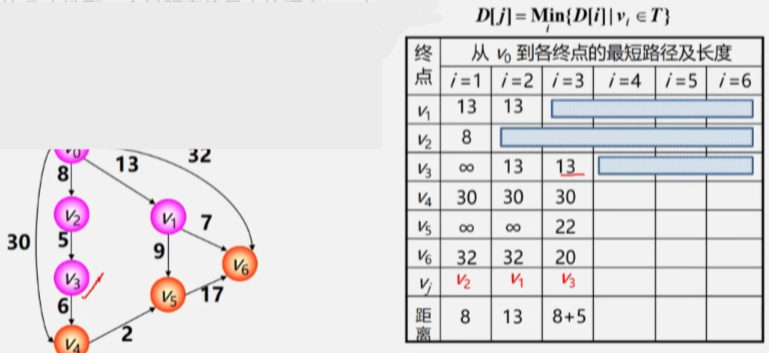
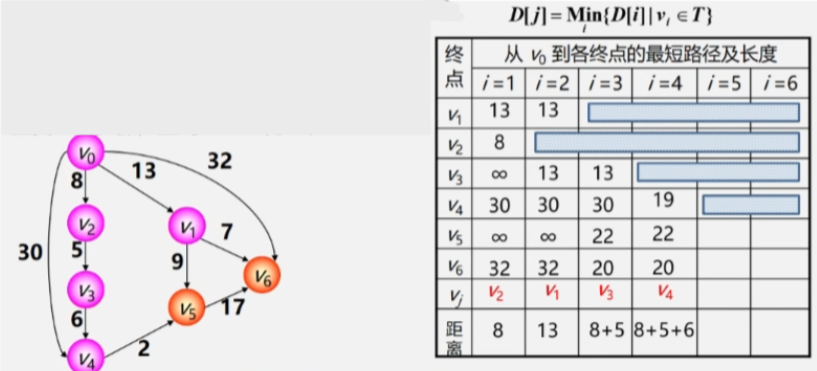
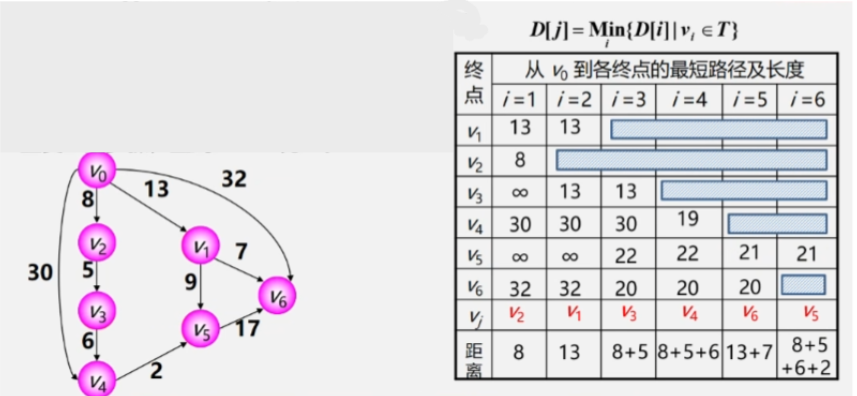
1. Dijkstra(迪杰斯特拉)算法

算法实现

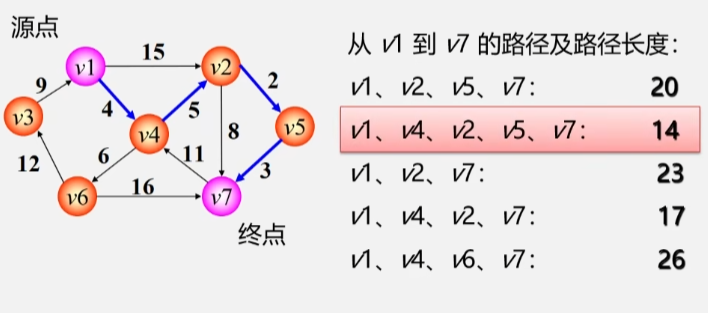
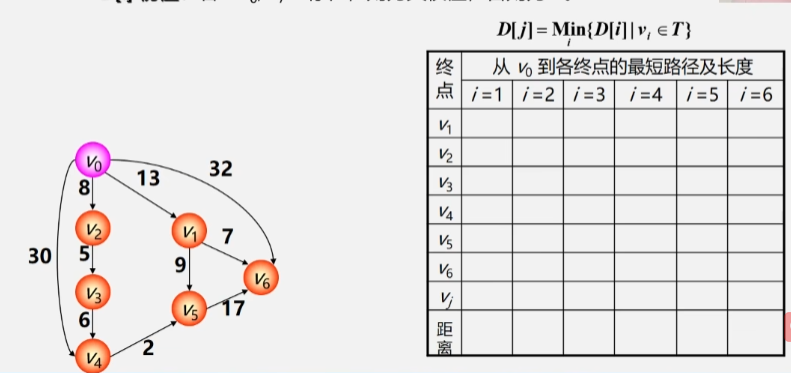
1. 初始化先找出从源点 V0 到各终点 Vk 的直达路径（V0,Vk即通过一条弧到达的路径。
2. 选择从这些路径中找出一条路径长度最短的路径（V0,u。
3. 更新然后对其余各条路径进行适当调整
   • 若在图中存在弧（u,Vk且==（V0,u+（u,Vk<（V0,Vk==则用这条更短路径（V0,u,Vk代替（V0,Vk。
4. 在调整后的各条路径中再找长度最短的路径依次类推。

迪杰斯特拉算法按照路径长度递增次序产生最短路径。

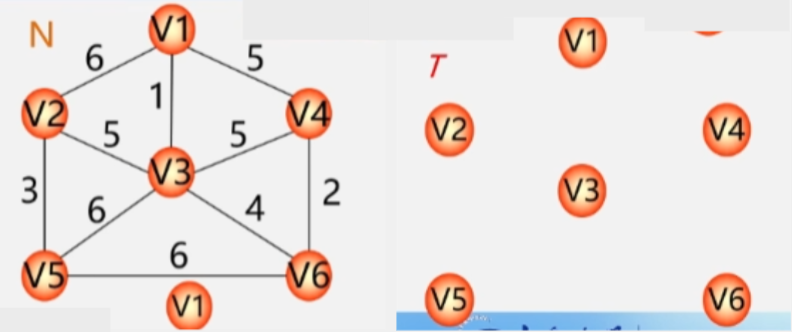
1. 把 V 分成两组

   • S已求出最短路径的顶点的集合。
   • T = V-S尚未确定最短路径的顶点集合。

2. 将 T 中顶点按最短路径递增到的次序加入到 S 中。

   • 保证从源点 V0 到 S 中各定点的最短路径长度都不大于从 V0 到 T 中任何顶点的最短路径长度。
   • 每个顶点对应一个距离值
     • S 中顶点从 V0 到此顶点的最短路径长度。
     • T 中顶点从 V0 到此顶点的只包括 S 中顶点作中间顶点的最短路径长度。

迪杰斯特拉算法步骤

1. 初始时令 S = {V0}T = {其余顶点}。
   • T 中顶点对应的距离值用辅助数组 D 存放。
   • D[i] 初值若 <V0,Vi> 存在（两点间存在弧则为其权值；否则为 ∞。

2. 选择从 T 中选取一个其距离值最小的顶点 Vj 加入 S。
   • 接下来要在这里面找到权值最小的路径与 V0 连接的另一个顶点 V2 加入 Vj。
   • 此时 V2 就加入了已经找到最短路径的顶点集合 S 中了T 中少了个顶点。

3. 更新对 T 中顶点的距离值进行修改若加进 Vj 作为中间顶点从 Vo 到 Vi 的距离值比不加 Vj 的路径要短则修改为此距离值。

   • 人话之后再看从 V0 直接出发到各个顶点的路径以及 V0 经过 V2 再到其他顶点的路径。
   • 看看到其余顶点之间的路径有没有减少如果减少则更新成新的路径。
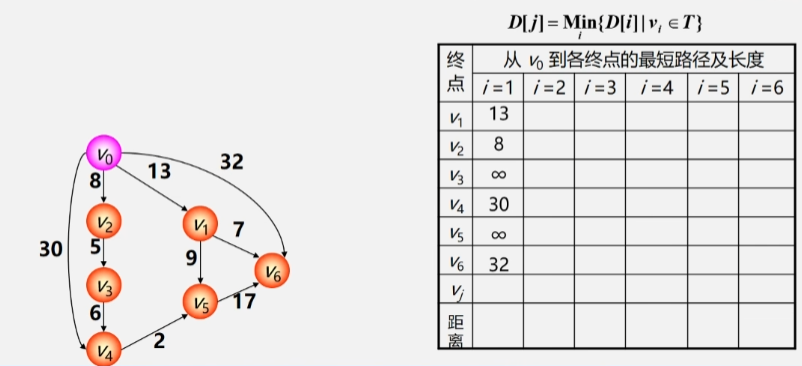
     • V0经过V2到无法抵达V1所以V0到V1之间的路径还是13 没有变化。
     • V0到V2就不用看了它已经找到最短路径了。再看从V0经过V2到V3之间的路径为13。最后V0到V4为30。
     • V0到其余顶点之间即没有弧连着也没有像V2这样的桥梁中转所以全部为∞。
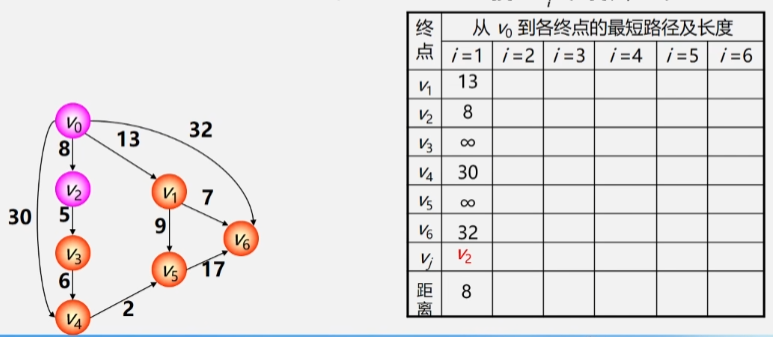
   • 继续挑一个路径与V0之间路径最短的顶点加进 Vj（已找到最短路径的顶点集合中此时 V0-V1已经找到最短路径不再看V1。

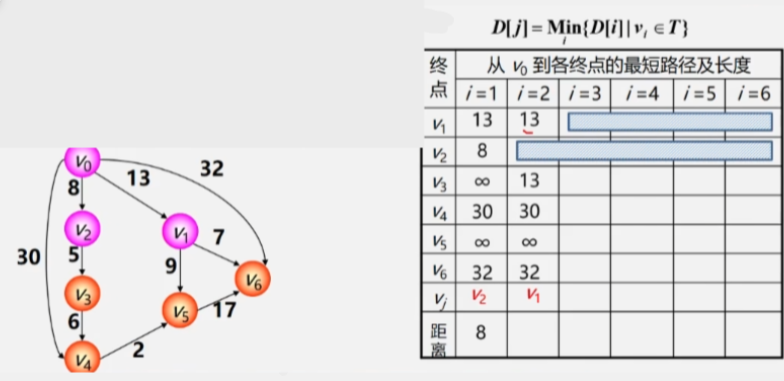
4. 之后 V0 再以 V2、V1作为跳板跑到其他顶点看看到其余顶点间的最短路径有没有变的更短。
   • 将 V3 加入最短路径顶点集之后再以 V3 作为跳板收拾其他顶点。

5. 之后就是依次类推不断更新最短路径以及将 V0 与最短路径之间连着的顶点加进 Vj 。

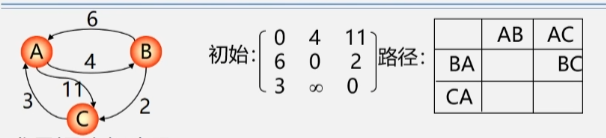
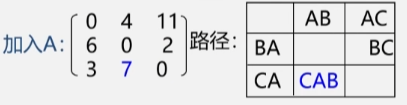
2. Floyd(弗洛伊德)算法

求所有顶点间的最短路径

• 方法一每次以一个顶点为源点重复执行迪杰斯特拉算法 n 次。这个算法的时间复杂度是 O(n³)。
• 方法二Floyd（弗洛伊德算法这个算法要简单很多但是这个算法的时间复杂度任然是 O(n³)。

算法思想

• 逐个顶点试探。
• 从 Vi 到 Vj 的所有可能存在的路径中。
• 选出一条长度最短的路径。

弗洛伊德算法步骤

算法步骤

1. 初始时设置一个 n 阶方阵
   • 令其对角线元素为 0（对角线元素都是到自身的路径不考虑自己和自己之间的路。
   • 两点之间若存在弧 <Vi,Vj>则其对应元素为该弧的权值；否则为 ∞。

2. 逐步试着在原直接路径中增加中间顶点
   • 若加入中间顶点后路径变短则修改之反之维持原值。
   • 直到所有顶点试探完毕算法结束。

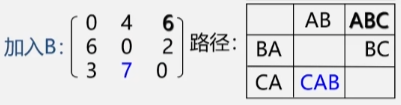
• 加入顶点 A 之后令 C 到 B 之间有了条路对于其余顶点之间的路径并没有影响。

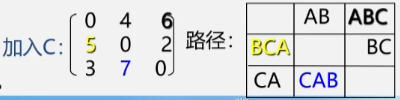
• 加入顶点 B 之后令 A 到 C 之间的最短路径变为了 ABC 这条路径长度为 6 的路径将最短路径修改为这这个对其余顶点间的路径长度无影响。

• 加入顶点 C 之后令 B 到 A 之间的最短路径从 BA 的 6 变为了 BCA 的 5将最短路径修改成这个。

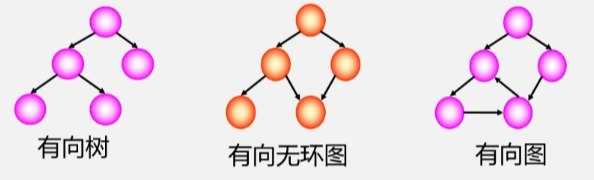
有向无环图及其应用

有向无环图无环的有向图简称 DAG 图。

• 有向无环图常用来描述一个工程或系统的进行过程。（通常把计划、施工、生成、程序流程当成是一个工程
• 一个工程可以分为若干个子工程只要完成了这些子工程（活动就可以使得整个工程的完成。

如何表示这些子工程？

• AOV 网拓扑排序
  • 用一个有向图表示一个工程的各个子工程及其相互制约的关系其中以顶点表示活动以弧表示活动之间的优先制约关系称这种有向图为顶点表示活动的网简称 AOV 网(Activity On Vertex network)。
• AOE 网关键路径
  • 用一个有向图表示一个工程的各个子工程及其相互制约的关系以弧表示活动以顶点表示活动的开始或结束事件称这种有向图为边表示活动的网简称 AOE 网(Activity On Edge)

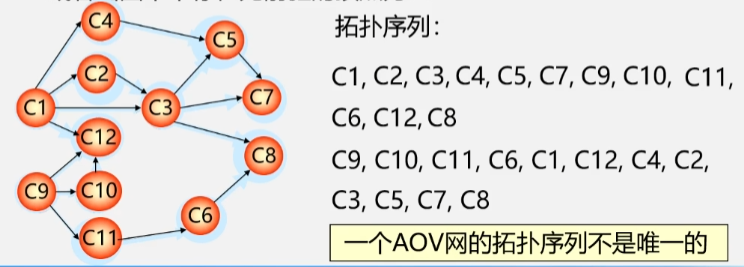
6.6.3 拓扑排序

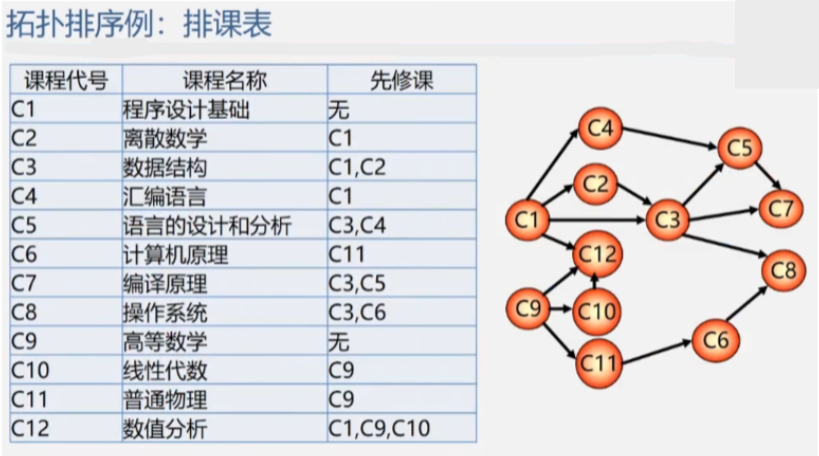
假设现在要安排一份课程表

• 想要学习数据结构这门课的话事先得先学习离散设计和程序设计基础所以数据结构的先修课就是 C1、C2这两门课。

• 再如 C9 的高等数学他没有先修课（前趋但是从图中看C12、C10以及C11都需要先学习过 C9 的课所以 C9 可以当成是这三门课的直接前趋。

• 同样的只有学完了 C9 的数据结构之后才能学习它的后继课程。

• 既然要开设这么些课程但是有着明显前趋后继关系的课程又不能同时进行怎么才能将这些课排在各个学期而且还满足表中的先后关系这个时候就要用到俺们的拓扑排序了。

在有向网中用顶点表示要上的课程用带方向的弧来表示这些课程之间的先后关系

AOV 网的特点

1. 若 从 i 到 j 有一条有向路径则 i 是 j 的前趋；j 是 i 的后继。
   • 如从 C1 到 C5 之间有条有向路径则称 C1 为 C5 的前趋；C5 为 C1 的后继。
2. 若 < i , j > 是网中的有向边则 i 是 j 的直接前趋；j是 i 的直接后继。
   • 如C1 到 C3 之间有一条边则称 C1 为 C3 的直接路径；C3 为 C1 的直接后继。
3. AOV 网中不允许有回路因为如果有回路存在则表明某项活动是以自己为先决条件显然这样不行。
   • 如假设必须学完 C2 才能学习 C1 的课程C1 学完之后才能学 C3C3 学完了才能学 C2。那这就糊涂了该先学那门课捏？

• 问题如何判别 AOV 网中是否存在回路？

拓扑排序的方法

• 在 AOV 网没有回路的情况下我们将全部活动排列成一个线性序列使得 AOV 网中有弧 < i , j > 存在则在这个序列中i 一定排在 j 的前面具有这种性质的线性序列称为拓扑有序序列相应的拓扑有序排序的算法称为拓扑排序。

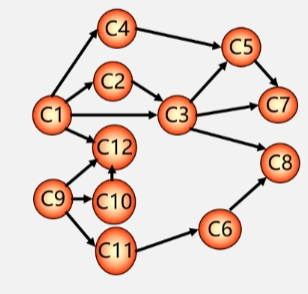
首先先把这个 AOV 网构造出来用顶点来表示学习的课程用顶点之间的有向弧来表示学习的顺序。

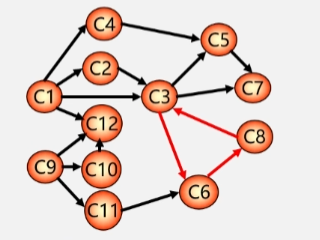
拓扑排序过程

1. 在有向图中选一个没有前趋的顶点且输出它。
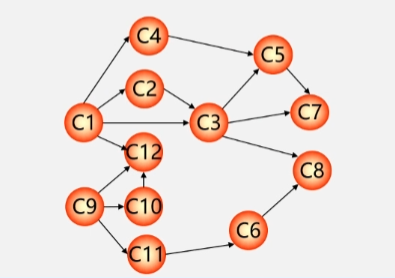
   • 如一开始在图中发现只有C1和C9没有前趋选一个序号最小的 C1 出去。
2. 在图中删除该顶点以及所有从该顶点发射出去的弧。
   • 将 C1 以及它所发射出去的四条弧从图中删除。

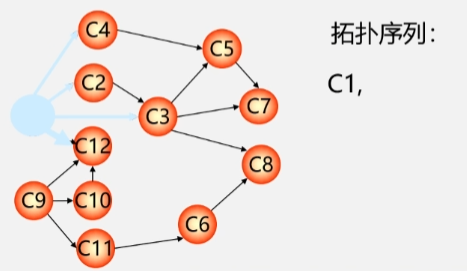
3. 重复（1和（2直到不存在没有前趋的顶点。
   • 拓扑序列的先后顺序不唯一。
   • 但是如果在图中某个顶点是另一个顶点的前趋那么在线性序列中该顶点也必须是另一个顶点的前趋。
     • 如顶点 C3 是 C8 的前趋那么在拓扑序列中C3 的位置也必须在 C8 前面。

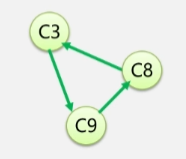
4. 若此时输出的顶点数小于有向图中的顶点数则说明有向图中存在环返之说明输出的顶点序列为一个拓扑序列。

检测 AOV 网中是否存在环

• 对有向图构造其顶点的拓扑有序序列.
• 若网中所有顶点都在它的拓扑有序序列中则该 AOV 网必定不存在环。

简单来说如果一个顶点有环的话即便删掉他的前驱和相关约束关系他自己或者它后继在约束它本身所以他不可能变成那种没有前驱的结点被输出这时拓扑序列的顶点个数必定不等于总顶点个数可能有人会说那为啥后继对它的约束不能被删除呢那是因为后继的前驱是当前结点当当前结点没被删除时后继怎么可能删除呢。

在这三个顶点中找不到没有前趋的顶点这几个顶点没法加到拓扑序列汇总。

6.6.4 关键路径

用AOE网表示工程计划

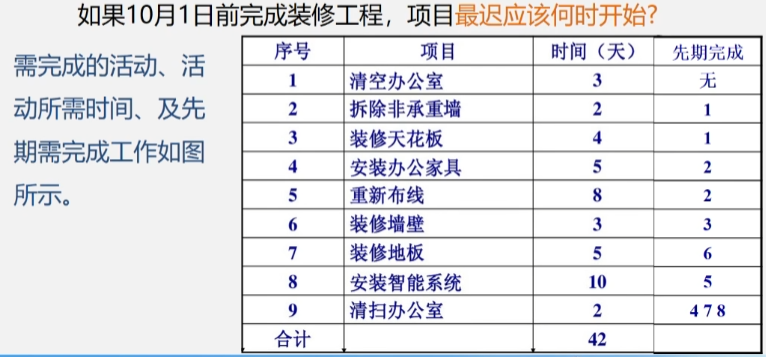
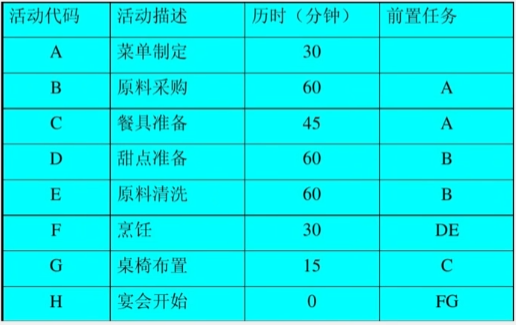
【例1】某项目的任务是对A公司的办公室重新进行装修

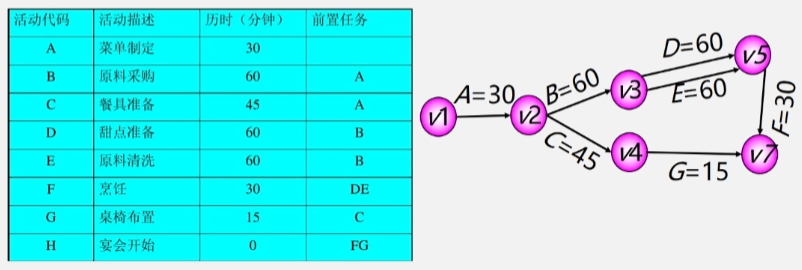
【例2】准备一个小型家庭宴会晚上六点宴会开始最迟机电开始准备？压缩哪项活动时间可以让总时间减少？

• 把工程计划表示为边表示活动的网络即 AOE 网用顶点表示事件弧表示活动弧的权表示互动持续时间。
• 事件（顶点表示在它之前的活动已经完成在它之后的活动可以开始。
  • 如顶点 V2 表示 A 活动结束BC 活动可以开始顶点 V3 表示 活动 B 结束DE 活动可以开始。

求解关键路径

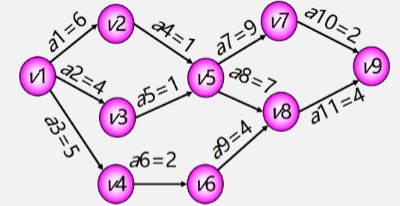
例设一个工程有 11 个活动9 个事件。

• 事件 V1表示整个工程开始（源点入度为 0 的顶点。
• 事件 V9表示整个工程结束（汇点出度为 0 的顶点。

有了这样一个AOE网后现在有两个问题

1. 完成整项工程至少需要多少时间？
   • 关键路径的长度就是整个工程至少需要的时间。
2. 哪些活动是影响工程进度的关键？
   • 关键路径上的这些活动就是影响工程进度的关键。

• 关键路径从源点到汇点路径长度最长的路径。
• 路径长度路径上各活动持续时间（权值之和。

道理很简单就是几个人同时到一个地方集合离得近的到得早离得远的到得晚但只有最晚到的人到了大家才算凑到一块了。

确定关键路径

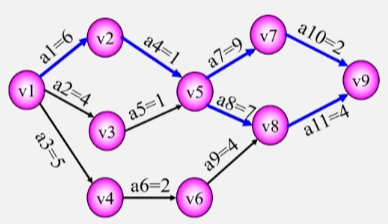
为了确定关键路径需要定义 4 个描述量

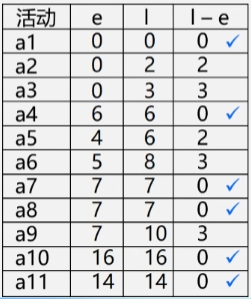
假设所有活动全部完成需要消耗 180 分钟

1. ve(vj)关于顶点的表示事件 vj 的最早发生时间。
   • 如V2 事件表示 a1 最早可以什么时候完成和 a2 最早什么时候可以开始的时间。
   • ve(v1) = 0（事件 v1 不需要等待时间ve(v2) = 30（事件 v2 连着的活动需要等 a1 的 30 完成了之后才能开始
2. vl(vj)关于顶点的表示事件 vj 的最迟发生时间。
   • 如假设所有活动要消耗 180 分钟活动 a7 需要15分钟V4 的 a3 最晚要在第 165 分钟的时候结束活动 a7 最迟要在第 165 分钟开始。
   • 例vl(v4) = 165
3. e(i)表示活动 ai 的最早开始时间
   • 例e(a3) = 30活动 a3 最早能在第30分钟的时候开始。
4. l(i)表示活动 ai 的最晚开始时间。
   • 例l(a3) = 120因为180分钟至少要预留15分钟给a7所以 a3 至少要在这 165 分钟内完成a3要花费45分钟所以活动 a3 最迟要在第 120 分钟开始。

• l(i) - e(i)表示完成活动 ai 的时间余量
  • 例l(3) - e(3) = 90活动 a3 在这 90 分钟内什么时候开始都不会影响进度。
• 关键活动没有时间余量的活动关键路径上的路径即 l(i) = e(i)（即 l(i) - e(i) = 0的活动。
• 由若干个关键活动所组成的路径就是关键路径。

如何找l(i) = e(i) 的关键活动？

设活动 ai 用弧 <j , k> 表示其持续时间记为Wj,k则有

1. e(i) = ve(j)
2. l(i) = vl(k) - Wj,k

如何求 ve(j) 和 vl(j)？

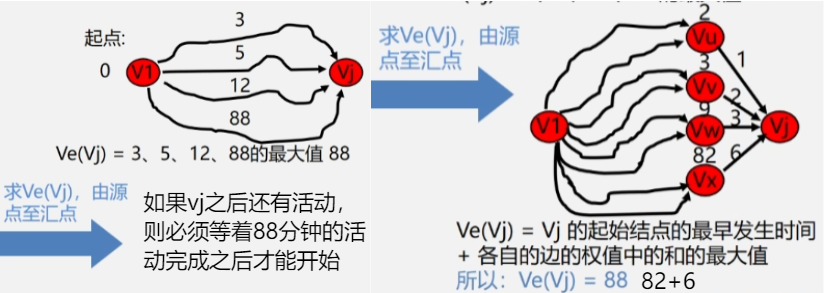
1. 求最早发生时间从 ve(1) = 0开始向前递推
   • ve(j) = Max{ve(i) + Wi,j}< ij > ∈ T2 <= j <= n。其中 T 是所有以 j 为头的弧的集合。
   • 从源点到某个顶点的全部路径中选择路径长度（权值和最大的那条路。
     • 例开始刷牙到结束刷牙根据你出门时间决定你最晚刷牙时间根据你起床决定最早刷牙时间。
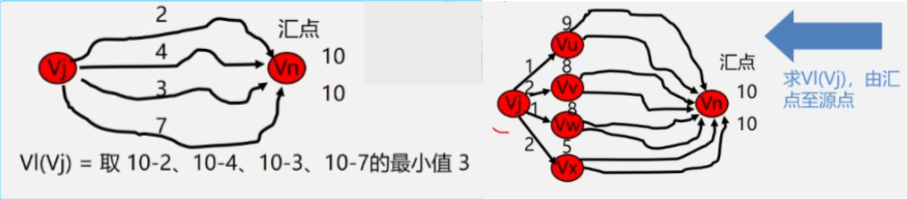
2. 求最晚发生时间从 vl(n) = ve(n) 开始向后递推。
   • vl(i) = Min{vl(j) - Wi,j}< ij > ∈ S1 <= i <= n-1。其中 S 是所有以 i 为尾的弧的集合。
   • Vi 顶点后继的那个顶点Vj的最迟发生时间减去Vi与Vj之间弧的权值。

顶点 vj 的最早发生时间

顶点 vj 的最迟结束时间

• 后面的顶点减去前面的顶点之间的弧的权值取差的最小值

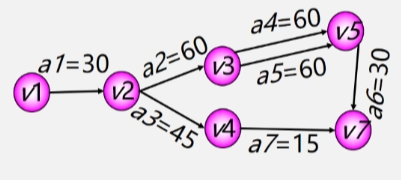
求关键路径步骤

1. 求 ve(i)、vl(j)事件的最早、晚发生时间

2. 求 e(i)、l(i)活动的最早、晚开始时间
   • e(i) = ve(j)活动的最早发生时间 = 对应顶点事件的最晚发生时间
   • l(i) = vl(k) - Wj,k对应顶点事件最迟发生时间减去活动的持续时间。
     • 如活动 a1 的最迟发生时间就是 V2 的六分钟减去 a1 持续的时间 6 分钟 = 0。也就是说活动 a1 现在立马就得开始。
3. 计算 l(i) - e(i)
   • 差值时间为 0 的活动是关键活动。
   • 由若干个关键活动所组成的路径就是关键路径

• 所以关键路径就是 a1 a4 a7 a8 a10 a11