后量子 KEM 方案:Newhope
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
参考文献
- Lyubashevsky V, Peikert C, Regev O. On ideal lattices and learning with errors over rings[J]. Journal of the ACM (JACM), 2013, 60(6): 1-35.
- Lyubashevsky V, Peikert C, Regev O. A toolkit for ring-LWE cryptography[C]//Advances in Cryptology–EUROCRYPT 2013: 32nd Annual International Conference on the Theory and Applications of Cryptographic Techniques, Athens, Greece, May 26-30, 2013. Proceedings 32. Springer Berlin Heidelberg, 2013: 35-54.
- Peikert C. Lattice cryptography for the internet[C]//Post-Quantum Cryptography: 6th International Workshop, PQCrypto 2014, Waterloo, ON, Canada, October 1-3, 2014. Proceedings 6. Springer International Publishing, 2014: 197-219.
- Alkim E, Ducas L, Pöppelmann T, et al. Post-quantum key exchange-A New Hope[C]//USENIX security symposium. 2016, 2016.
- Alkim E, Ducas L, Pöppelmann T, et al. NewHope without reconciliation[J]. Cryptology ePrint Archive, 2016.
- Alkim E, Ducas L, Pöppelmann T, et al. Post-quantum key exchange-A New Hope[C]//USENIX security symposium. 2016, 2016.
文章目录
Peikert’ KEM
基于 RLWE 的公钥密码基本上都遵从 LPR10 的类 ElGamal 框架。不同之处在于参数的选取以及各种纠错算法、压缩算法等等。
Peikert 使用 reconciliation和解 来实现密钥封装key encapsulation mechanism, KEM。
- 和解机制两方对一个带噪环元素上达成近似的共识它可以降低载荷大小
- 密钥封装发送方直接把对称密钥加密后发送给接收方这与 Diffie-Hellman 密钥交换协议不同KEM 只用到了发送者的随机性
密文空间是 C C C密钥空间是 K K K 的密钥封装方案是一组算法
- S e t u p ( ) Setup() Setup()输出公开参数 p p pp pp
- G e n ( p p ) Gen(pp) Gen(pp)输出公钥 p k pk pk 和私钥 s k sk sk
- E n c a p s ( p p , p k ) Encaps(pp,pk) Encaps(pp,pk)输出密文 c ∈ C c \in C c∈C 和密钥 k ∈ K k \in K k∈K
- D e c a p s ( s k , c ) Decaps(sk,c) Decaps(sk,c)输出一个 k ∈ K ∪ { ⊥ } k \in K \cup \{\perp\} k∈K∪{⊥}
Reconciliation
最开始和解机制由 Ding 提出但是这个方案是有偏斜的。Peikert 通过 “随机加倍” 的方式解决了偏斜问题。
限制
p
∣
q
p|q
p∣q定义
⌊
⋅
⌉
p
:
Z
q
→
Z
p
\lfloor \cdot \rceil_p: Z_q \to Z_p
⌊⋅⌉p:Zq→Zp 为
⌊
x
⌉
p
=
⌊
p
/
q
⋅
x
⌉
(
m
o
d
p
)
\lfloor x \rceil_p = \lfloor p/q \cdot x \rceil \pmod p
⌊x⌉p=⌊p/q⋅x⌉(modp)
将
Z
q
Z_q
Zq 上的元素圆整到
Z
p
Z_p
Zp 上。每个
Z
p
Z_p
Zp 上的点对应以它为中心的
q
/
p
q/p
q/p 长小区间的
Z
q
Z_q
Zq 上的点。
类似地定义
⌊
⋅
⌋
p
:
Z
q
→
Z
p
\lfloor \cdot \rfloor_p: Z_q \to Z_p
⌊⋅⌋p:Zq→Zp 为
⌊
x
⌋
p
=
⌊
p
/
q
⋅
x
⌋
(
m
o
d
p
)
\lfloor x \rfloor_p = \lfloor p/q \cdot x \rfloor \pmod p
⌊x⌋p=⌊p/q⋅x⌋(modp)
将
Z
q
Z_q
Zq 上的元素下取整整到
Z
p
Z_p
Zp 上。每个
Z
p
Z_p
Zp 上的点对应以它为左边界的
q
/
p
q/p
q/p 长小区间的
Z
q
Z_q
Zq 上的点。
Even Modulus
设置
p
=
2
p=2
p=2并且
q
q
q 是偶数。定义不交的区间
I
0
:
=
{
0
,
1
,
⋯
,
⌊
q
/
4
⌉
−
1
}
I
1
:
=
{
−
⌊
q
/
4
⌋
,
⋯
,
−
2
,
−
1
}
\begin{aligned} I_0 &:= \{0,1,\cdots,\lfloor q/4 \rceil -1\}\\ I_1 &:= \{-\lfloor q/4 \rfloor,\cdots,-2,-1\}\\ \end{aligned}
I0I1:={0,1,⋯,⌊q/4⌉−1}:={−⌊q/4⌋,⋯,−2,−1}
各自包含
Z
q
Z_q
Zq 上的
⌊
q
/
4
⌉
\lfloor q/4 \rceil
⌊q/4⌉ 和
⌊
q
/
4
⌋
\lfloor q/4 \rfloor
⌊q/4⌋ 个元素。
交叉圆整cross-rounding
⟨
⋅
⟩
2
:
Z
q
→
Z
2
\langle \cdot \rangle_2: Z_q \to Z_2
⟨⋅⟩2:Zq→Z2
⟨
v
⟩
2
:
=
⌊
4
/
q
⋅
v
⌋
(
m
o
d
2
)
\langle v \rangle_2 := \lfloor 4/q \cdot v \rfloor \pmod 2
⟨v⟩2:=⌊4/q⋅v⌋(mod2)
可以看出
⟨
v
⟩
2
=
b
∈
{
0
,
1
}
\langle v \rangle_2 = b \in \{0,1\}
⟨v⟩2=b∈{0,1}其中
v
∈
I
b
∪
(
q
2
+
I
b
)
v \in I_b \cup (\dfrac{q}{2}+I_b)
v∈Ib∪(2q+Ib)
可以这么理解将 Z q Z_q Zq 组织成一个一维环面最右端是 0 0 0最左端是 q / 2 q/2 q/2那么 I 0 I_0 I0 就是右上弧 I 1 I_1 I1 就是右下弧而 q 2 + I 0 \dfrac{q}{2}+I_0 2q+I0 是左下弧 q 2 + I 1 \dfrac{q}{2}+I_1 2q+I1 是左上弧。于是有
- 对于 ⌊ v ⌉ 2 \lfloor v \rceil_2 ⌊v⌉2 运算 I 0 I_0 I0 与 I 1 I_1 I1 上的元素被映射到 0 0 0而 q 2 + I 0 \dfrac{q}{2}+I_0 2q+I0 与 q 2 + I 1 \dfrac{q}{2}+I_1 2q+I1 上的元素被映射到 1 1 1
- 对于 ⟨ v ⟩ 2 \langle v \rangle_2 ⟨v⟩2 运算 I 0 I_0 I0 与 q 2 + I 0 \dfrac{q}{2}+I_0 2q+I0 上的元素被映射到 0 0 0而 I 1 I_1 I1 与 q 2 + I 1 \dfrac{q}{2}+I_1 2q+I1 上的元素被映射到 1 1 1
- 虽然由于圆整和下取整可能存在偏斜bias但是 ⟨ v ⟩ 2 \langle v \rangle_2 ⟨v⟩2 完美隐藏了 ⌊ v ⌉ 2 \lfloor v \rceil_2 ⌊v⌉2 的信息
如果 v , w ∈ Z q v,w \in Z_q v,w∈Zq 是足够接近的元素那么给定 w = v + e w=v+e w=v+e 与reconciliation information ⟨ v ⟩ 2 \langle v \rangle_2 ⟨v⟩2可以恢复出 ⌊ v ⌉ 2 \lfloor v \rceil_2 ⌊v⌉2
定义集合
E
:
=
[
−
q
8
,
q
8
)
∩
Z
E := \left[-\dfrac{q}{8},\dfrac{q}{8}\right) \cap \mathbb Z
E:=[−8q,8q)∩Z定义 reconciliation function
r
e
c
:
Z
q
×
Z
2
→
Z
2
rec: Z_q \times Z_2 \to Z_2
rec:Zq×Z2→Z2
r
e
c
(
w
,
b
)
:
=
{
0
,
w
∈
I
b
+
E
(
m
o
d
q
)
1
,
o
t
h
e
r
w
i
s
e
rec(w,b) := \left\{\begin{aligned} 0, && w \in I_b+E \pmod q\\ 1, && otherwise \end{aligned}\right.
rec(w,b):={0,1,w∈Ib+E(modq)otherwise
那么
r
e
c
(
w
,
⟨
v
⟩
2
)
=
⌊
v
⌉
2
rec(w,\langle v \rangle_2) = \lfloor v \rceil_2
rec(w,⟨v⟩2)=⌊v⌉2如图所示
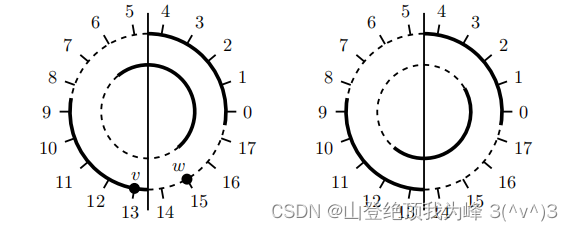
一维环面 Z q Z_q Zq 上 I 0 + E I_0+E I0+E 是右上的二分之一弧 I 1 + E I_1+E I1+E 是右下的二分之一弧。假设 v v v 的交叉圆整是 b b b由于 w = v + e w=v+e w=v+e 十分靠近 v v v如果 w ∈ I b + E w \in I_b+E w∈Ib+E那么说明 v v v 位于右边 b = 0 b=0 b=0在右上弧 b = 1 b=1 b=1在右下弧因此输出 ⌊ v ⌉ 2 = 0 \lfloor v \rceil_2 = 0 ⌊v⌉2=0否则 v v v 位于环面的左边输出 ⌊ v ⌉ 2 = 1 \lfloor v \rceil_2 = 1 ⌊v⌉2=1。
Odd Modulus
设置 p = 2 p=2 p=2并且 q q q 是奇数。此时由于不能平分 Z q Z_q Zq因此 ⌊ v ⌉ 2 = 0 / 1 \lfloor v \rceil_2 = 0/1 ⌊v⌉2=0/1 的比特将会出现偏斜。Peikert 使用随机加倍的方法消除了这个倾斜。
随机化函数
d
b
l
:
Z
q
→
Z
2
q
dbl: Z_q \to Z_{2q}
dbl:Zq→Z2q 定义为
v
ˉ
:
=
2
v
−
e
ˉ
(
m
o
d
2
q
)
\bar v := 2v - \bar e \pmod{2q}
vˉ:=2v−eˉ(mod2q)
其中 e ˉ ∈ { − 1 , 0 , 1 } \bar e \in \{-1,0,1\} eˉ∈{−1,0,1} 是模二均匀取 0 0 0 的概率为 0.5 0.5 0.5取 ± 1 \pm 1 ±1 的概率各为 0.25 0.25 0.25中心化的亚高斯分布的随机数。
由于解决了偏斜问题因此 ⟨ v ˉ ⟩ 2 \langle \bar v \rangle_2 ⟨vˉ⟩2 完美隐藏了 ⌊ v ˉ ⌉ 2 \lfloor \bar v \rceil_2 ⌊vˉ⌉2 的信息。
如果 w , v ∈ Z q w,v \in Z_q w,v∈Zq 十分接近那么 2 w , d b l ( v ) ∈ Z 2 q 2w,dbl(v) \in Z_{2q} 2w,dbl(v)∈Z2q 也十分接近从而使用 Z 2 q Z_{2q} Z2q偶数模上的 r e c ( ⋅ ) rec(\cdot) rec(⋅) 可以达成 ⌊ v ˉ ⌉ 2 = 0 / 1 \lfloor \bar v \rceil_2 = 0/1 ⌊vˉ⌉2=0/1 共识。注意 I 0 , I 1 , E I_0,I_1,E I0,I1,E 的取值范围。
Peikert’s KEM
IND-CPA
在 LPR13 中将 LPR10二的幂次分圆多项式环上 的 RLWE 扩展到了任意的环并提出了一套快速计算的工具包括 powerful basis用于张量分解, CRT basis用于类 FFT 乘法, decoding basis用于 BDD 解码。看不懂分数理想、对偶空间。
给定环
R
q
:
=
Z
q
[
x
]
/
(
m
(
x
)
)
R_q := Z_q[x]/(m(x))
Rq:=Zq[x]/(m(x)) 的一组 decoding basis
D
=
{
d
j
}
D = \{d_j\}
D={dj}那么环元素可以坐标表示为
v
=
∑
j
v
j
⋅
d
j
∈
R
q
v = \sum_j v_j \cdot d_j \in R_q
v=j∑vj⋅dj∈Rq
从整数环
Z
\mathbb Z
Z 扩展到分圆环
R
:
=
Z
[
ζ
m
]
⊂
K
:
=
Q
[
ζ
m
]
R:= \mathbb Z[\zeta_m] \subset K:=\mathbb Q[\zeta_m]
R:=Z[ζm]⊂K:=Q[ζm]定义
⌊
v
⌉
2
:
R
q
→
R
2
\lfloor v \rceil_2:R_q \to R_2
⌊v⌉2:Rq→R2
⌊
v
⌉
2
:
=
∑
j
⌊
v
j
⌉
2
⋅
d
j
\lfloor v \rceil_2 := \sum_j \lfloor v_j \rceil_2 \cdot d_j
⌊v⌉2:=j∑⌊vj⌉2⋅dj
类似的定义
⟨
v
⟩
2
:
R
q
→
R
2
\langle v \rangle_2:R_q \to R_2
⟨v⟩2:Rq→R2
⟨
v
⟩
2
:
=
∑
j
⟨
v
j
⟩
2
⋅
d
j
\langle v \rangle_2 := \sum_j \langle v_j \rangle_2 \cdot d_j
⟨v⟩2:=j∑⟨vj⟩2⋅dj
对于偶数模定义
r
e
c
:
R
q
×
R
2
→
R
2
rec:R_q \times R_2 \to R_2
rec:Rq×R2→R2
r
e
c
(
w
,
b
)
:
=
∑
j
r
e
c
(
w
j
,
b
j
)
⋅
d
j
rec(w,b) := \sum_j rec(w_j,b_j) \cdot d_j
rec(w,b):=j∑rec(wj,bj)⋅dj
对于奇数模定义
d
b
l
:
R
q
→
R
2
q
dbl: R_q \to R_{2q}
dbl:Rq→R2q
d
b
l
(
v
)
:
=
∑
j
d
b
l
(
v
j
)
⋅
d
j
dbl(v) := \sum_j dbl(v_j) \cdot d_j
dbl(v):=j∑dbl(vj)⋅dj
Peikert’s KEM 使用的还是 LPR10 定义的简化版 RLWE 问题。算法如下

在两样本的 R − D L W E q , χ R-DLWE_{q,\chi} R−DLWEq,χ 假设下上述的 KEM 算法是 IND-CPA 安全的。
IND-CCA
可以使用 Fujisaki-Okamoto transformation 来获得 IND-CCA 安全的 KEM。
Peikert 也尝试了其他的转换方案但都有各种各样的问题。后续的密钥封装方案Newhope, LAC也都是先构造 IND-CPA 的 KEM然后再用 FO 转换获得 IND-CCA 的 KEM。
密钥封装方案 KEM 和公钥加密方案 PKE 是等价的
- 使用 One-padding 方式可以从 KEM 自然的转化为 PKE 方案。
- 随机生成 key 然后使用 PKE 加密发送这就是一个 KEM 方案。
Newhope - reconciliation
Newhope 进入了 NIST 后量子征集的第二轮但没有进入第三轮。它使用了十分类似 Peikert’s KEM 的方案。
参数选取
Newhope 使用了二的幂次分圆环 R q = Z q [ X ] / ( X n + 1 ) R_q = \mathbb Z_q[X]/(X^n+1) Rq=Zq[X]/(Xn+1)其中 n = 1024 n=1024 n=1024 q = 12289 q=12289 q=12289 是满足 2 n ∣ q − 1 2n \mid q-1 2n∣q−1 的最小素数为了使用 NTT 加速。
另外由于高精度的离散高斯分布会消耗大量的熵实际实现时效率不高。因此Newhope 采用了中心化二项分布centered binomial distribution
Ψ
k
\Psi_k
Ψk计算方法是
∑
i
=
1
k
b
i
−
b
i
′
\sum_{i=1}^k b_i - b_i'
i=1∑kbi−bi′
其中 b i , b i ′ ∈ { 0 , 1 } b_i,b_i' \in \{0,1\} bi,bi′∈{0,1} 是独立的均匀随机比特。Newhope 选取了 k = 16 k=16 k=16标准差为 k / 2 = 2 2 \sqrt{k/2} = 2\sqrt 2 k/2=22
四维格上的和解
为了降低解密错误率Newhope 选择了密钥空间 { 0 , 1 } 256 \{0,1\}^{256} {0,1}256将每 1 1 1 比特编码到 4 4 4 个系数上。
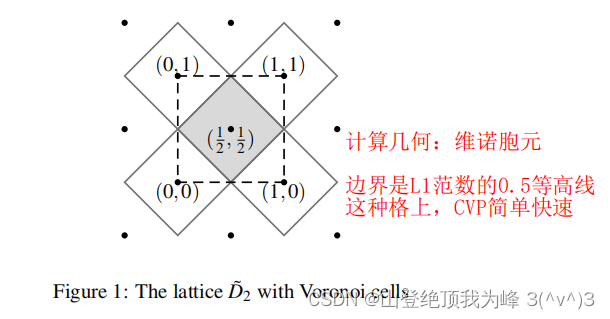
方便理解我们首先考虑二维格 D ~ 2 \tilde D_2 D~2它的基底为 { ( 0 , 1 ) , ( 0.5 , 0.5 ) } \{(0,1),(0.5,0.5)\} {(0,1),(0.5,0.5)}如图所示
将每个比特对应的
2
2
2 个整系数
Z
q
2
Z_q^2
Zq2 平凡地映射到
[
0
,
1
)
2
=
R
2
/
Z
2
[0,1)^2 = \mathbb R^2/\mathbb Z^2
[0,1)2=R2/Z2 上向量
x
x
x在虚线围成的正方形中灰色的部分Voronoi cell被解码为
0
0
0白色的部分被解码为
1
1
1面积各占
1
2
\dfrac{1}{2}
21两个区域的边界是到点
(
0.5
,
0.5
)
(0.5,0.5)
(0.5,0.5) 的 L1 范数的
0.5
0.5
0.5 等高线。 因此这个 BDD 解码过程是特别简单高效的
但是如果发送者向量 x s x_s xs 和接收者向量 x c x_c xc 恰好在边界附近即使 x c , x s x_c,x_s xc,xs 很接近依然可能会出现和解失败的情况。Newhope 使用 x s x_s xs 与它所在的 Voronoi cell 中心点的向量差 r r r 作为 reconciliation vector辅助 r e c ( x , r ) rec(x,r) rec(x,r) 的计算接收者获取 r r r 后计算 x s + r x_s+r xs+r 向对应的中心倾斜以跨越边界。
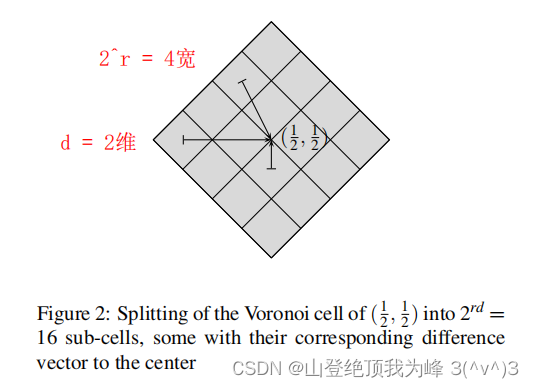
另外为了压缩载荷Newhope 对 Voronoi cell 进行了离散化也就是把每个坐标分量从 Z q Z_q Zq 圆整到 Z 2 r Z_{2^r} Z2r 上r-bit discretization保留了 MSB 信息。为了消除奇数模 q q q 导致的 small bias以 1 2 \dfrac{1}{2} 21的概率添加 ( 1 2 q , 1 2 q ) (\dfrac{1}{2q},\dfrac{1}{2q}) (2q1,2q1) 到 x x x 上这叫做 Blurring the edges。
Newhope 使用的是
d
=
4
d=4
d=4 维格
D
~
4
\tilde D_4
D~4基底
{
u
1
,
u
2
,
u
3
,
g
=
(
0
,
5
,
0.5
,
0.5
,
0.5
)
}
\{u_1,u_2,u_3,g=(0,5,0.5,0.5,0.5)\}
{u1,u2,u3,g=(0,5,0.5,0.5,0.5)}其中
u
i
u_i
ui 是
Z
4
\mathbb Z^4
Z4 的单位正交基。此时根据上述
D
~
2
\tilde D_2
D~2 的和解思路
H
e
l
p
R
e
c
(
x
;
b
)
:
=
C
V
P
D
~
4
(
2
r
q
(
x
+
b
g
)
)
(
m
o
d
2
r
)
∈
{
0
,
1
,
2
,
3
}
4
R
e
c
(
x
;
r
)
:
=
D
e
c
o
d
e
(
1
q
x
−
1
2
r
B
r
)
∈
{
0
,
1
}
\begin{aligned} HelpRec(x;b) &:= CVP_{\tilde D_4}\left( \dfrac{2^r}{q}(x+bg) \right) \pmod{2^r} \in \{0,1,2,3\}^4\\ Rec(x;r) &:= Decode\left(\dfrac{1}{q}x - \dfrac{1}{2^r}Br\right) \in \{0,1\} \end{aligned}
HelpRec(x;b)Rec(x;r):=CVPD~4(q2r(x+bg))(mod2r)∈{0,1,2,3}4:=Decode(q1x−2r1Br)∈{0,1}
其中的 C V P CVP CVP 和 D e c o d e Decode Decode 算法如下

Newhope 使用了 2 2 2 比特位离散化因此 key 的每个比特需要 r ⋅ d = 2 × 4 = 8 r \cdot d = 2 \times 4 = 8 r⋅d=2×4=8 比特的 reconciliation information。
KEM 方案
Newhope 使用了 NTT 算法、Montgomery reduction 算法、Short Barrett reduction 算法加速环上的运算。另外使用 SHA-3 标准里的 SHAKE128、SHAKE256 来实例化 PRG、Hash、XOF 等功能。
IND-CPA 安全的 KEM 方案如下
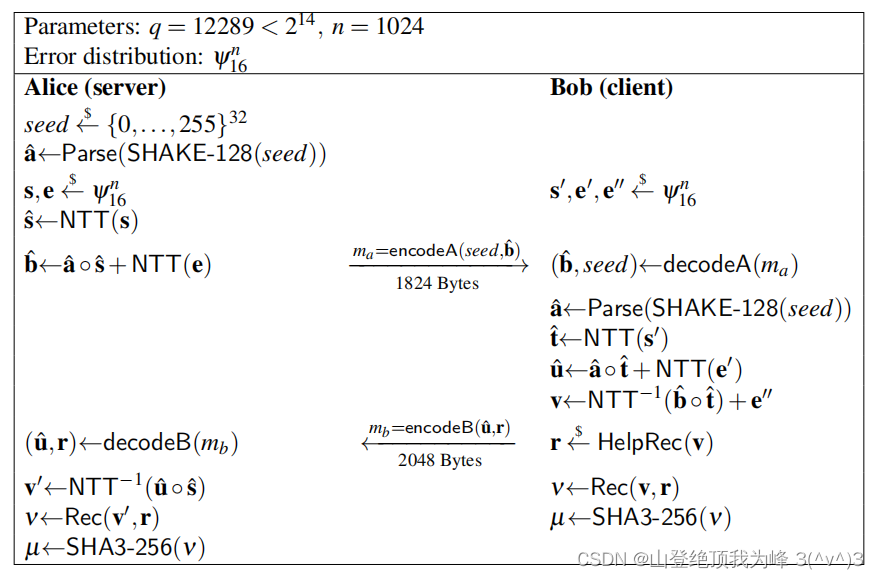
类似 Peikert’s KEMNewhope 也使用 FO 转换来获得 IND-CCA 安全的 KEM。
Newhope - Simple
基于和解机制的 KEM 的优点是载荷很小。不过上边描述的 Newhope 较为复杂不容易理解和实现。后续Newhope 给出了另一种方案不再使用和解机制而是通过 “舍入”或者说 “模切换” 直接丢弃低位比特。
方案描述
编码函数就是 Regev 的 MSB 编码方式为
k
=
E
n
c
o
d
e
(
v
∈
{
0
,
1
}
n
)
:
=
∑
i
=
0
n
−
1
k
i
⋅
⌊
q
2
⌋
⋅
X
i
k = Encode(v \in \{0,1\}^n) := \sum_{i=0}^{n-1} k_i \cdot \left\lfloor \dfrac{q}{2} \right\rfloor \cdot X^i
k=Encode(v∈{0,1}n):=i=0∑n−1ki⋅⌊2q⌋⋅Xi
降低载荷规模的思路为由于噪声集中在低位比特把它们简单丢弃视作“模切换”。在通信时直接丢弃 k k k 的各项系数的低位比特得到 k ′ k' k′ 发送给对方。
解码函数提取 MSB为
μ
=
E
x
t
r
a
c
t
(
k
′
)
:
=
{
μ
i
=
1
,
v
i
∈
[
−
⌊
q
2
⌋
,
⌊
q
2
⌋
)
μ
i
=
0
,
o
t
h
e
r
w
i
s
e
}
,
∀
i
=
0
,
⋯
,
n
−
1
\mu = Extract(k') := \left\{\begin{aligned} \mu_i = 1, && v_i \in \left[-\left\lfloor \dfrac{q}{2} \right\rfloor,\left\lfloor \dfrac{q}{2} \right\rfloor\right)\\ \mu_i = 0, && otherwise \end{aligned}\right\}, \forall i=0,\cdots,n-1
μ=Extract(k′):=⎩
⎨
⎧μi=1,μi=0,vi∈[−⌊2q⌋,⌊2q⌋)otherwise⎭
⎬
⎫,∀i=0,⋯,n−1
Encryption-based KEM 与 Reconciliation-based KEM 的对比如下

Newhope - Simple 比前述的基于和解的 Newhope仅仅只有很小的载荷损失上涨了 6.25 % 6.25\% 6.25%并拥有相同的安全性。
代码描述
为了降低解密错误率Newhope-Simple 使用了 D2/D4 重复码

密文压缩算法就是丢弃低位比特

使用 NTT 等加速算法最终的 Newhope - Simple 算法如下


