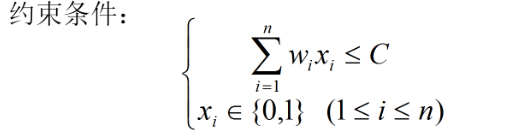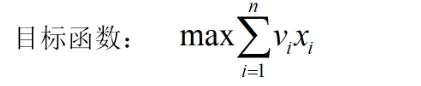算法第十四期——动态规划(DP)初入门
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
目录
DP初步:状态转移与递推
最少硬币问题
有多个不同面值的硬币任意面值)数量不限输入金额s输出最少硬币组合。
例硬币面值1、2、5。支付13元要求硬币数量最少
例硬币面值1、2、4、5、6。支付9元要求硬币数量最少
回顾用贪心求解硬币问题但只能得到局部最优解不能得到全局最优。
硬币问题的正解是动态规划
DP基础
type = [15102550] # 5种面值
定义数组Min[ ]记录最少硬币数量:
对输入的某个金额iMin[i]是最少的硬币数量。把Min[ ]叫做“状态”
第一步:只考虑1元面值的硬币

把Min[ ]的变化叫做“状态转移”
- i=1元时等价于: i= i-1=0元需要的硬币数量加上1个1元硬币。
继续所有金额仍然都只用1元硬币
- i=2元时等价于: i= i-1 =1元需要的硬币数量加上1个1元硬币。
- i=3元时...
- i=4元时...
在1元硬币的计算结果基础上再考虑加上5元硬币的情况。从i=5开始就行了: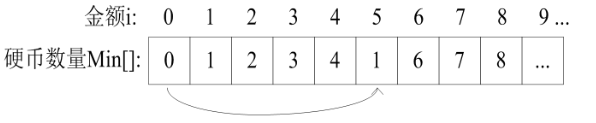
- i=5元时等价于:
(1) i = i-5 =0元需要的硬币数量加上1个5元硬币。Min[5]=1。
(2原来只使用1元硬币Min[5]=5。
取(1) (2)的最小值所以Min[5]=1。

- i=6元时等价于:
(1) i = i - 5= 1元需要的硬币数量加上1个5元硬币。Min[6] = 2
(2原来只使用1元硬币Min[6] = 6
取1(2的最小值所以Min[6] = 2
- i=7元时…
- i=8元时…
用1元和5元硬币结果:
递推关系: Min[i]= min(Min[i], Min[i - 5]+ 1 ) 状态转移方程
【代码】
def solve(s):
Min = [int(1e12)]*(s+1) # 初始化为无穷大
Min[0] = 0
for j in range(cnt) : # 5种硬币
for i in range(type[j], s+1):
Min[i] = min(Min[i],Min[i - type[j]] +1) # 递推关系
print (Min[s])
cnt = 5 # 5种硬币
type = [1,5,10,25,50] # 5种面值
s = int(input())
solve(s)递推关系min(Min[ i ],Min[ i - type[ j ] ] +1)
习惯上把状态命名为dp[ ] 所以应该把Min[ ]改成dp[ ]。
DP的两个特征
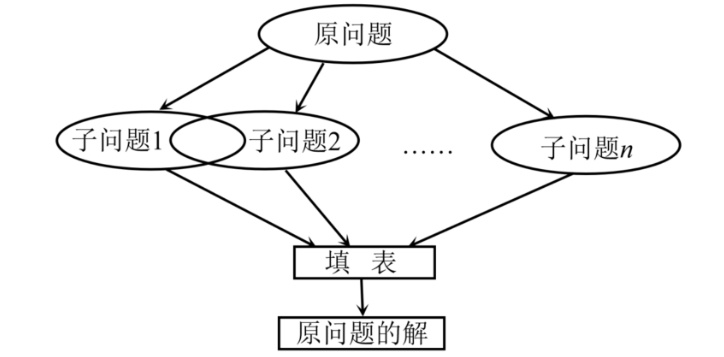
(1重叠子问题。子问题是原大问题的小版本计算步骤完全一样;计算大问题的时候需要多次重复计算小问题。
一个子问题的多次计算耗费了大量时间。用DP处理重叠子问题每个子问题只需要计算一次从而避免了重复计算这就是DP效率高的原因。
(2最优子结构。首先大问题的最优解包含小问题的最优解其次可以通过小问题的最优解推导出大问题的最优解例如100块钱的最小硬币数包括90块钱的最小硬币数100块钱的最小硬币数是由90块钱的最小硬币数推导过来的。
DP:记忆化
- 如果各个子问题不是独立的如果能够保存已经解决的子问题的答案在需要的时候再找出已求得的答案可以避免大量的重复计算
- 基本思路:用一个表记录所有已解决的子问题的答案不管该问题以后是否被用到只要它被计算过就将其结果填入表中。
图解DP求解过程
最经典的DP问题0/1背包
- 给定n种物品和一个背包物品i的重量是
其价值为
背包的容量为C。
- 背包问题选择装入背包的物品使得装入背包中物品的总价值最大。
- 如果在选择装入背包的物品时对每种物品i只有两种选择:装入背包或不装入背包称为0/1背包问题。
设
表示 物品i 装入背包的情况,
=0表示 物品i 没有被装入背包
=1表示 物品i 被装入背包
首先讲一下暴力法求解遍历所有情况n个物品的话是种情况因为每个物品有放入和不放入两种情况。 如果n>=1000的话可以用暴力法解决如果n>1000那只能使用动态规划来求解。
例有5个物品重量分别是{2,2,6,5,4}价值分别为{6,3,5,4,6}背包的容量为10。物品个数为n容量为C定义一个(n+1)×(C+1)的二维表dp[ ][ ]两个+1是因为0行和0列我们是不需要的
dp[i][j]表示把前 i 个物品装入容量为 j 的背包中获得的最大价值。
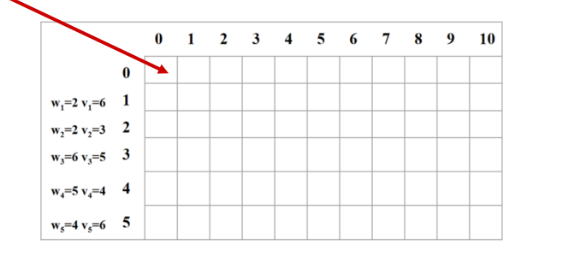
填表按只放第1个物品、只放前2个、只放前3个....一直到放完这样的顺序考虑。(从小问题扩展到大问题)
1、只装第1个物品。(表格横向是递增的背包容量)
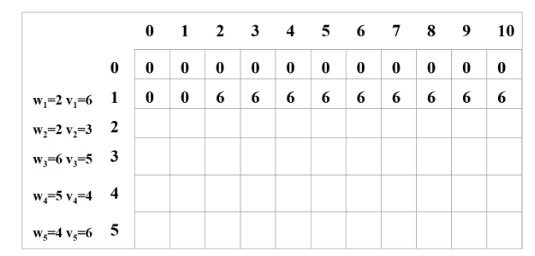
2、只装前2个物品。
如果第2个物品重量比背包容量大那么不能装第2个物品情况和只装第1个一样。

如果第2个物品重量小于等于背包容量那么:
(1如果把物品2装进去(重量是2)那么相当于只把1装到(容量-2)的背包中。

两个都装得下就把两个都装下去。

需要用到前面的结果即已经解决的子问题的答案。
(2如果不装2那么相当于只把1装到背包中。

两个都装得下但选择只把1装到背包中。
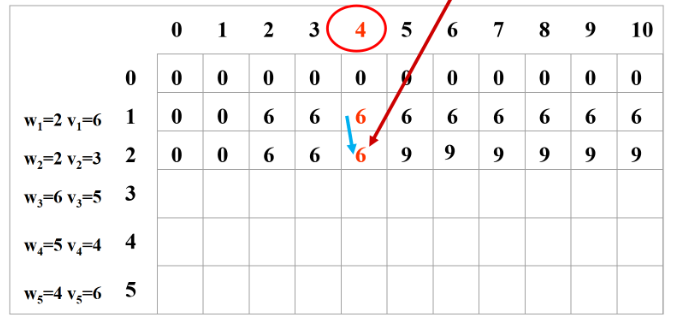 最后取(1和2的最大值。
最后取(1和2的最大值。
3、只装前3个物品。
如果第3个物品重量比背包大那么不能装第3个物品情况和只装第、2个一样。例如容量在1~5的时候情况和和只装第、2个一样。
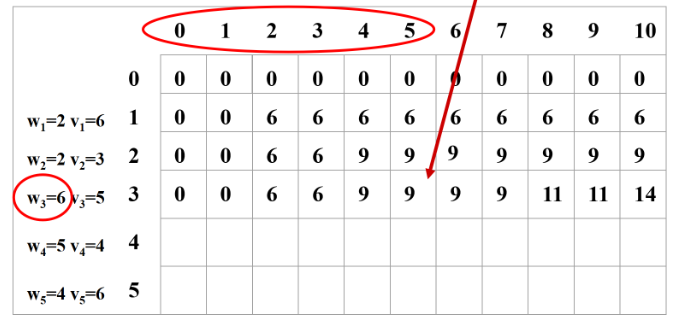
如果第3个物品重量小于等于背包容量那么:
(1装3重量是6那么相当于只把1、2装到(容量-6)的背包中。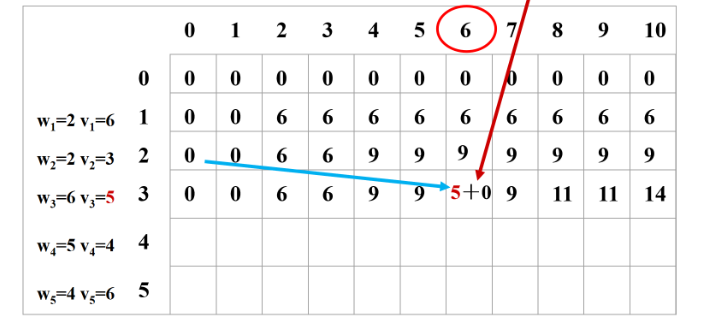

2不装3那么相当于只把1、2装到背包中。一取(1和(2的最大值。
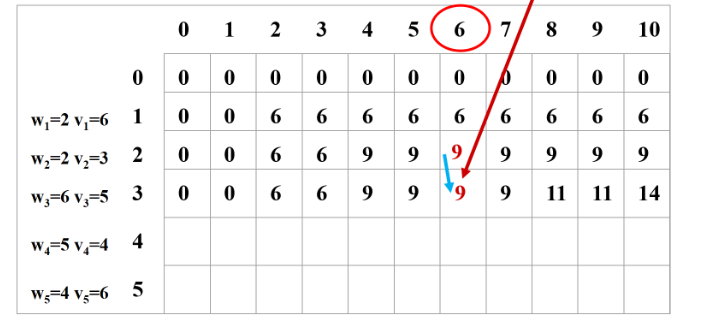
按这样的规律一行行填表直到结束。
装了那些物品看每 i 行同一容量如果价值和上一行相等则没有装物品 i 否则装了物品 i 。看最后一列15>14说明装了物品5否则价值不会变化。
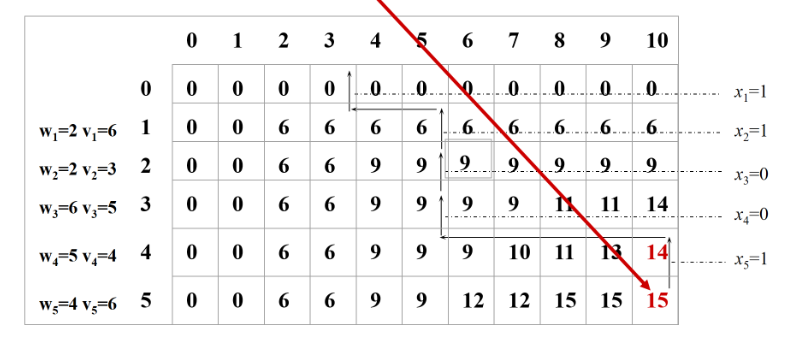 DP的复杂度O(n*c)n是物品数c是容量。
DP的复杂度O(n*c)n是物品数c是容量。
模板题小明的背包
题目描述
小明有一个容量为 C 的背包。
这天他去商场购物商场一共有 N 件物品第 i 件物品的体积为
价值为
。
小明想知道在购买的物品总体积不超过 C 的情况下所能获得的最大价值为多少请你帮他算算。
输入描述
输入第 1 行包含两个正整数 N,C表示商场物品的数量和小明的背包容量。
第 2∼N+1 行包含 2 个正整数c,w表示物品的体积和价值。
1≤N≤10^21≤C≤10^31≤
,
≤10^3。
输出描述
输出一行整数表示小明所能获得的最大价值。
输入输出样例
输入
5 20 1 6 2 5 3 8 5 15 3 3输出
37
DP状态设计
DP状态定义二维数组dp[ ][ ]大小为N×C。
dp[i][j]把前i个物品从第1个到第 i 个选择性装入容量为 j 的背包中获得的最大价值。
把每个dpli][j]看成一个背包:背包容量为j装1~i这些物品。最后得到的dp[N][C]就是问题的答案:把N个物品装进容量C的背包的最大价值。
DP状态转移方程重点
递推计算到dp[i][j]分2种情况:
(1第 i 个物品的体积比容量 j 还大不能装进容量 j 的背包。那么直接继承前 i-1 个物品装进容量j的背包的情况即可:dp[i][j] = dp[i-1][j]。
(2第i个物品的体积比容量j小能装进背包。又可以分为2种情况:装或者不装第i个。
- 装第i个。从前i-1个物品的情况下推广而来前i-1个物品是dp[i-1][j]。第i个物品装进背包后背包容量减少c[i]价值增加w[i]。有:dp[i][j] = dp[i-1][j-c[i]] + w[i]。其中dp[i-1][j-c[i]]用剩下的容量去装最大价值的物品
- 不装第i个。那么直接继承前 i-1 个物品装进容量j的背包的情况: dp[i][j] = dp[i-1][j]。
- 取1和2的最大值状态转移方程:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - c[i]] + w[i])
代码
def solve(n,C):
# 遍历dp矩阵填表
for i in range(1, n+1):
for j in range (0,C+1):
if c[i]>j: dp[i][j] = dp[i-1][j]
else: dp[i][j] = max(dp[i-1][j], dp[i-1][j-c[i]]+w[i])
return dp[n][C]
N=3011
dp = [[0]*N for j in range(N)] # 初始化dp
# 或者这样写: dp = [[0 for i in range (N)] for j in range(N)]
w = [0]*N
c = [0]*N
n,C = map(int,input ().split())
for i in range(1, n+1):
c[i], w[i] = map(int,input ().split())
print(solve(n,C))空间优化:滚动数组
把dp[ ][ ]优化成一维的dp[ ]以节省空间。
dp[i][ ]是从上面一行dp[i-1]算出来的第i行只跟第i-1行有关系跟更前面的行没有关系:
dp[i][j]= max(dp[i - 1][j], dp[i - 1][j - c[i]]+w[i])
优化:只需要两行dp[0][ ]、dp[1][ ]用新的一行覆盖原来的一行交替滚动。
经过优化空间复杂度从O(N×C)减少为O(C)。
(1交替滚动两行
定义dp[ ][i]:用dp[0][ ]和dp[1][ ]交替滚动。
dp[now][j] = max(dp[old][j], dp[old][j-c[i]]+w[i])
优点:逻辑清晰、编码不易出错建议初学者采用这个方法。

例如上图的两行第一行i-1被第二行的i用完就用i+1覆盖第一行的i-1然后第二行的i被i+1用完就用用i+2覆盖第二行的i以此类推哪一行用完就用新的一行覆盖。
做法now始终指向正在计算的最新的一行old指向已计算过的旧的一行。对照原递推代码now相当于iold相当于i-1。
def solve(n, C):
now = 0;old = 1 # 初始化两行
for i in range(1, n+1):
old, now = now, old # 交换
for j in range (0,C+1):
if c[i] >j: dp[now][j] = dp[old][j] # dp[i][j] = dp[i-1][j]
else: dp[now][j] = max(dp[old][j], dp[old][j-c[i]]+w[i]) # dp[i][j] = max(dp[i-1][j], dp[i-1][j-c[i]]+w[i])
return dp[now][C]
N = 3011
dp = [[0 for i in range(N)] for j in range(2)] #注意先后
w = [0]*N
c = [0]*N
n,C = map(int,input().split())
for i in range(1, n+1):
c[i], w[i] = map(int,input().split())
print(solve(n,C))(2自我滚动一行
继续精简用一个一维的dp[ ]就够了自己滚动自己。
原式中dp[i][j] = max(dp[i-1][j], dp[i-1][j-c[i]]+w[i])的右边两个dp[i-1]是同一个行所以只需要一行用之前计算的结果赋值给现在的自己即可类似于a=a+1。
自我滚动dp[j] = max(dp[j], dp[j-c[i]]+w[i])
def solve(n,C):
for i in range(1, n+1):
for j in range (C,c[i]-1,-1): # 倒过来
dp[j] = max(dp[j], dp[j-c[i]]+w[i])
return dp[C]
N = 3011
dp = [0]*N
w = [0]*N
c = [0]*N
n,C = map(int,input ().split())
for i in range(1,n+1):
c[i], w[i] = map(int,input().split())
print(solve(n,C))为什么容量C是从大到小循环呢
j从小往大循环是错误的
 例如i = 2时左图的dp[5]经计算得到dp[5] = 9把dp[5]更新为9。
例如i = 2时左图的dp[5]经计算得到dp[5] = 9把dp[5]更新为9。
右图中继续往后计算当计算dp[8]时得dp[8] = dp[5]’+3= 9+3 = 12这个答案是错的。
错误的产生是滚动数组重复使用同一个空间引起的。
j从大到小循环是对的

例如i = 2时首先计算最后的dp[9] = 9它不影响前面状态的计算。