Pytorch优化器全总结(三)牛顿法、BFGS、L-BFGS 含代码
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
目录
优化器系列文章列表
Pytorch优化器全总结一SGD、ASGD、Rprop、Adagrad
Pytorch优化器全总结二Adadelta、RMSprop、Adam、Adamax、AdamW、NAdam、SparseAdam
Pytorch优化器全总结三牛顿法、BFGS、L-BFGS 含代码
写在前面
这篇文章是优化器系列的第三篇主要介绍牛顿法、BFGS和L-BFGS其中BFGS是拟牛顿法的一种而L-BFGS是对BFGS的优化那么事情还要从牛顿法开始说起。
一、牛顿法
函数最优化算法方法不唯一其中耳熟能详的包括梯度下降法梯度下降法是一种基于迭代的一阶优化方法优点是计算简单牛顿法也是一种很重要的优化方法是基于迭代的二阶优化方法优点是迭代次数少收敛速度很快。下面我们简要介绍一下牛顿法。
1.看图理解牛顿法
最优化问题就是寻找能使函数最小化的x所以目标函数应当是一个凸函数起码是局部凸函数假如一个函数如下图
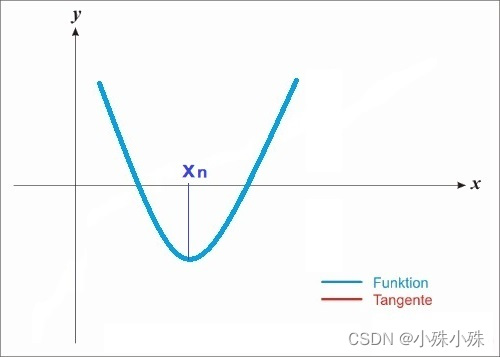
图1
他的一阶导数可能长下面这个样子
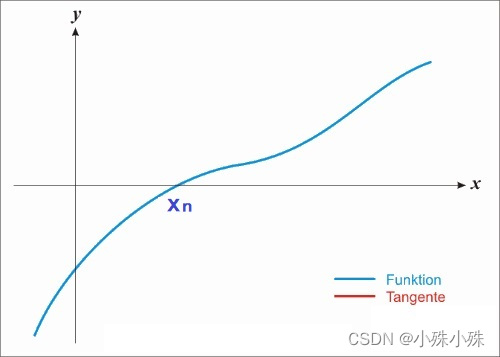
图2
很显然函数在处取得最小值同时这个点的导数等于0如果使用梯度下降经过多次迭代x的取值会慢慢接近
我们都能想象这个过程。
如果使用牛顿法x也会逼近不过速度会快很多示例图如下
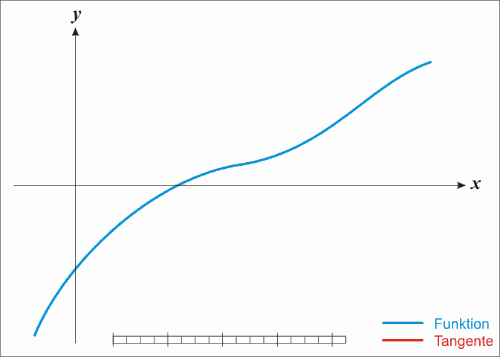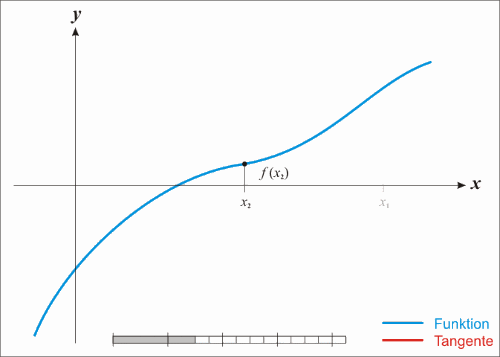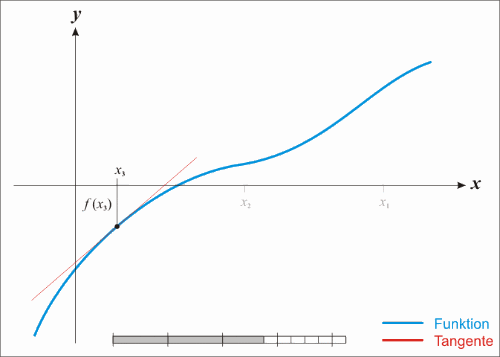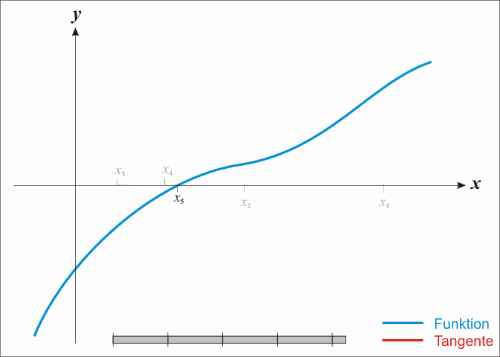
图3
这个过程可以这样描述
a.在X轴上随机一点,经过
做X轴的垂线,得到垂线与函数图像的交点
.
b.通过做函数的切线,得到切线与X轴的交点
.
c.迭代a/b两步当前后两次求的x相同或者两个值的差小于一个阈值的时候我们就认为找到了。
三个步骤的难点在于b如何快速的找到切线与X轴的交点下面有两种计算方式思想不同但结果是一样的。
2.公式推导-三角函数
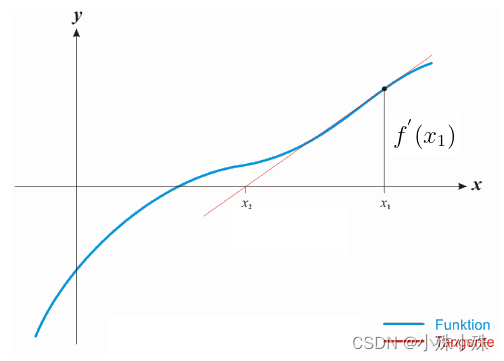
图4
如图4蓝色的线是函数的的导数
则曲线在
处的导数为
我们要求
根据三角函数有
1
得出
2
利用开始进行下一轮的迭代。迭代公式可以简化如下
3
3.公式推导-二阶泰勒展开
任意一点在附近的二阶泰勒展开公式为
4
对求导
5
令:
6
写成迭代形式
7
可以看到使用三角函数和二阶泰勒展开最终得到的结果是一样的。虽然牛顿法收敛速度很快但是当x的维度特别多的时候我们想求得是非常困难的而牛顿法又是一个迭代算法,所以这个困难我们还要面临无限多次导致了直接使用牛顿法最为优化算法很难实际落地。为了解决这个问题出现了拟牛顿法下面介绍一种拟牛顿法BFGS主要就是想办法一种方法代替二阶导数。
二、BFGS公式推导
函数 在
处的二阶泰勒展开式为
8
当x为向量的时候上式写成
9
令同时对
求导
10
接下来我们要想办法去掉我们使用
代替
是在迭代中一点点计算出来的而不使用二阶导数。
上式变为:
11
12
我们认为每次迭代与上次变化
形式如下
13
令
14
将式1314带入式子12
15
令
16
其中 均为
的向量带入15
17
18
已知 为实数
为向量。式18中参数
和
解的可能性有很多我们取特殊的情况假设
。带入16得
19
将 带入18得
20
21
令 则
22
令则
23
将式22和23带入19
24
将24带入13得到的迭代公式
24
当x为向量的时候式7写成
25
加上学习率得到BFGS的迭代公式
26
我们发现还需要求的逆这里可以引入sherman-morrism公式求解
的逆
27
我们用代替
得到最终的BFGS迭代公式和
的迭代公式
28
29
其中是本轮x与上一轮x的差
是本轮梯度与上一轮梯度的差。
三、L-BFGS
在BFGS算法中仍然有缺陷每次迭代计算需要前次迭代得到的的存储空间至少为N(N+1)/2N为特征维数对于高维的应用场景需要的存储空间将是非常巨大的。为了解决这个问题就有了L-BFGS算法。L-BFGS即Limited-memory BFGS。 L-BFGS的基本思想就是通过存储前m次迭代的少量数据来替代前一次的矩阵从而大大减少数据的存储空间。
令则式29可以表示为
30
若在初始时假定初始的矩阵则我们可以得到
31
32
假设当前迭代为n只保存最近的m次迭代信息按照上面的方式迭代m次可以得到如下的公式
由于这些变量都最终可以由s、y两个向量计算得到因此我们只需存储最后m次的s、y向量即可算出
加上对角阵
总共需要存储2*m+1个N维向量实际应用中m一般取4到7之间的值因此需要存储的数据远小于Hesse矩阵。
四、算法迭代过程
1. 选初始点最小梯度阈值
存储最近 m 次的选代数据
2.初始化
3.如果则返回最优解 x否则转入步骤4
4.计算本次选代的可行方向
5.计算步长用下面的式子进行线搜索
6.用下面的更新公式更新x
7.如果 n大于 m保留最近 m 次的向量对删除
8.计算并保存向量对
9.用 two-loop recursion算法求
10.设置转到步骤3
五、代码实现
1.torch.optim.LBFGS说明
该类实现 LBFGS优化方法。LBFGS是什么已经不用多说了。
Pytorch说明文档LBFGS — PyTorch 1.13 documentation
'''
lr (float): 学习率 (default: 1)
max_iter (int): 每个优化步骤的最大迭代次数就像图3那样迭代 (default: 20)
max_eval (int): 每次优化函数计算的最大数量使用了线搜索算法时每次迭代计数器可能增加不止1最好使用线搜索算法时再设置这个参数。计数器同时受max_iter 和max_eval约束先到哪个值直接跳出迭代。(default: max_iter * 1.25).
tolerance_grad (float): 一阶最优终止公差就是指yn (default: 1e-5).
tolerance_change (float): 函数值/参数变化的终止容差,就是指sn (default: 1e-9).
history_size (int): 更新历史记录大小 (default: 100).
line_search_fn (str): 使用线搜索算法只能是'strong_wolfe' 或者None (default: None).
'''
class torch.optim.LBFGS(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)2.使用LBFGS优化模型
我们用一个简单的全连接网络并使用LBFGS优化下面是代码和运行结果可以看到损失下降的速度还是很快的。
# coding=utf-8
#================================================================
#
# File name : optim_duibi.py
# Author : Faye
# Created date: 2022/8/26 17:30
# Description :
#
#================================================================
import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt
# 超参数
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
# 生成假数据
# torch.unsqueeze() 的作用是将一维变二维torch只能处理二维的数据
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1) # x data (tensor), shape(100, 1)
# 0.2 * torch.rand(x.size())增加噪点
y = x.pow(2) + 0.1 * torch.normal(torch.zeros(*x.size()))
# 定义数据库
dataset = Data.TensorDataset(x, y)
# 定义数据加载器
loader = Data.DataLoader(dataset=dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=0)
# 定义pytorch网络
class Net(torch.nn.Module):
def __init__(self, n_features, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_features, n_hidden)
self.predict = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
x = F.relu(self.hidden(x))
y = self.predict(x)
return y
# 定义不同的优化器网络
net_LBFGS = Net(1, 10, 1)
# 选择不同的优化方法
opt_LBFGS = torch.optim.LBFGS(net_LBFGS.parameters(), lr=LR, max_iter=20)
nets = [net_LBFGS]
optimizers = [opt_LBFGS]
# 选择损失函数
loss_func = torch.nn.MSELoss()
# 不同方法的loss
loss_LBFGS = []
# 保存所有loss
losses = [loss_LBFGS]
# 执行训练
for epoch in range(EPOCH):
for step, (batch_x, batch_y) in enumerate(loader):
var_x = Variable(batch_x)
var_y = Variable(batch_y)
for net, optimizer, loss_history in zip(nets, optimizers, losses):
if isinstance(optimizer, torch.optim.LBFGS):
def closure():
y_pred = net(var_x)
loss = loss_func(y_pred, var_y)
optimizer.zero_grad()
loss.backward()
return loss
loss = optimizer.step(closure)
else:
# 对x进行预测
prediction = net(var_x)
# 计算损失
loss = loss_func(prediction, var_y)
# 每次迭代清空上一次的梯度
optimizer.zero_grad()
# 反向传播
loss.backward()
# 更新梯度
optimizer.step()
# 保存loss记录
loss_history.append(loss.data)
# 画图
labels = ['LBFGS']
for i, loss_history in enumerate(losses):
plt.plot(loss_history, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()
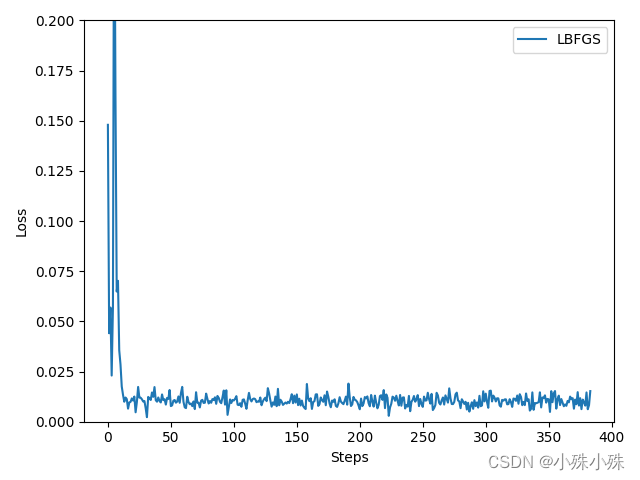
牛顿法、BFGS和L-BFGS就介绍到这里后面我将对比所有优化算法的性能收藏关注不迷路。
优化器系列文章列表
Pytorch优化器全总结一SGD、ASGD、Rprop、Adagrad
Pytorch优化器全总结二Adadelta、RMSprop、Adam、Adamax、AdamW、NAdam、SparseAdam

