机器学习-算法应用
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
机器学习-算法应用
1.线性回归
硝酸钠的溶解度试验中,测得不同温度x(单位:C)下,硝酸钠溶解于水中的溶解度y%的数据如下:
| 温度 | 4 | 10 | 15 | 21 | 29 | 36 | 51 | 68 | |
|---|---|---|---|---|---|---|---|---|---|
| 溶解度(%) | 66.7 | 71.0 | 76.3 | 80.6 | 85.7 | 92.9 | 99.4 | 113.6 | 125.1 |
(1)求y和x的线性回归函数。
(2)使用该模型预测20度时的溶解度。 $$ X=\begin{bmatrix} 1&0\ 1&4\ 1&10\ 1&15\ 1&21\ 1&29\ 1&36\ 1&51\ 1&68 \end{bmatrix} Y=\begin{bmatrix} 66.7\ 71.0 \ 76.3 \ 80.6 \ 85.7 \ 92.9 \ 99.4 \ 113.6 \ 125.1 \end{bmatrix} $$
$$ \widehat{\boldsymbol{w}}_{O L S}=\left(\boldsymbol{X}^{\mathrm{T}} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\mathrm{T}} \boldsymbol{Y}=\begin{bmatrix} 67.51\ 0.87 \end{bmatrix} $$
(1)y = 0.87x + 67.51
(2)x = 20时,y = 84.92
2.若矩阵U是正交矩阵,针对2-范数||.||,证明正交变换的保范性,即||Ux||=||x||.
$$ \left | Ux \right | = \sqrt{(Ux)^{T} Ux} = \sqrt{x^{T}U^{T} Ux} = \sqrt{x^{T}x} = \left | x \right | $$
3.将3行2列矩阵A进行SVD分解。
$$ A = \begin{bmatrix} 0&1\ 1&1\ 1&0 \end{bmatrix} $$
解:① $$ A^{T}A = \begin{bmatrix} 2&1\ 1&2 \end{bmatrix} $$ 对应的特征值,特征向量: $$ \lambda _{1} = 3,\lambda _{2} = 1 $$
$$ \overrightarrow{v_{1} }=\binom{\frac{1}{\sqrt{2} } }{\frac{1}{\sqrt{2} }} \overrightarrow{v_{2} }=\binom{-\frac{1}{\sqrt{2} } }{\frac{1}{\sqrt{2} }} $$
② $$ AA^{T} = \begin{bmatrix} 1&1&0\ 1&2&1\ 0&1&1 \end{bmatrix} $$ 对应的特征值,特征向量: $$ \lambda _{1} = 3,\lambda _{2} = 1,\lambda _{3} = 0 $$
$$ \overrightarrow{u_{1} }=\begin{pmatrix} \frac{1}{\sqrt{6} }\ \frac{2}{\sqrt{6} }\ \frac{1}{\sqrt{6} } \end{pmatrix} \overrightarrow{u_{2} }=\begin{pmatrix} \frac{1}{\sqrt{2} }\ 0\ -\frac{1}{\sqrt{2} } \end{pmatrix} \overrightarrow{u_{3} }=\begin{pmatrix} \frac{1}{\sqrt{3} }\ -\frac{1}{\sqrt{3} }\ \frac{1}{\sqrt{3} } \end{pmatrix} $$
③ $$ \sigma _{1} = \sqrt{\lambda _{1} } =\sqrt{3}, \sigma _{2} = \sqrt{\lambda _{2} } =1 $$ ④ $$ A=U\Sigma V^{T}=\begin{bmatrix} \frac{1}{\sqrt{6}}&\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{3}}\ \frac{2}{\sqrt{6}}&0&-\frac{1}{\sqrt{3}} \ \frac{1}{\sqrt{6}}&-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{3}} \end{bmatrix} \begin{bmatrix} \sqrt{3}&0\ 0&1\ 0&0 \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\ -\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}} \end{bmatrix} $$
4.感知机
(1)Minsky与Papert指出:感知机因为是线性模型,所以不能表示复杂的函数,比如异或XOR。请验证(证明)感知机不能表示异或操作。
证明
对于异或函数XOR,全部的输入与对应的输出如下:
| x(1) | x(2) | y |
|---|---|---|
| 1 | 1 | -1 |
| 1 | -1 | 1 |
| -1 | 1 | 1 |
| -1 | -1 | -1 |
假设可以有感知机可以进行异或函数的表示,即存在实数w0,w1,w2决定的线性分类面y=w0+w1x(1)+w2x(2)可以将(1,1)(1,-1)(-1,1)(-1,-1)四点按照真值表中的y值分为两类,即如下式子成立:
w0+w1+w2<0 ①
w0+w1-w2>=0 ②
w0-w1+w2>=0 ③
w0-w1-w2<0 ④
①-② 可得w2<0
③-④ 可得w2>0
显然矛盾。反证得出结论。
(2)训练数据集如下:正实例点x1=(3,3)T,x2=(4,3)T,负实例点x3=(1,1)T。试用感知机学习算法的原始形式求解感知机模型f(x)=sign(w·x+b),其中w=(w(1),w(2))T。请在如下表格中填写算法的迭代过程(步长为1)。 $$ w\longleftarrow w+\eta x_{i} y_{i} $$
$$ b\longleftarrow b+\eta y_{i} $$
| 迭代次数 | 误分类点 | w | b | wx+b |
|---|---|---|---|---|
| (0,0) | ||||
| 1 | x2 | (4,3) | 1 | 4x(1)+3x(2)+1 |
| 2 | x3 | (3,2) | 3x(1)+2x(2) | |
| 3 | x3 | (2,1) | -1 | 2x(1)+ x(2)-1 |
| 4 | x3 | (1,0) | -2 | x(1)-2 |
5.评价指标
一个模型对15个样本进行预测,结果如下。
真实值:0 1 1 0 1 1 0 0 1 0 1 0 1 0 0
预测值:1 1 1 1 1 0 0 0 0 0 1 1 1 0 1
请分别计算:(1)精度(precision)(2)召回(recall)(3)特异度(specificity)(4)F1值(F1-score)
| 预测值 = 1 | 预测值 = 0 | |
|---|---|---|
| 真实值 = 1 | 5(TP) | 2(FN) |
| 真实值 = 0 | 4(FP) | 4(TN) |
(后者表示预测的值,前者表示预测的对不对,以FP为例,表示预测值为1,且预测错误,即:01)
精度(precision, 或者PPV, positive predictive value) = TP / (TP + FP)
精度 = 5 / (5+4) = 0.556
召回(recall, 或者敏感度,sensitivity,真阳性率,TPR,True Positive Rate) = TP / (TP + FN)
召回 = 5 / (5+2) = 0.714
特异度(specificity,或者真阴性率,TNR,True Negative Rate) = TN / (TN + FP)
特异度 = 4 / (4+2) = 0.667
F1-值(F1-score) = 2TP / (2TP+FP+FN)
F1-值 = 25 / (25+4+2) = 0.625
6.人工神经网络
阅读如下神经网络结构图,图中从左至右共有两个隐层H1、H2和一个输出层O,激活函数为Sigmoid。

若输入为(1,-1),给出各层正向输出的计算过程。 $$ x_{ji}:单元j的第i个输入,w_{ji}:与x_{ji}相关联的值 $$
$$ 单元j的输入的加权和:net_{j} = x_{j1}w_{j1}+x_{j2}w_{j2}+...+x_{jn}w_{jn} $$
$$ 单元j的输出:o_{j} = f(net_{j}) = \frac{1}{1+e^{-net_{j}} } $$
(计算略)
7.朴素贝叶斯
根据如下数据,对<Outlook=sunny,Temperature=cool,Humidity=high,Wind=strong>使用朴素贝叶斯算法进行PlayTennis值的预测。其中,朴素贝叶斯算法中的参数估计使用极大似然估计方法。
 $$
P(结果_{i}|影响因素_{0-n} ) = P(结果_{i})\prod_{k=0}^n(影响因素_{i}|结果_{i} )
$$
P(yes) = 9/14
$$
P(结果_{i}|影响因素_{0-n} ) = P(结果_{i})\prod_{k=0}^n(影响因素_{i}|结果_{i} )
$$
P(yes) = 9/14
P(no) = 5/14
P(sunny|yes) = 2/9
P(sunny|no) = 3/5
P(cool|yes) = 3/9
P(cool|no) = 1/5
P(high|yes) = 3/9
P(high|no) = 3/5
P(strong|yes) = 3/9
P(strong|no) = 3/5
P1 = P(yes)P(sunny|yes) P(cool|yes) P(high|yes)P(strong|yes)
P2= P(no)P(sunny|no) P(cool|no) P(high|no)P(strong|no)
∵P1 < P2 ∴分类为no
8.聚类
给定含有5个样本的集合

(1)请用k均值聚类算法将样本聚为两类,距离度量为曼哈顿距离。
(2)请用层次聚类算法将样本聚为两类,距离度量为曼哈顿距离,类间距度量为不同类样本的最短间距。 解:
(1)
①选择两个样本点作为类1、类2的中心,类1中心m1(0)=x4=(5,0),类2中心m2(0)=x5=(-1,-1)
②以m1(0),m2(0)作为两类中心,分别计算x1,x2,x3到两类中心的曼哈顿距离。
对x1=(0,2),d(x1,m1(0))=7,d(x1,m2(0))=3,把x1分到类2。
对x2=(0,0),d(x2,m1(0))=5,d(x2,m2(0))=2,把x2分到类2。
对x3=(1,0),d(x3,m1(0))=4,d(x3,m2(0))=3,把x3分到类2。
③更新两类:类1={x4},类2={x1,x2,x3,x5},类1中心为m1(1)=(5,0),类2中心m2(1)=(0,0.25)
④重复步骤(2)、(3),将x1分到类2,x2分到类2,x3分到类2,x4分到类1,x5分到类2
⑥更新两类:类1={x4},类2={x1,x2,x3,x5},由于得到的类没有改变,聚类终止。
(2)
①首先用5个样本构建5个类,G(i)={xi},i=1,2,3,4,5。这样,样本之间的距离就是类间距,按照曼哈顿距离进行计算,得到5个类之间的距离矩阵D。
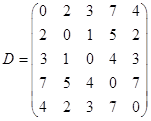
②D矩阵中D23=D32=1最小,因此合并G2、G3,记G6={x2,x3}。
③计算G6与G1、G4、G5之间的最短距离,有D61=2,D64=4,D65=2。
其他两类间距D14=7,D15=4,D45=7。 D61=D65=2最小,选择G1与G6合并,记G7={x1,x2,x3}。
④计算G7与G4、G5之间的最短距离,有D74=4,D75=2。
其他两类间距D45=7。 D75=2最小,选择G5与G7合并,记G8={x1,x2,x3,x5}。
⑤此时,所有样本分成了两类G4={x4},G8={x1,x2,x3,x5},聚类终止。
9.马氏距离
假设二维空间中有8个样本点,分成以下两类。第1类:(0,2),(-2,0),(3,5),(-3,-5),第2类:(3,5),(1,3),(8,6),(0,2)。请计算两类样本的均值与协方差矩阵,计算(0,2)与(3,5)分别在两类中的马氏距离。
解: $$ X = \begin{bmatrix} x_{1}&x_{2}&...&x_{n} \end{bmatrix}= \begin{bmatrix} 0& -2& 3& -3\ 2& 0& 5& -5 \end{bmatrix} $$
$$ Y = \begin{bmatrix} y_{1}&y_{2}&...&y_{m} \end{bmatrix}= \begin{bmatrix} 3& 1& 8& 0\ 5& 3& 6& 2 \end{bmatrix} $$
$$ \overline{X} = \begin{bmatrix} -0.5\0.5\end{bmatrix}, \overline{Y} = \begin{bmatrix} 3\4\end{bmatrix} $$
$$ X' = X - [\overline{X},\overline{X}…], Y' = Y - [\overline{Y},\overline{Y}…] $$
$$ covX = \frac{1}{n-1}X'X'^{T}= \begin{bmatrix} 7& 10.33\ 10.33&17.66 \end{bmatrix} $$
$$ covY = \frac{1}{m-1}Y'Y'^{T}= \begin{bmatrix} 12.67& 6\ 6&3.33 \end{bmatrix} $$
$$ MD_{X}(\overrightarrow{u},\overrightarrow{v})= \sqrt{(\overrightarrow{u}-\overrightarrow{v})^{T} covX^{-1}(\overrightarrow{u}-\overrightarrow{v})}=1.46 $$
$$ MD_{Y}(\overrightarrow{u},\overrightarrow{v})= \sqrt{(\overrightarrow{u}-\overrightarrow{v})^{T} covY^{-1}(\overrightarrow{u}-\overrightarrow{v})}=2.41 $$
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

