李宏毅机器学习笔记.Flow-based Generative Model(补)-CSDN博客
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
文章目录
原视频见油管https://www.youtube.com/watch?v=uXY18nzdSsM
Latex编辑器
引子
之前有讲过三种生成模型
1.Component-by-component (也叫Auto-regressive Model)按component进行生成如何确定最佳的生成顺序而且一个个的生成会使得速度比较慢。特别是语音生成一秒钟需要生成的采样点个数约为20万个有人声称生成一秒钟合成90分。
2.AutoencoderVAE这个模型证明了是在优化似然的Lower bound而非去maximize似然这样的效果有多好还不好说。
3.Generative Adversarial Network(GAN)虽然很强但是很难训练。
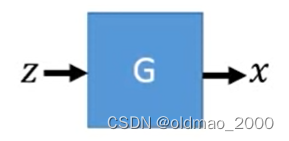
生成问题回顾Generator
A generator
G
G
G is a network. The network defines a probability distribution
p
G
p_G
pG
为什么说生成器网络定义了一个概率分布看下面的流程
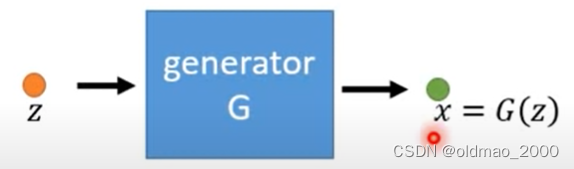
图中
G
G
G吃一个向量
z
z
z得到一个表示
x
=
G
(
z
)
x=G(z)
x=G(z)这个
x
x
x是一个高维向量是一张图像
x
x
x里面每一个维度就是这个图像的每一个像素。
输入向量
z
z
z是用一个Normal Distribution中采样得来的
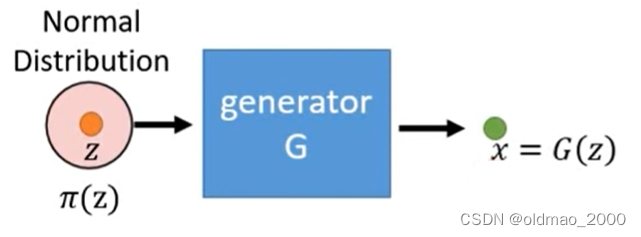
因此经过多次采样经过
G
G
G后会得到一个比较复杂的分布
p
G
p_G
pG
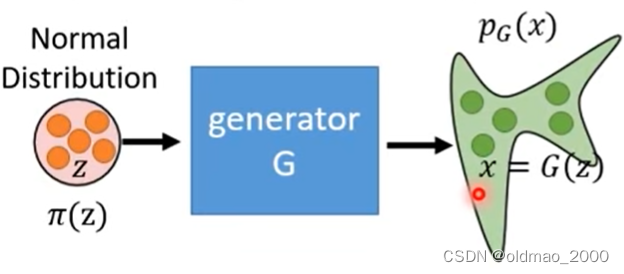
我们希望找到一个
G
G
G使得其生成的分布
p
G
p_G
pG与实际图像分布
p
d
a
t
a
(
x
)
p_{data}(x)
pdata(x)越接近越好。
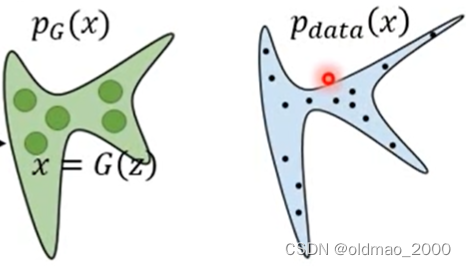
越接近越好就是要求最大似然也就是要使得
p
G
(
x
)
p_G(x)
pG(x)的似然与
p
d
a
t
a
(
x
)
p_{data}(x)
pdata(x)采样得到的样本越接近越好用数学表示为
G
∗
=
a
r
g
max
G
∑
i
=
1
m
log
p
G
(
x
i
)
,
{
x
1
,
x
2
,
⋯
,
x
m
}
f
r
o
m
p
d
a
t
a
(
x
)
≈
a
r
g
min
G
K
L
(
p
d
a
t
a
∣
∣
p
G
)
\begin{aligned} G^*&=arg\max_G\sum_{i=1}^{m}\log p_G(x^i),\{x^1,x^2,\cdots,x^m\}\text{ } from\text{ } p_{data}(x)\\ &\approx arg\min_G KL(p_{data}||p_G)\end{aligned}
G∗=argGmaxi=1∑mlogpG(xi),{x1,x2,⋯,xm} from pdata(x)≈argGminKL(pdata∣∣pG)
上式中的求两个概率越接近越好也相当于求他们的KL散度越小越好。
由于
G
G
G是一个网络因此其生成概率的最大似然非常难求Flow-based Generative Model提出了一种可以直接求最大似然的方法接下来进入难点补充部分数学推导。
Math Background
三个东西Jacobian, Determinant, Change of Variable Theorem
Jacobian Matrix
假如有一个函数
x
=
f
(
z
)
x=f(z)
x=f(z)吃一个二维向量
z
=
[
z
1
z
2
]
z=\begin{bmatrix} z_1 \\ z_2 \end{bmatrix}
z=[z1z2]得到输出
x
=
[
x
1
x
2
]
x=\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}
x=[x1x2]。Jacobian Matrix的输入和输出维度不一定一样这里先简化来举例
这里的函数可以看做上面提到的生成器
G
G
G。
函数
x
=
f
(
z
)
x=f(z)
x=f(z)的Jacobian Matrix
J
f
J_f
Jf可以写为输入和输出两两组合做偏导后形成的矩阵
J
f
=
[
∂ x
1
∂ z
1
∂ x
1
∂ z
2
∂ x
2
∂ z
1
∂ x
2
∂ z
2
]
(1)
J_f=\begin{bmatrix} \cfrac{\partial x_1}{\partial z_1} & \cfrac{\partial x_1}{\partial z_2}\\ \cfrac{\partial x_2}{\partial z_1} &\cfrac{\partial x_2}{\partial z_2} \end{bmatrix}\tag1
Jf=
∂z1∂x1∂z1∂x2∂z2∂x1∂z2∂x2
(1)
Jacobian Matrix小例子假如有这样的函数
[
z
1
+
z
2
2
z
2
]
=
f
(
[
z
1
z
2
]
)
\begin{bmatrix} z_1+z_2 \\ 2z_2 \end{bmatrix}=f\left(\begin{bmatrix} z_1 \\ z_2 \end{bmatrix}\right)
[z1+z22z2]=f([z1z2])
则根据上面的公式1可以求得
J
f
=
[
∂
(
z
1
+
z
2
)
∂
z
1
∂
(
z
1
+
z
2
)
∂
z
2
∂
2
z
2
∂
z
1
∂
2
z
2
∂
z
2
]
=
[
1
1
2
0
]
J_f=\begin{bmatrix} \cfrac{\partial (z_1+z_2)}{\partial z_1} & \cfrac{\partial (z_1+z_2)}{\partial z_2}\\ \cfrac{\partial 2z_2}{\partial z_1} &\cfrac{\partial 2z_2}{\partial z_2} \end{bmatrix}=\begin{bmatrix} 1 & 1\\ 2 &0 \end{bmatrix}
Jf=
∂z1∂(z1+z2)∂z1∂2z2∂z2∂(z1+z2)∂z2∂2z2
=[1210]
同理若有
z
=
f
−
1
(
x
)
z=f^{-1}(x)
z=f−1(x)则有函数
f
f
finverse 的Jacobian Matrix
J
f
−
1
=
[
∂ z
1
∂ x
1
∂ z
1
∂ x
2
∂ z
2
∂ x
1
∂ z
2
∂ x
2
]
(2)
J_{f^{-1}}=\begin{bmatrix} \cfrac{\partial z_1}{\partial x_1} & \cfrac{\partial z_1}{\partial x_2}\\ \cfrac{\partial z_2}{\partial x_1} &\cfrac{\partial z_2}{\partial x_2} \end{bmatrix}\tag2
Jf−1=
∂x1∂z1∂x1∂z2∂x2∂z1∂x2∂z2
(2)
公式1和2的两个矩阵互逆二者的乘积结果是Identity矩阵对角线是1其他都是0。
反函数的Jacobian Matrix小例子假如有这样的函数
[
x
2
/
2
x
1
−
x
2
/
2
]
=
f
−
1
(
[
x
1
x
2
]
)
\begin{bmatrix} x_2/2 \\ x_1-x_2/2 \end{bmatrix}=f^{-1}\left(\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\right)
[x2/2x1−x2/2]=f−1([x1x2])
则根据上面的公式2可以求得
J
f
−
1
=
[
∂
(
x
2
/
2
)
∂
x
1
∂
(
x
2
/
2
)
∂
x
2
∂
(
x
1
−
x
2
/
2
)
∂
x
1
∂
(
x
1
−
x
2
/
2
)
∂
x
2
]
=
[
0
1
/
2
1
−
1
/
2
]
J_{f^{-1}}=\begin{bmatrix} \cfrac{\partial (x_2/2)}{\partial x_1} & \cfrac{\partial (x_2/2)}{\partial x_2}\\ \cfrac{\partial (x_1-x_2/2)}{\partial x_1} &\cfrac{\partial (x_1-x_2/2)}{\partial x_2} \end{bmatrix}=\begin{bmatrix} 0 & 1/2\\ 1 &-1/2 \end{bmatrix}
Jf−1=
∂x1∂(x2/2)∂x1∂(x1−x2/2)∂x2∂(x2/2)∂x2∂(x1−x2/2)
=[011/2−1/2]
两个小例子的结果相乘
J
f
J
f
−
1
=
[
1
1
2
0
]
[
0
1
/
2
1
−
1
/
2
]
=
I
J_fJ_{f^{-1}}=\begin{bmatrix} 1 & 1\\ 2 &0 \end{bmatrix}\begin{bmatrix} 0 & 1/2\\ 1 &-1/2 \end{bmatrix}=I
JfJf−1=[1210][011/2−1/2]=I
Determinant 行列式
The determinant of a square matrix is a scalar that provides information about the matrix.
对于2×2的矩阵
A
=
[
a
b
c
d
]
A=\begin{bmatrix} a&b \\ c &d \end{bmatrix}
A=[acbd]
有
d
e
t
(
A
)
=
a
d
−
b
c
det(A)=ad-bc
det(A)=ad−bc
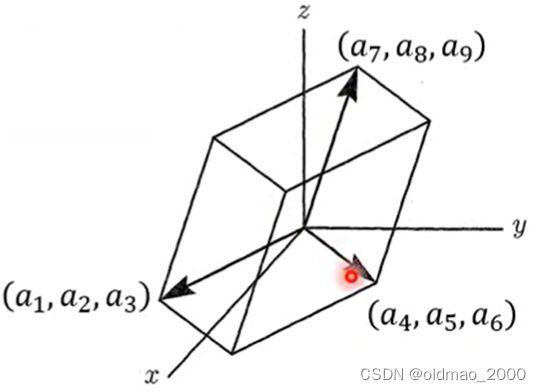
对于3×3的矩阵
[
a
1
a
2
a
3
a
4
a
5
a
6
a
7
a
8
a
9
]
\begin{bmatrix} a_1 & a_2& a_3\\ a_4 & a_ 5&a_6 \\ a_7 & a_8 &a_9 \end{bmatrix}
a1a4a7a2a5a8a3a6a9
有
d
e
t
(
A
)
=
a
1
a
5
a
9
+
a
2
a
6
a
7
+
a
3
a
4
a
8
−
a
3
a
5
a
7
−
a
2
a
4
a
9
−
a
1
a
6
a
8
det(A)=a_1a_5a_9+a_2a_6a_7+a_3a_4a_8-a_3a_5a_7-a_2a_4a_9-a_1a_6a_8
det(A)=a1a5a9+a2a6a7+a3a4a8−a3a5a7−a2a4a9−a1a6a8
行列式性质
d
e
t
(
A
)
=
1
d
e
t
(
A
−
1
)
det(A)=\cfrac{1}{det(A^{-1})}
det(A)=det(A−1)1
对于Jacobian Matrix则有
d
e
t
(
J
f
)
=
1
d
e
t
(
J
f
−
1
)
det(J_f)=\cfrac{1}{det(J_{f^{-1}})}
det(Jf)=det(Jf−1)1
行列式的几何含义是指行向量在高维空间形成的体积。对于低维例如下面2×2的矩阵其行列式就对应了其行向量所形成的面积

对于3×3的矩阵其行列式就对应了其行向量所形成的体积
Change of Variable Theorem
变量变换定理。
简单实例
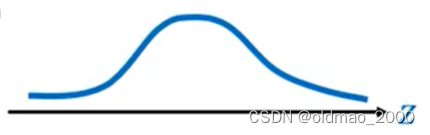
假设有分布
π
(
z
)
\pi(z)
π(z)其图像如下
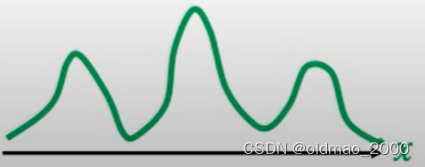
另有函数可以以上面的分布作为输入
x
=
f
(
z
)
x=f(z)
x=f(z)得到的结果是另外一个分布
p
(
x
)
p(x)
p(x)其图像如下
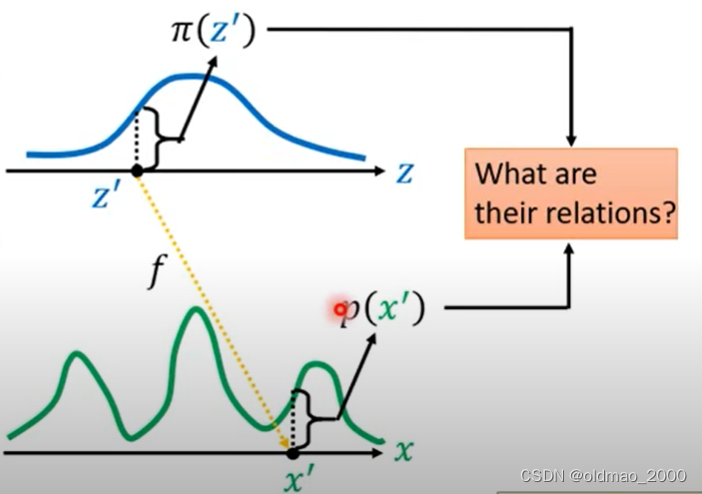
现在要弄清楚
π
(
z
)
\pi(z)
π(z)和
p
(
x
)
p(x)
p(x)两个分布之间的关系。
下面来看简单的例子假设分布
π
(
z
)
\pi(z)
π(z)如下图
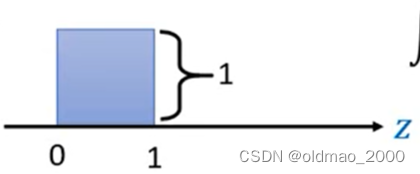
可以看到
π
(
z
)
\pi(z)
π(z)是一个简单的均匀分布它在0~1之间有分布。根据概率的定义
∫
0
1
π
(
z
)
d
z
=
1
\int_0^1\pi(z)dz=1
∫01π(z)dz=1
因此可以知道该分布的高度为1。
令假设有函数
x
=
f
(
z
)
=
2
z
+
1
x=f(z)=2z+1
x=f(z)=2z+1
则可以得到函数生成的分布
p
(
x
)
p(x)
p(x)的图像为
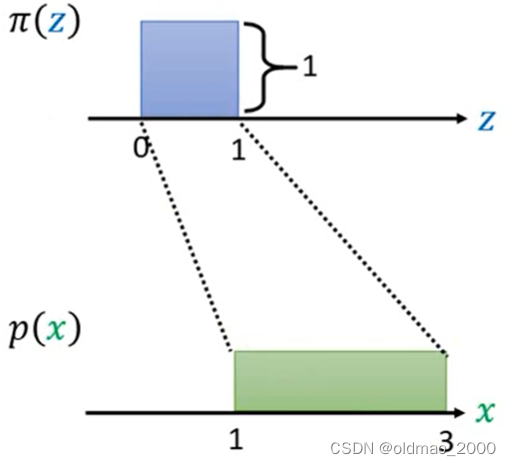
由于
p
(
x
)
p(x)
p(x)是概率分布因此其也要满足
∫
1
3
p
(
x
)
d
x
=
1
\int_1^3p(x)dx=1
∫13p(x)dx=1
则绿色分布的高度为0.5则可以德奥两个分布之间的关系
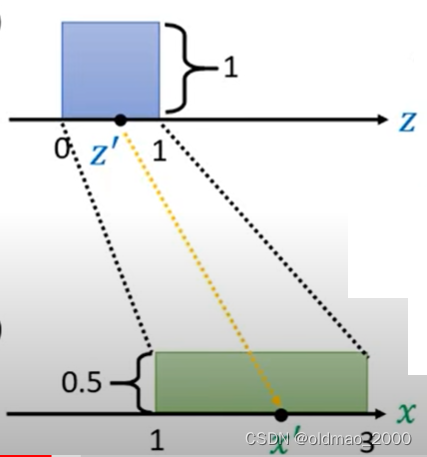
可以写成
p
(
x
′
)
=
1
2
π
(
z
′
)
p(x')=\cfrac{1}{2}\pi(z')
p(x′)=21π(z′)
一维实例
下面再推广到更一般的情况。
现在有一个分布记为
π
(
z
)
\pi(z)
π(z)它经过一个变换或者按上面的说法经过一个函数后得到另外一个分布
p
(
x
)
p(x)
p(x)对于下图而言
z
′
z'
z′通过变换后就到
x
′
x'
x′的位置对应的概率密度从
π
(
z
′
)
\pi(z')
π(z′)变成了
p
(
x
′
)
p(x')
p(x′)。
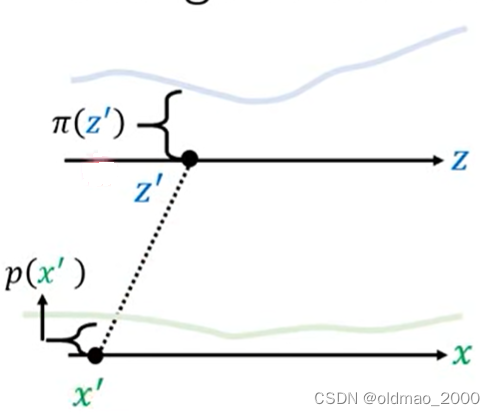
虽然我们不知道
π
(
z
)
\pi(z)
π(z)和
p
(
x
)
p(x)
p(x)具体的公式但是我们如果知道变换所涉及的函数是可以写出二者的关系的这就是通过Change of Variable Theorem来找到这个关系的过程。
先将
z
′
z'
z′做一个小小的变动成为
z
′
+
Δ
z
z'+\Delta z
z′+Δz相应的根据变换函数可以得到对应的
x
′
+
Δ
x
x'+\Delta x
x′+Δx
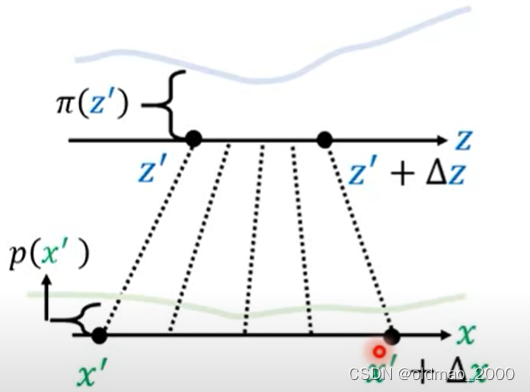
由于我们做的小小的变动因此从
z
′
z'
z′到
z
′
+
Δ
z
z'+\Delta z
z′+Δz对应的概率密度可以看做是均匀分布同理从
x
′
x'
x′到
x
′
+
Δ
x
x'+\Delta x
x′+Δx应的概率密度也可以看做是均匀分布
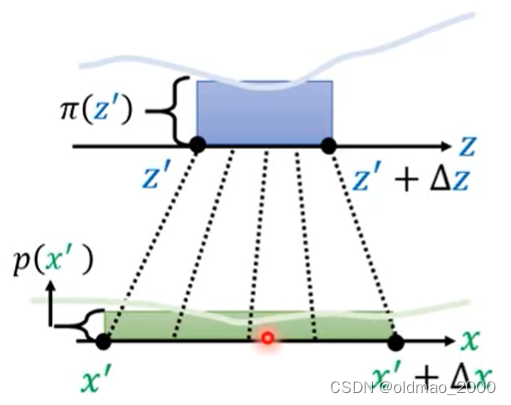
相当于将蓝色方块经过变形得到绿色方块二者的面积是相等的二者长×宽应该结果一样。即
p
(
x
′
)
Δ
x
=
π
(
z
′
)
Δ
z
p(x')\Delta x=\pi(z')\Delta z
p(x′)Δx=π(z′)Δz
移项办得到二者的关系可以写为
p
(
x
′
)
=
π
(
z
′
)
Δ
z
Δ
x
p(x')=\pi(z')\cfrac{\Delta z}{\Delta x}
p(x′)=π(z′)ΔxΔz
由于
Δ
\Delta
Δ是很小的值因此根据导数的概念上式可以写为
p
(
x
′
)
=
π
(
z
′
)
d
z
d
x
p(x')=\pi(z')\cfrac{d z}{d x}
p(x′)=π(z′)dxdz
由于上面的求导项可能有正负
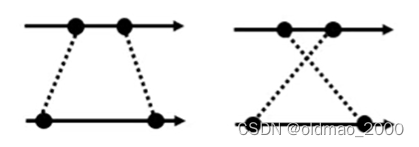
因此要加上绝对值避免负值
p
(
x
′
)
=
π
(
z
′
)
∣
d
z
d
x
∣
p(x')=\pi(z')\left|\cfrac{d z}{d x}\right|
p(x′)=π(z′)
dxdz
二维实例
对于二维的情况
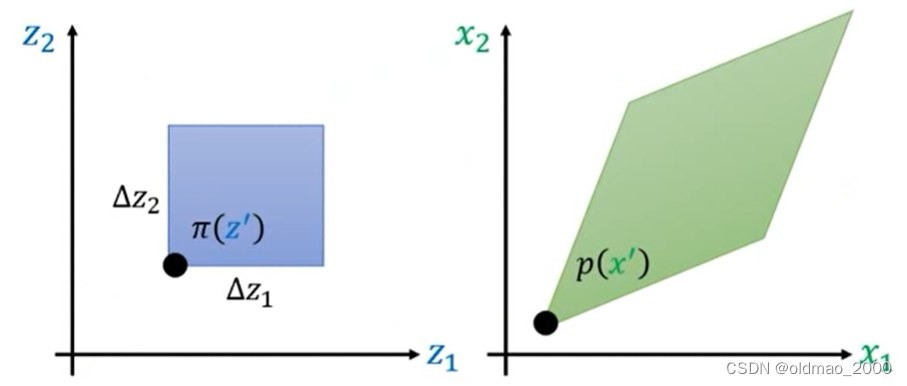
同样的现在有一个分布记为
π
(
z
)
\pi(z)
π(z)它经过一个变换后得到另外一个分布
p
(
x
)
p(x)
p(x)对于下图而言
z
′
z'
z′通过变换后就到
x
′
x'
x′的位置对应的概率密度从
π
(
z
′
)
\pi(z')
π(z′)变成了
p
(
x
′
)
p(x')
p(x′)。
还是给
z
′
z'
z′做一个小小的变动蓝色方形和绿色菱形的对应的概率密度体积应该相等。这里的体积就是底面积×概率密度蓝色底面积好求绿色菱形底面积用上面的行列式的几何概念来求可以看到下图中菱形可以写为成两个向量的表示
[
Δ
x
11
,
Δ
x
21
]
[\Delta x_{11}, \Delta x_{21}]
[Δx11,Δx21]
[
Δ
x
12
,
Δ
x
22
]
[\Delta x_{12},\Delta x_{22}]
[Δx12,Δx22]。

最后就是写成
p
(
x
′
)
∣
d
e
t
[
Δ
x
11
Δ
x
21
Δ
x
12
Δ
x
22
]
∣
=
π
(
z
′
)
Δ
z
1
Δ
z
2
(3)
p(x')\left| det\begin{bmatrix} \Delta x_{11}&\Delta x_{21} \\ \Delta x_{12} &\Delta x_{22} \end{bmatrix} \right|=\pi(z')\Delta z_{1}\Delta z_{2}\tag3
p(x′)
det[Δx11Δx12Δx21Δx22]
=π(z′)Δz1Δz2(3)
下面开始数学上的化简假设变换函数为
x
=
f
(
z
)
x=f(z)
x=f(z)则公式3可以写为
p
(
x
′
)
∣
1
Δ
z
1
Δ
z
2
d
e
t
[
Δ
x
11
Δ
x
21
Δ
x
12
Δ
x
22
]
∣
=
π
(
z
′
)
p(x')\left|\cfrac{1}{\Delta z_{1}\Delta z_{2}} det\begin{bmatrix} \Delta x_{11}&\Delta x_{21} \\ \Delta x_{12} &\Delta x_{22} \end{bmatrix} \right|=\pi(z')
p(x′)
Δz1Δz21det[Δx11Δx12Δx21Δx22]
=π(z′)
根据线代的指数将分数项放入行列式
p
(
x
′
)
∣
d
e
t
[
Δ
x
11
Δ
z
1
Δ
x
21
Δ
z
1
Δ
x
12
Δ
z
2
Δ
x
22
Δ
z
2
]
∣
=
π
(
z
′
)
p(x')\left|det\begin{bmatrix} \cfrac{\Delta x_{11}}{\Delta z_1} &\cfrac{\Delta x_{21}}{\Delta z_1} \\ \cfrac{\Delta x_{12}}{\Delta z_2} &\cfrac{\Delta x_{22}}{\Delta z_2} \end{bmatrix} \right|=\pi(z')
p(x′)
det
Δz1Δx11Δz2Δx12Δz1Δx21Δz2Δx22
=π(z′)
由于
Δ
x
11
\Delta x_{11}
Δx11是
Δ
z
1
\Delta z_{1}
Δz1在
x
1
x_1
x1上的改变量
Δ
x
21
\Delta x_{21}
Δx21是
Δ
z
1
\Delta z_{1}
Δz1在
x
2
x_2
x2上的改变量
Δ
x
12
\Delta x_{12}
Δx12是
Δ
z
2
\Delta z_{2}
Δz2在
x
1
x_1
x1上的改变量
Δ
x
22
\Delta x_{22}
Δx22是
Δ
z
2
\Delta z_{2}
Δz2在
x
2
x_2
x2上的改变量。
上面的式子可以写成
p
(
x
′
)
∣
d
e
t
[
∂
x
1
∂
z
1
∂
x
2
∂
z
1
∂
x
1
∂
z
2
∂
x
2
∂
z
2
]
∣
=
π
(
z
′
)
p(x')\left|det\begin{bmatrix} \cfrac{\partial x_{1}}{\partial z_1} &\cfrac{\partial x_{2}}{\partial z_1} \\ \cfrac{\partial x_{1}}{\partial z_2} &\cfrac{\partial x_{2}}{\partial z_2} \end{bmatrix} \right|=\pi(z')
p(x′)
det
∂z1∂x1∂z2∂x1∂z1∂x2∂z2∂x2
=π(z′)
将矩阵进行Transpose不会改变行列式的值上式可以写成
p
(
x
′
)
∣
d
e
t
[
∂
x
1
∂
z
1
∂
x
1
∂
z
2
∂
x
2
∂
z
1
∂
x
2
∂
z
2
]
∣
=
π
(
z
′
)
p(x')\left|det\begin{bmatrix} \cfrac{\partial x_{1}}{\partial z_1} &\cfrac{\partial x_{1}}{\partial z_2} \\ \cfrac{\partial x_{2}}{\partial z_1} &\cfrac{\partial x_{2}}{\partial z_2} \end{bmatrix} \right|=\pi(z')
p(x′)
det
∂z1∂x1∂z1∂x2∂z2∂x1∂z2∂x2
=π(z′)
上面行列式中的句子和公式1中的Jacobian Matrix形式一样因此可以写成
p
(
x
′
)
∣
d
e
t
(
J
f
)
∣
=
π
(
z
′
)
(4)
p(x')\left|det(J_f) \right|=\pi(z')\tag4
p(x′)∣det(Jf)∣=π(z′)(4)
也可以写为
p
(
x
′
)
=
π
(
z
′
)
∣
1
d
e
t
(
J
f
)
∣
=
π
(
z
′
)
∣
d
e
t
(
J
f
−
1
)
∣
(5)
p(x')=\pi(z')\left|\cfrac{1}{det(J_f) }\right|=\pi(z')|det(J_{f^{-1}})| \tag5
p(x′)=π(z′)
det(Jf)1
=π(z′)∣det(Jf−1)∣(5)
网络G的限制
先把上面最大似然的式子copy下来
G
∗
=
a
r
g
max
G
∑
i
=
1
m
log
p
G
(
x
i
)
,
{
x
1
,
x
2
,
⋯
,
x
m
}
f
r
o
m
P
d
a
t
a
(
x
)
G^*=arg\max_G\sum_{i=1}^{m}\log p_G(x^i),\{x^1,x^2,\cdots,x^m\}\text{ } from\text{ } P_{data}(x)
G∗=argGmaxi=1∑mlogpG(xi),{x1,x2,⋯,xm} from Pdata(x)
根据上面公式5可以把
p
G
p_G
pG写成
p
G
(
x
i
)
=
π
(
z
i
)
∣
d
e
t
(
J
G
−
1
)
∣
p_G(x^i)=\pi (z^i)|det(J_{G^{-1}})|
pG(xi)=π(zi)∣det(JG−1)∣
由已知的
x
=
G
(
z
)
x=G(z)
x=G(z)可以得其反函数为
z
i
=
G
−
1
(
x
i
)
z^i=G^{-1}(x^i)
zi=G−1(xi)带入上式
p
G
(
x
i
)
=
π
(
G
−
1
(
x
i
)
)
∣
d
e
t
(
J
G
−
1
)
∣
p_G(x^i)=\pi \left(G^{-1}(x^i)\right )\left|det(J_{G^{-1}})\right |
pG(xi)=π(G−1(xi))∣det(JG−1)∣
两边同时取对数然后乘变加展开
log
p
G
(
x
i
)
=
log
[
π
(
G
−
1
(
x
i
)
)
∣
d
e
t
(
J
G
−
1
)
∣
]
=
log
(
G
−
1
(
x
i
)
)
+
log
∣
d
e
t
(
J
G
−
1
)
∣
\begin{aligned} \log p_G(x^i)&=\log \left[\pi \left(G^{-1}(x^i)\right )\left|det(J_{G^{-1}})\right |\right]\\ &= \log \left(G^{-1}(x^i)\right )+\log\left|det(J_{G^{-1}})\right |\end{aligned}
logpG(xi)=log[π(G−1(xi))∣det(JG−1)∣]=log(G−1(xi))+log∣det(JG−1)∣
要求
G
∗
G^*
G∗就是要求上式的最大值如果要想用GD来求解必须要计算两个东西
1.
d
e
t
(
J
G
−
1
)
或
d
e
t
(
J
G
)
det(J_{G^{-1}})或det(J_{G})
det(JG−1)或det(JG)这个还比较好算就是要计算输入
z
z
z和输出
x
x
x的偏导即可但是如果输入和输出各自有1000维由于Jacobian Matrix是输入输出的各个维度的两两偏导其大小就是1000×1000这个大小的矩阵求行列式的值计算量会很大。
2.
G
−
1
G^{-1}
G−1主要是要确保
G
G
G有反函数由于
G
G
G是一个网络因此其构架要精心设计才会有反函数。
根据上面的两点如果要输出一张100×100×3的图片那么输入也要100×100×3这个是确保
G
G
G有反函数的必要条件。
显然网络
G
G
G不可以是简单的、任意的类似CNN、RNN等网络架构于是就有了流式设计。
基于Flow的网络构架
一个网络
G
G
G不够因此考虑像流水一样设计多个网络进行concat

根据上面的公式这些网络之间的输入输出关系如下
p
1
(
x
i
)
=
π
(
z
i
)
(
∣
d
e
t
(
J
G
1
−
1
)
∣
)
p
2
(
x
i
)
=
π
(
z
i
)
(
∣
d
e
t
(
J
G
1
−
1
)
∣
)
(
∣
d
e
t
(
J
G
2
−
1
)
∣
)
⋮
p
K
(
x
i
)
=
π
(
z
i
)
(
∣
d
e
t
(
J
G
1
−
1
)
∣
)
⋯
(
∣
d
e
t
(
J
G
K
−
1
)
∣
)
\begin{aligned} p_1(x^i)&=\pi \left(z^i\right )\left(\left|det(J_{G^{-1}_1})\right |\right )\\ p_2(x^i)&=\pi \left(z^i\right )\left(\left|det(J_{G^{-1}_1})\right |\right )\left(\left|det(J_{G^{-1}_2})\right |\right )\\ &\quad\vdots\\ p_K(x^i)&=\pi \left(z^i\right )\left(\left|det(J_{G^{-1}_1})\right |\right )\cdots\left(\left|det(J_{G^{-1}_K})\right |\right ) \end{aligned}
p1(xi)p2(xi)pK(xi)=π(zi)(
det(JG1−1)
)=π(zi)(
det(JG1−1)
)(
det(JG2−1)
)⋮=π(zi)(
det(JG1−1)
)⋯(
det(JGK−1)
)
两边同时取对数乘变加
log
p
K
(
x
i
)
=
log
π
(
z
i
)
+
∑
h
=
1
K
log
∣
d
e
t
(
J
G
K
−
1
)
∣
(6)
\log p_K(x^i)=\log \pi \left(z^i\right )+\sum_{h=1}^K\log\left|det(J_{G^{-1}_K})\right |\tag6
logpK(xi)=logπ(zi)+h=1∑Klog
det(JGK−1)
(6)
其中
z
i
=
G
1
−
1
(
⋯
G
K
−
1
(
x
i
)
)
z^i=G^{-1}_1\left(\cdots G^{-1}_K\left(x^i\right )\right )
zi=G1−1(⋯GK−1(xi))
现在要求的就是公式6的最大化。
G的训练
为了求公式6的最大化这里先简化一下问题先考虑只有一个
G
G
G情况
此时需要最大化的式子为
log
p
G
(
x
i
)
=
log
π
(
G
−
1
(
x
i
)
)
+
log
∣
d
e
t
(
J
G
−
1
)
∣
(7)
\log p_G(x^i)=\log \pi \left(G^{-1}\left(x^i\right )\right )+\log\left|det(J_{G^{-1}})\right |\tag7
logpG(xi)=logπ(G−1(xi))+log∣det(JG−1)∣(7)
式子中只有出现
G
−
1
G^{-1}
G−1因此可以训练一个
G
−
1
G^{-1}
G−1对应的网络训练好后将其输入输出反过来就变成了
G
G
G。
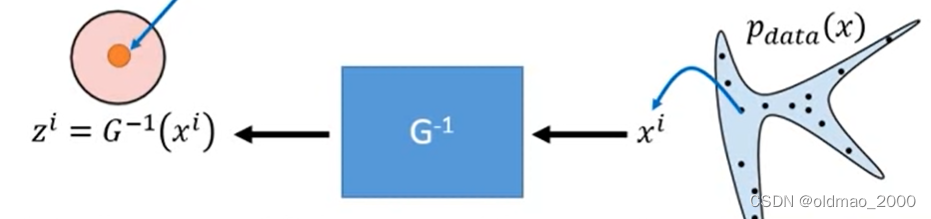
具体训练过程是从真实数据
p
d
a
t
a
(
x
)
p_{data}(x)
pdata(x)中采样一些样本
x
i
x^i
xi出来丢进
G
−
1
G^{-1}
G−1对应的网络得到对应的
z
i
z^i
zi
先看公式7中的前半部分
log
π
(
G
−
1
(
x
i
)
)
\log \pi \left(G^{-1}\left(x^i\right )\right )
logπ(G−1(xi))
这里的
π
\pi
π是正态分布也就是当
z
i
=
G
−
1
(
x
i
)
=
0
z^i=G^{-1}\left(x^i\right )=0
zi=G−1(xi)=0的时候正态分布
π
\pi
π会得到最大值正态分布最正中的地方就是波峰
如果
z
i
z^i
zi趋向于0或者说0向量的时候其对应的Jacobian Matrix
J
G
−
1
J_{G^{-1}}
JG−1也会是0矩阵因为该矩阵每个元素都是要求
z
z
z对
x
x
x的偏导0矩阵的行列式
d
e
t
(
J
G
−
1
)
=
0
det(J_{G^{-1}})=0
det(JG−1)=0再取对数会使得公式7中的后半部分趋向于负无穷大。
总之就是一项要使得
z
i
z^i
zi趋向于0后一项使得
z
i
z^i
zi不为0。
Coupling Layer
Coupling Layer反函数计算
这个设计可以参考两篇文章NICE: Non-linear Independent Components Estimation、Density estimation using Real NVP
具体结构如下图
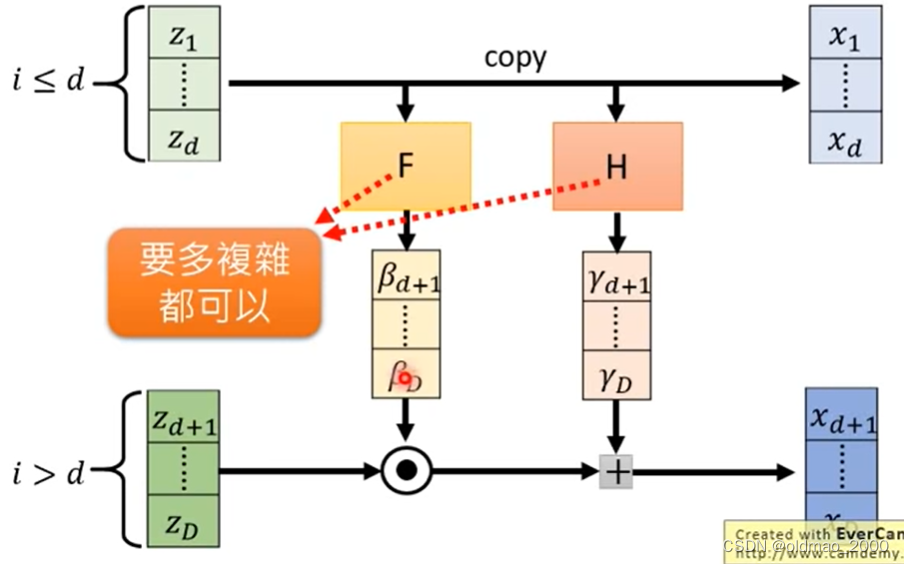
假设
z
z
z是
D
D
D维先将其分成两部分分别是
z
1
,
⋯
,
z
d
z_1,\cdots,z_d
z1,⋯,zd和
z
d
+
1
,
⋯
,
z
D
z_{d+1},\cdots,z_D
zd+1,⋯,zD。
1.将
z
z
z的第一部分
z
1
,
⋯
,
z
d
z_1,\cdots,z_d
z1,⋯,zd直接复制成为
x
x
x的第一部分
x
1
,
⋯
,
x
d
x_1,\cdots,x_d
x1,⋯,xd
2.将
z
z
z的第一部分
z
1
,
⋯
,
z
d
z_1,\cdots,z_d
z1,⋯,zd分别丢进两个网络
F
F
F和
H
H
H两个网络没有invertiable的限制可以是深度CNN分别得到
β
d
+
1
,
⋯
,
β
D
\beta_{d+1},\cdots,\beta_D
βd+1,⋯,βD和
γ
d
+
1
,
⋯
,
γ
D
\gamma_{d+1},\cdots,\gamma_D
γd+1,⋯,γD
3.将
z
z
z的第二部分
z
d
+
1
,
⋯
,
z
D
z_{d+1},\cdots,z_D
zd+1,⋯,zD先和
β
d
+
1
,
⋯
,
β
D
\beta_{d+1},\cdots,\beta_D
βd+1,⋯,βD点积然后再加上
γ
d
+
1
,
⋯
,
γ
D
\gamma_{d+1},\cdots,\gamma_D
γd+1,⋯,γD得到
x
x
x的第二部分
x
d
+
1
,
⋯
,
x
D
x_{d+1},\cdots,x_D
xd+1,⋯,xD
x
i
>
d
=
β
i
z
i
+
γ
i
x_{i>d}=\beta_iz_i+\gamma_i
xi>d=βizi+γi
Coupling Layer之所以这样设计就是可以计算反函数现在利用
x
x
x来算
z
z
z看下图的红线及序号
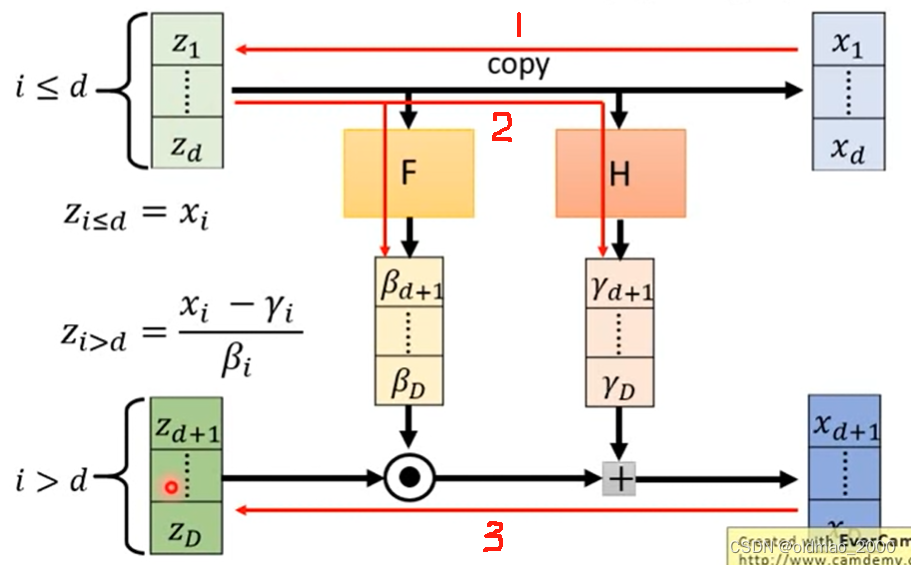
1.将
x
x
x的第一部分
x
1
,
⋯
,
x
d
x_1,\cdots,x_d
x1,⋯,xd直接复制成为
z
z
z的第一部分
z
1
,
⋯
,
z
d
z_1,\cdots,z_d
z1,⋯,zd
2.和上面的步骤2一样将
z
z
z的第一部分
z
1
,
⋯
,
z
d
z_1,\cdots,z_d
z1,⋯,zd分别丢进两个网络
F
F
F和
H
H
H分别得到
β
d
+
1
,
⋯
,
β
D
\beta_{d+1},\cdots,\beta_D
βd+1,⋯,βD和
γ
d
+
1
,
⋯
,
γ
D
\gamma_{d+1},\cdots,\gamma_D
γd+1,⋯,γD
3.根据以下公式计算
z
i
>
d
z_{i>d}
zi>d
z
i
>
d
=
x
i
−
γ
i
β
i
z_{i>d}=\cfrac{x_i-\gamma_i}{\beta_i}
zi>d=βixi−γi
Coupling Layer Jacobian矩阵计算
先把上面的Coupling Layer 结构简化成下面的样子注意颜色
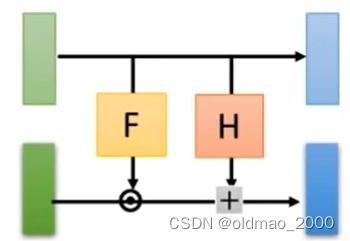
将Jacobian矩阵的计算结果分为四个部分这里的颜色和上面的简化模型颜色是对应的
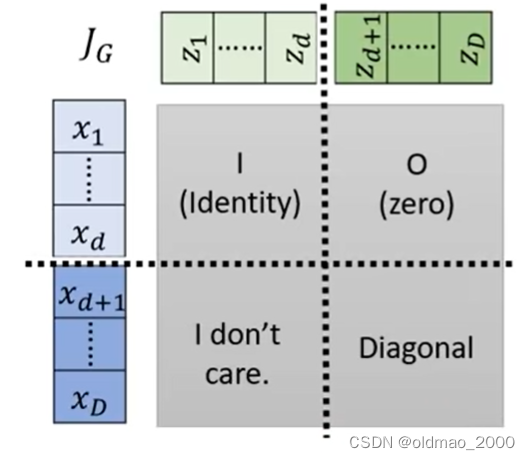
左上角是Identity矩阵因为这里
x
i
<
d
=
z
i
<
d
x_{i<d}=z_{i<d}
xi<d=zi<d浅蓝对浅绿的偏导结果除了对角线其他位置都是0
右上角结果是0因为这里浅蓝部分
x
1
,
⋯
,
x
d
x_1,\cdots,x_d
x1,⋯,xd与深绿部分
z
d
+
1
,
⋯
,
z
D
z_{d+1},\cdots,z_D
zd+1,⋯,zD无关求偏导后均为0
左下角的内容不需要考虑因为左上角是Identity矩阵和右上角是0整个灰色大矩阵的行列式的值等于右下角的行列式的值这个是行列式的某个推论
右下角就是要看深绿和深蓝部分的关系他们的关系在上面有写
x
i
>
d
=
β
i
z
i
+
γ
i
(8)
x_{i>d}=\beta_iz_i+\gamma_i\tag8
xi>d=βizi+γi(8)
从这个式子可以看到
x
d
+
1
x_{d+1}
xd+1只与
z
d
+
1
z_{d+1}
zd+1有关与
z
d
+
2
,
⋯
,
z
D
z_{d+2},\cdots,z_D
zd+2,⋯,zD无关因此右下角只有对角线上有值但不为1是一个对角线矩阵。
现在问题变成要求右下角矩阵行列式的值由于右下角是一个对角线矩阵因此其行列式的值等于对角线上的所有值的乘积行列式定义简单推导即可得到该结论可写为
d
e
t
(
J
G
)
=
∂
x
d
+
1
∂
z
d
+
1
∂
x
d
+
2
∂
z
d
+
2
⋯
∂
x
D
∂
z
D
det(J_G)=\cfrac{\partial x_{d+1}}{\partial z_{d+1}}\cfrac{\partial x_{d+2}}{\partial z_{d+2}}\cdots\cfrac{\partial x_D}{\partial z_D}
det(JG)=∂zd+1∂xd+1∂zd+2∂xd+2⋯∂zD∂xD
根据公式8可以将每一项偏导求出来
d
e
t
(
J
G
)
=
β
d
+
1
β
d
+
2
⋯
β
D
det(J_G)=\beta_{d+1}\beta_{d+2}\cdots\beta_D
det(JG)=βd+1βd+2⋯βD
Coupling Layer Stacking
下面来看Coupling Layer如何叠加假设有多个Coupling Layer如下图
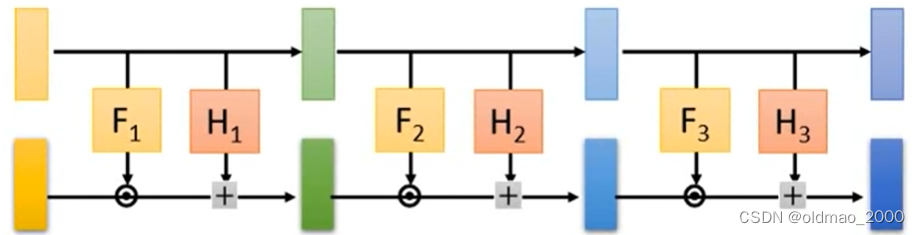
按照单个Coupling Layer的原理我们发现它会把第一层浅黄色部分直接copy到最后一层这样会使得最后的部分和原始输入的noise一样原始输入是从搞屎分布中随机sample出来这样没有啥意义。
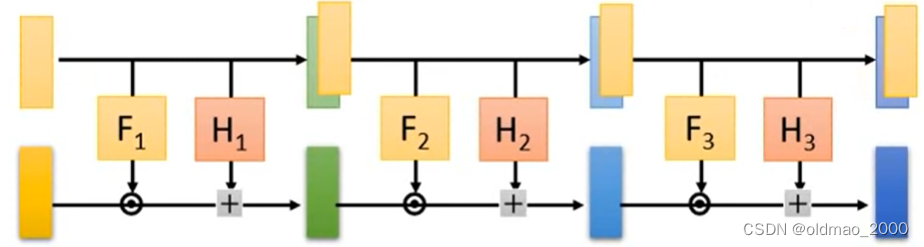
因此在堆叠的时候可以适当做一些反向注意看函数的箭头
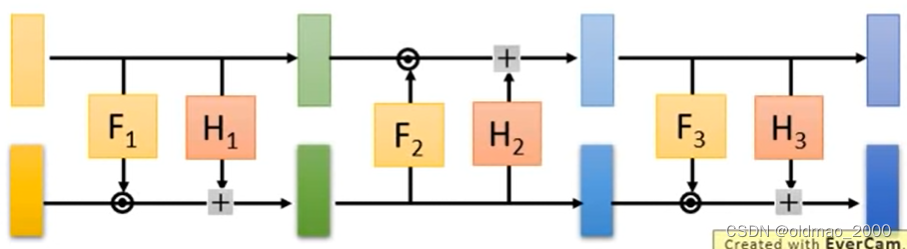
经过Copy操作后变成
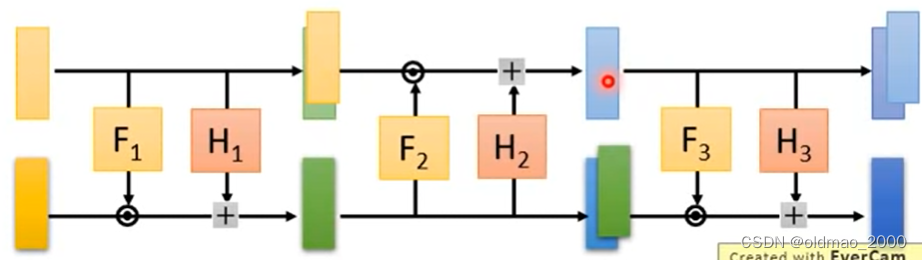
在做图像生成实操的时候如何做反向有两种方法
第一种按棋盘式的前后两两反向

第二种将图片的channel进行反接一层做copy一层做Transform

两种方法还可以混合使用。
1×1 Convolution
另外一个技巧让基于Flow的网络构架对称的技巧就是1×1的卷积这个是15年就提出来的概念但是22年又用在了GLOW上面使得我们在不使用GAN的情况下也能做图像生成。
Glow: Generative Flow with Invertible 1x1 Convolutions
假设输入为
z
z
z输出为
x
x
x由于是图像问题图片中每个像素看做一个单位且有RGB三个channel1×1的卷积过程如下图所示
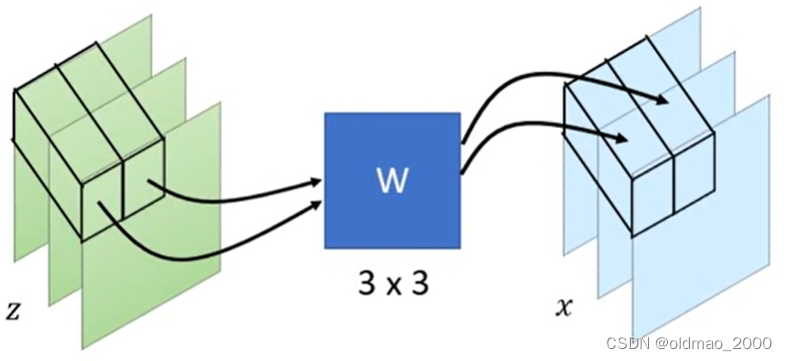
将
z
z
z中的每一个像素对应的3个channel与大小为3×3的矩阵
W
W
W相乘得到x相同位置上的一个像素的3个channel。
x
=
f
(
z
)
=
W
z
(9)
x=f(z)=Wz\tag9
x=f(z)=Wz(9)
矩阵
W
W
W是通过训练学习得来其作用为将3个channel进行shuffle例如
[
0
0
1
1
0
0
0
1
0
]
W
[
1
2
3
]
=
[
3
1
2
]
\overset{W}{\begin{bmatrix} 0& 0&1 \\ 1 & 0&0 \\ 0 & 1 &0 \end{bmatrix}}\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}=\begin{bmatrix} 3 \\ 1 \\ 2 \end{bmatrix}
010001100
W
123
=
312
这样就可以使得在用Coupling Layer stacking的时候不需要进行反接而是让模型自己学习
W
W
W决定如何来交换channel的位置。将
W
W
W加入Generator构架
G
G
G中后也必须是是invertiable的即
W
W
W必须存在
W
−
1
W^{-1}
W−1。GLOW文章中没有证明
W
W
W一定可逆仅提到使用了存在
W
−
1
W^{-1}
W−1的
W
W
W进行初始化并希望在模型自动学习收敛后
W
W
W还是可逆。当然三阶矩阵不可逆的条件比较苛刻除非该矩阵对应的行列式值为0一般三阶矩阵都可以满足可逆这一条件。
下面根据公式9来求单个像素点对应的Jacobian Matrix将该公式写开
[
x
1
x
2
x
3
]
=
[
w
11
w
12
w
13
w
21
w
22
w
23
w
31
w
32
w
33
]
[
z
1
z
2
z
3
]
\begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}=\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} &w_{23} \\ w_{31} &w_{32} &w_{33} \end{bmatrix}\begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix}
x1x2x3
=
w11w21w31w12w22w32w13w23w33
z1z2z3
Jacobian Matrix计算结果就为
j
f
=
[
∂
x
1
/
∂
z
1
∂
x
1
/
∂
z
2
∂
x
1
/
∂
z
3
∂
x
2
/
∂
z
1
∂
x
2
/
∂
z
2
∂
x
2
/
∂
z
3
∂
x
3
/
∂
z
1
∂
x
3
/
∂
z
2
∂
x
3
/
∂
z
3
]
=
[
w
11
w
12
w
13
w
21
w
22
w
23
w
31
w
32
w
33
]
=
W
j_f=\begin{bmatrix} \partial x_1/\partial z_1 & \partial x_1/\partial z_2 & \partial x_1/\partial z_3 \\ \partial x_2/\partial z_1 & \partial x_2/\partial z_2 & \partial x_2/\partial z_3 \\ \partial x_3/\partial z_1 & \partial x_3/\partial z_2 & \partial x_3/\partial z_3 \end{bmatrix}=\begin{bmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} &w_{23} \\ w_{31} &w_{32} &w_{33} \end{bmatrix}=W
jf=
∂x1/∂z1∂x2/∂z1∂x3/∂z1∂x1/∂z2∂x2/∂z2∂x3/∂z2∂x1/∂z3∂x2/∂z3∂x3/∂z3
=
w11w21w31w12w22w32w13w23w33
=W
接下来看整个图片的Jacobian Matrix假设图片大小是
d
×
d
d\times d
d×d
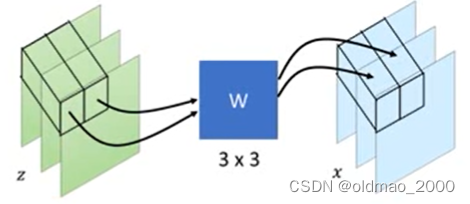
根据上面的图来看只有对应位置上的像素点做了乘
W
W
W的操作而与其他像素点是没有关系的因而整个图片的Jacobian Matrix可以表示为下图
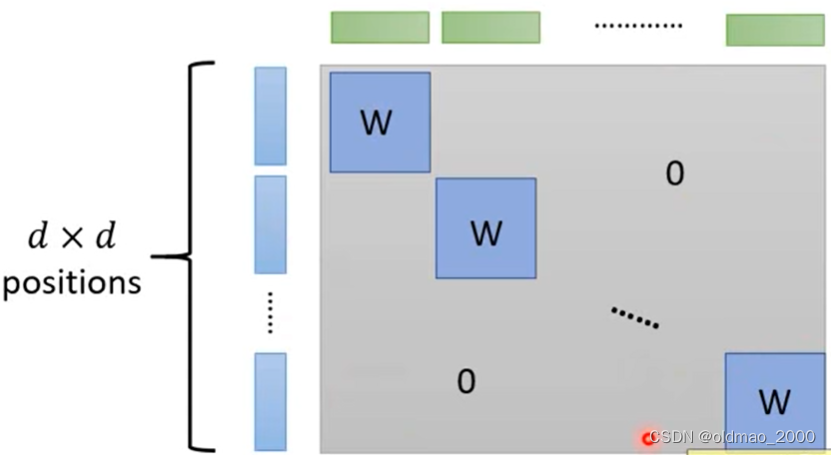
只有对角线部分是由一个个
W
W
W组成其他位置都是0根据线性代数的推论整个矩阵的行列式的值为
(
d
e
t
(
W
)
)
d
×
d
\left(det(W)\right)^{d\times d}
(det(W))d×d
由于
W
W
W是3×3的矩阵其行列式的值很容易算可参加上面有公式。
GLOW效果
接下来演示了OpenAI的GLOW模型效果GLOW模型效果合成
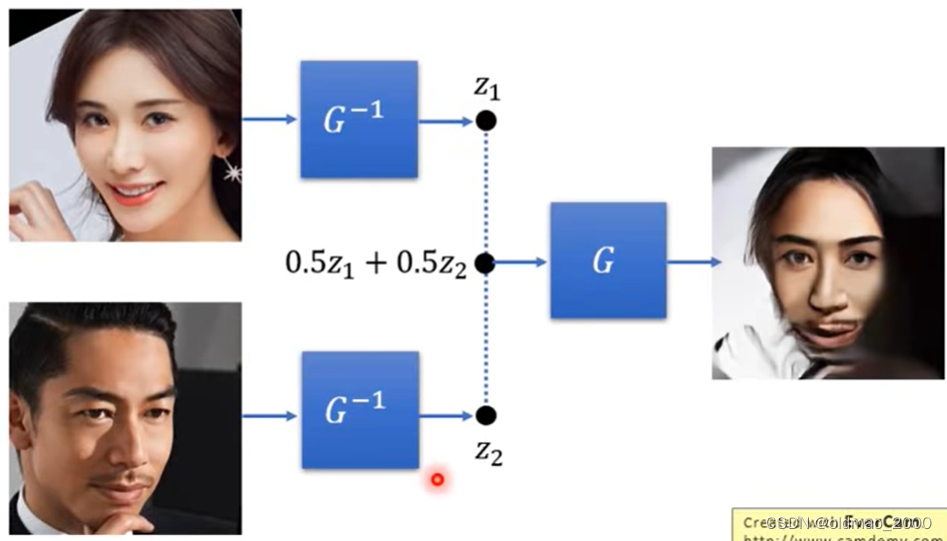
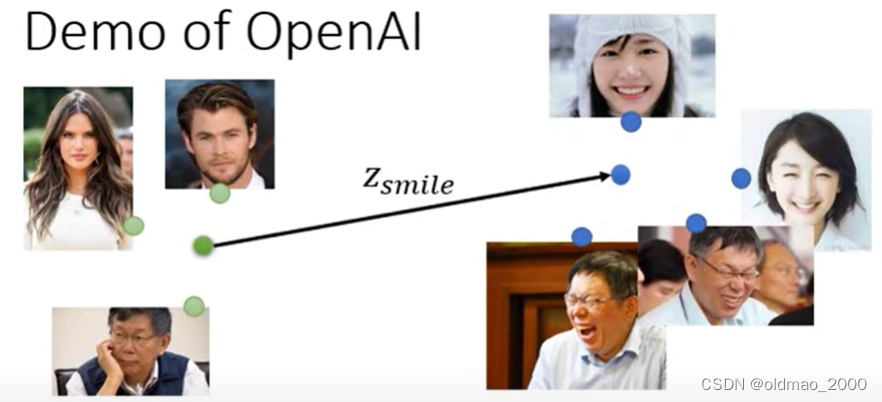
魔改笑脸收集不笑的人脸和有笑容的人脸通过
G
−
1
G^{-1}
G−1求向量后分别求两组人脸的平均然后求差就得到从不笑到笑之间的向量为
z
s
i
m
l
e
z_{simle}
zsimle
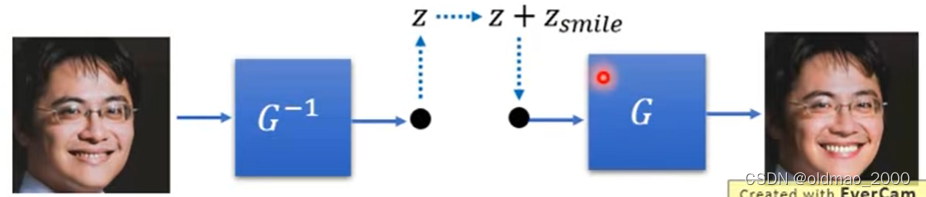
找一张要改笑容的图片通过
G
−
1
G^{-1}
G−1求向量后加上
z
s
i
m
l
e
z_{simle}
zsimle再过
G
G
G得到结果
其他工作
语音合成
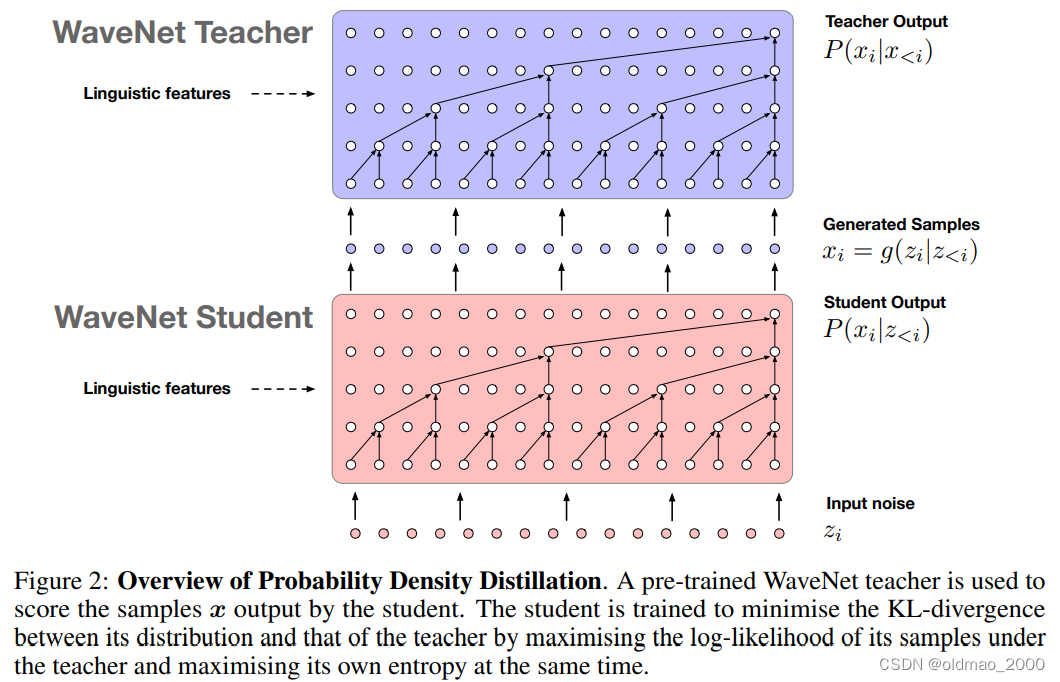
Parallel WaveNet: Fast High-Fidelity Speech Synthesis
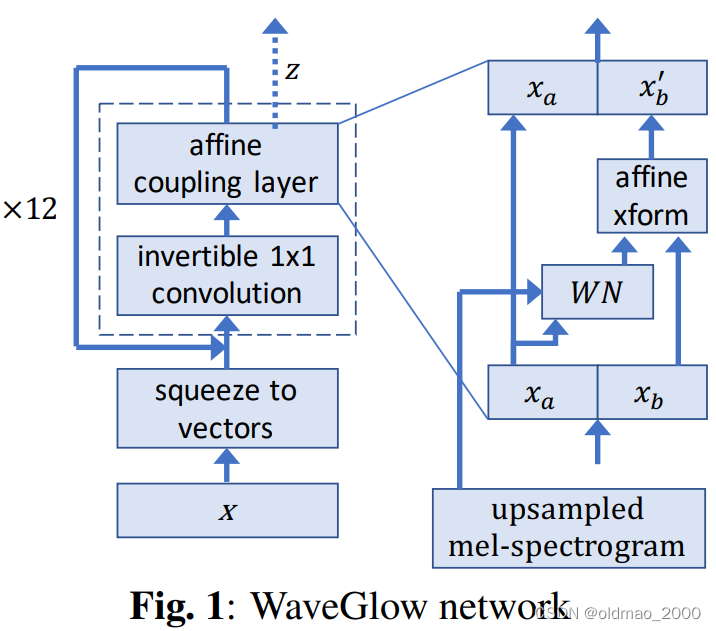
WaveGlow: A Flow-based Generative Network for Speech Synthesis
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

