1 Householder reflector

  Householder反射是这样子的(图片来自瑞典皇家理工学院)

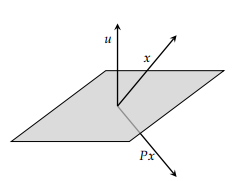
  图中u是长度为1的向量。x是任意向量H是u的Householder reflector。可见无论x是什么向量$Hx$始终除于和u正交的平面上。H和u的关系是
$$H=I-2u{u}^{\ast }$$
  $u^{\ast }$是u的共轭转置$u$是单位向量。在有些书上也写成$u^H$.也就是说H这个矩阵是由$u$确定的。那么接下来的问题是如何精确控制变换方向了。如果能精确控制把向量投影到标准基的方向上那么QR分解就容易了。
  那么这和QR分解有什么关系呢

2 分解步骤

  首先把矩阵A按列向量分块为$(a_1,a_2,\cdots ,a_n)$,设单位矩阵的第一列为$e_1$,取$u$向量为以下向量
$$u=\frac{a_1-\parallel a_1\parallel e_1}{\parallel (a_1-\parallel a_1\parallel e_1)\parallel }$$
  用这个$u$向量构造的Householder矩阵$H$会把$a_1$投影到$e_1$的方向上。也就是
$$H{a}_1=\parallel a_1\parallel e_1$$
  那么$HA$就是这个样子
$$HA=H(a_1,a_2,\cdots ,a_n)=\left(\begin{array}{ccc}\parallel a_1\parallel & \cdots & \ast \\ 0& \cdots & \ast \\ ⋮& \ddots & \ast \\ 0& \cdots & \ast \end{array}\right)$$
  把右边的矩阵叫做B那么有
$$\begin{gathered} HA=B \\ {H}^{-1}HA=H^{-1}B \\ A=H^{-1}B \end{gathered}$$
  Householder变换矩阵是自逆矩阵也是对合矩阵所以$H=H^{-1}$.所以又有
$$A=HB$$
  $B$矩阵的右下角再当成新的子矩阵继续完成这个过程这样得到一系列的H矩阵编号为$H_1,H_2,\cdots ,H_n$.这写矩阵乘以$A$,得到的结果也是不断把对角线以下的元素变成$0$,所以最终结果就是上三角矩阵$R$。但是会发现这些Householder矩阵是不同阶的。为了同阶可以在对角线上补1凑成$n$阶矩阵这种左上角补1的矩阵乘以任何矩阵不会改变左上角的元素。如下面这样处理
$${\tilde{H}}_i={\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & & \ddots & \\ & & & H_i\end{array}\right)}_n$$
  所以整个过程就是
$$\begin{gathered} {\tilde{H}}_n{\tilde{H}}_{n-1}\cdots {\tilde{H}}_2{\tilde{H}}_{1}A=R \\ {\tilde{H}}_1^{-1}{\tilde{H}}_2^{-1}\cdots {\tilde{H}}_{n-1}^{-1}{\tilde{H}}_n^{-1}{\tilde{H}}_n{\tilde{H}}_{n-1}\cdots {\tilde{H}}_2{\tilde{H}}_{1}A={\tilde{H}}_1^{-1}{\tilde{H}}_2^{-1}\cdots {\tilde{H}}_{n-1}^{-1}{\tilde{H}}_n^{-1}R \\ A={\tilde{H}}_1^{-1}{\tilde{H}}_2^{-1}\cdots {\tilde{H}}_{n-1}^{-1}{\tilde{H}}_n^{-1}R \\ A={\tilde{H}}_1{\tilde{H}}_2\cdots {\tilde{H}}_{n-1}{\tilde{H}}_{n}R \end{gathered}$$
  最终这些拼凑为$n$阶的矩阵连乘起来就是Q矩阵最终的结果就是R矩阵。

3 举例

  以这个矩阵为例子
$$\left(\begin{array}{ccc}0& 3& 1\\ 0& 4& -2\\ 2& 1& 2\end{array}\right)$$
  第一次分解得到
$$\left(\begin{array}{ccc}0& 3& 1\\ 0& 4& -2\\ 2& 1& 2\end{array}\right)=\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right)\left(\begin{array}{ccc}2& 1& 2\\ 0& 4& -2\\ 0& 3& 1\end{array}\right)$$
  第二次分解得到
$$\left(\begin{array}{ccc}2& 1& 2\\ 0& 4& -2\\ 0& 3& 1\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 0.8& 0.6\\ 0& 0.6& -0.8\end{array}\right)\left(\begin{array}{ccc}2& 1& 2\\ 0& 5& -1\\ 0& 0& -2\end{array}\right)$$
  第三次分解得到
$$\left(\begin{array}{ccc}2& 1& 2\\ 0& 5& -1\\ 0& 0& -2\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right)\left(\begin{array}{ccc}2& 1& 2\\ 0& 5& -1\\ 0& 0& 2\end{array}\right)$$

4 Python实现

  代码实现如下

    @staticmethod
    def householder_u(x, z, inner_product_matrix=None):
        x_len = vector_len(x, inner_product_matrix)
        xz = mul_num(z, x_len)
        complement = sub(x, xz)
        complement_len = vector_len(complement, inner_product_matrix)
        return mul_num(complement, 1 / complement_len)

    # 获取householder变换的u向量
    def get_householder_u(self, inner_product_matrix=None):
        a1 = self.__vectors[0]
        n = len(a1)
        e1 = [0] * n
        e1[0] = 1
        return Matrix.householder_u(a1, e1, inner_product_matrix)

    # 获取householder矩阵
    def householder_matrix(self, inner_product_matrix=None):
        n = len(self.__vectors)
        unit = Matrix.unit_matrix(n)
        u = self.get_householder_u(inner_product_matrix)
        u_matrix = Matrix([u])
        h = Matrix(unit) - u_matrix * u_matrix.transpose_matrix() * 2
        return h

    # householder变换
    def householder(self, inner_product_matrix=None):
        n = len(self.__vectors)
        r = self
        q = Matrix(Matrix.unit_matrix(n))
        for i in range(n):
            # 子矩阵
            sub_matrix_array = [r.__vectors[j][j:] for j in range(i, n)]
            sub_matrix = Matrix(sub_matrix_array)
            sub_h = sub_matrix.householder_matrix(inner_product_matrix)
            # 左上角补1
            h_array = Matrix.unit_matrix(n)
            for j in range(i, n):
                for k in range(i,n):
                    h_array[j][k] = sub_h.__vectors[j-i][k-i]
            h = Matrix(h_array)
            r = h * r
            print((h * r).to_latex(), '=',h.to_latex(), r.to_latex())
            # sub_r 的内容
            q = q * h
        return q, r