高斯混合模型

  给定变量 $x$ 的有限个观测数据 $x_1,x_2,x_3,\cdots ,x_n$对变量 $x$ 的概率分布 $p(x)$ 进行建模的过程称为对变量 $x$ 的密度估计高斯混合模型Gaussian Mixture ModelGMM是一种得到了广泛使用且非常有效的密度估计方法高斯混合模型是用来表示在总分布中含有 $$K$$ 个高斯分布的概率模型各个高斯分布称为总分布的子分布。混合高斯模型在计算观测数据在总体分布中的概率时不需要观测数据提供关于子分布的信息。

  高斯分布也称正态分布是自然界中广泛存在的一种数据分布形式其概率密度函数公式如 $公式1.1$ 所示

$$N\left(x\mid \mu ,{\sigma }^2\right)=\frac{1}{\sqrt{2{\sigma }^2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\text{\hspace{1em}(1.1)}$$
其中参数 $u$ 表示变量 $x$ 的期望参数 $\sigma$ 表示变量 $x$ 的标准差更一般的情况下当变量是多维数据时即 $\mathbf{x}$ 的维度 $d>1$ 时多元高斯分布的概率密度函数如 $公式1.2$ 所示

$$N(\mathbf{x};\mathbf{\mu },\Sigma )=\frac{1}{\sqrt{(2\pi {)}^d\det (\Sigma )}}\exp \left[-\frac{1}{2}(\mathbf{x}-\mu ){\Sigma }^{-1}(\mathbf{x}-\mu {)}^T\right]\text{\hspace{1em}(1.2)}$$
其中$\mathbf{\mu }$ 是一个 $d$ 维向量代表了 $\mathbf{x}$ 各个维度的的数学期望$\Sigma$ 是一个 $d\times d$ 的矩阵表示了变量 $\mathbf{x}$ 各个维度之间的协方差矩阵。高斯混合模型可以看作 $K$ 个高斯分布的组合其概率分布形式如 $公式1.3$ 所示

$$P(\mathbf{x}\mid \theta )=\sum _{k=1}^K{\alpha }_k\varphi \left(\mathbf{x}\mid {\theta }_k\right)\text{\hspace{1em}(1.3)}$$
其中${\alpha }_k⩾0$ $\sum _{k=1}^K{\alpha }_k=1$ $\mathbf{\theta }=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K,{\theta }_1,{\theta }_2,\dots ,{\theta }_K)$ 表示GMM模型的参数${\mathbf{\theta }}_k$ 表示GMM第 $k$ 个高斯分布的参数当 $\mathbf{x}$ 维度为1时${\mathbf{\theta }}_k=({\mu }_k,{\sigma }_k^2)$ $\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)$ 由公式 $公式1.1$ 给出当 $\mathbf{x}$ 维度大于1时${\mathbf{\theta }}_k=({\mathbf{\mu }}_{\mathbf{k}},{\Sigma }_k)$ $\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)$ 由公式 $公式1.2$ 给出。对于GMM模型的观测数据 ${\mathbf{x}}_i,i=1,2,3\dots ,n$ 可以认为是经过两个采样步骤生成的第一步按照概率 ${\alpha }_k$ 选择第 $k$ 个高斯分布 $\varphi (\mathbf{x}|{\mathbf{\theta }}_k)$ 第二步按照第 $k$ 个高斯分布 $\varphi (\mathbf{x}|{\mathbf{\theta }}_k)$ 采样生成观测数据 ${\mathbf{x}}_i$ 这里需要重点理解的是我们并不知道观测数据 ${\mathbf{x}}_i$ 来自于哪个高斯分布记 ${\omega }_{i,k}\in [1,2,3\dots ,K]$ 表示第 $i$ 个观测数据 ${\mathbf{x}}_i$ 来自第 $k$ 个高斯分布的概率${\omega }_{i,k}$ 是未知的一般将其称为隐变量。下面将介绍利用期望极大算法估计GMM模型参数的思路。

  期望极大Expectation MaximumEM算法是1977年由Dempster等人¹ 总结提出的EM算法是含有隐变量的概率模型参数的极大似然估计法。关于EM算法本身正确性及收敛性的证明可以参考文献² 本文只介绍利用EM算法估计GMM模型参数的简要思路

步骤 1赋予GMM模型参数初值 ${\mathbf{\theta }}^0$ 初值的选择是任意的但需要注意的是EM算法只能收敛到局部最优解所以EM算法对初值是敏感的。

步骤 2利用当前GMM的模型参数为 ${\mathbf{\theta }}^t$求隐变量 ${\omega }_{i,k}$ 的期望。

当 ${\mathbf{\theta }}^t$ 给定时对于 $公式1.3$ 而言 $K$ 个高斯分布 $\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)$ 都是确定的因此可以求出观测数据 ${\mathbf{x}}_i,i=1,2,3\dots ,n$ 属于第 $k$ 个高斯分布的概率如 $公式1.4$ 所示

$${\omega }_{i,k}^t=\frac{{\alpha }_k^t\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)}{\sum _{k=1}^K{\alpha }_k^t\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)}\text{\hspace{1em}(1.4)}$$
步骤 3基于当前的隐变量 ${\omega }_{i,k}$ 的值利用极大似然估计法更新GMM的模型参数为 ${\mathbf{\theta }}^{(t+1)}$ 。

当隐变量 ${\omega }_{i,k}$ 给定时此时估计GMM模型参数就退化为一个不含隐变量的概率模型参数估计问题可以利用极大似然估计法求得当前步骤模型参数的相合估计量如下式所示
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ & \text{当}\;d=… {#eq:Mstep}

为什么高斯模型混合模型GMM理论上可以拟合任意概率密度分布呢

百科搬运工

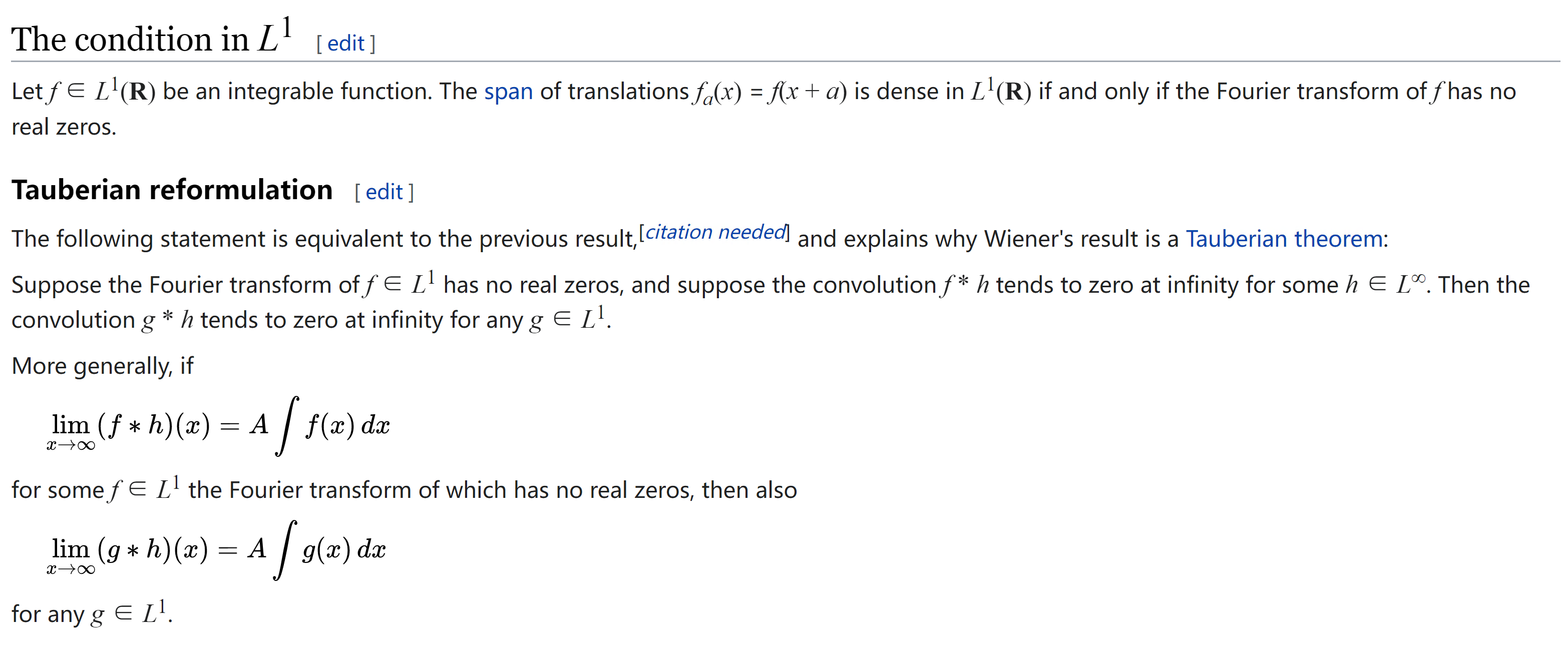
中文说明

  定理实际上比GMM可以逼近任何概率分布条件要强因为只用了平移。另外因为高斯函数的积还是高斯函数似乎用Stone-Weierstrass定理也可以。选用高斯分布的理由其实有很多一方面因为中心极限定理生活中高斯分布非常多另一方面它实在是太好算了。其实第二个理由更充分毕竟对任意的概率分布不可能总是高斯逼近是最好的。不过一般的GMM效果都不错。

你可能需要的参考文献

分别对应百科第一段中引用的两个参考文献

[1] Meir, A., 1963. Tauberian theorems. Israel Journal of Mathematics 1, 29–36. https://doi.org/10.1007/BF02759798
[2] Rudin, W., 1991. Functional analysis, 2nd ed, International Series in Pure and Applied Mathematics. New York : McGraw-Hill.

---

1. Dempster, A.P., Laird, N.M., Rubin, D.B., 1977. Maximum likelihood from incomplete data via the EM algorithm. JOURNAL OF THE ROYAL STATISTICAL SOCIETY, SERIES B 39, 1–38. ↩︎

2. 李航, 《EM算法及其推广》, 收入 统计学习方法, 第2版., 清华大学出版社, 2019, 页 175–183. ↩︎