倍增算法讲解——序列、RMQ和LCA

阿里云国内75折 回扣 微信号：monov8
阿里云国际，腾讯云国际，低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号：monov8 飞机：@monov6

倍增算法

文章目录

定义

倍增 从字面的上意思看就是成倍的增长 ,这是指我们在进行递推时,如果状态空间很大,通常的线性递推无法满足时间和空间复杂度的要求 ,那么我们就可以通过成倍的增长,只递推状态空间中在 2 的整数次幂位置上的值作为代表 。

倍增在序列上的应用

一般分为两个阶段如图。
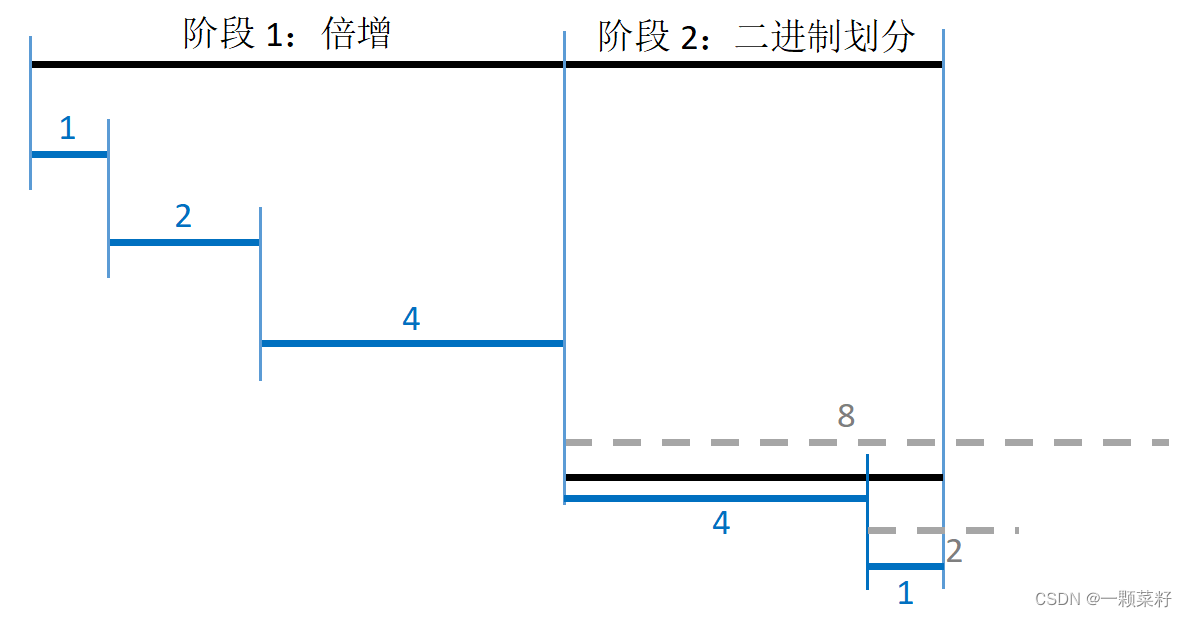
在这里插入图片描述
阶段1倍增找到一个满足条件的边界
阶段2将边界与目标的距离进行二进制划分。

查找

例一

在一个元素递增数组a中查找最大的小于一个数b的数字。
倍增做法设定一个增长长度p和指示当前所指数字的指针k。先尝试a[k + p]是否满足小于b的条件若满足条件则p成2倍增长否则p缩小范围继续尝试直到p缩小到0为止。

def binary_lift(a, b) :
	k, p = 0, 1
	while p : #如果还能扩展k范围则继续扩展
		if k + p - 1 <= len(a) and a[k + p - 1] < b : 
			k += p # 扩展范围
			p <<= 1 #倍增
		else :
			p >>= 1 # 二进制划分
	print(k)

例二

给定长度为 N N N的数列 A A A然后在线询问若干次每次给定一个整数 T T T求出最大的 k k k满足 ∑ i = 1 k A [ i ] ≤ T \sum^k_{i=1}A[i]\le T ∑i=1k​A[i]≤T。

def binary_lift(a, t) :
	length = len(a)
	S = [0] * (length + 1)
	for i in range(1, length + 1) : #前缀和
		S[i] += S[i - 1] + a[i]
	k, p, sum = 0, 1, 0
	while p :
		if k + p <= length and sum + S[k + p] - S[k] <= t : # 倍增
			sum += S[k + p] - S[k]
			k += p
			k >>= 1 # 扩大范围
		else : p <<= 1 #二进制划分

快速幂

求 a 的 b 次方对 p 取模的值。

输入格式
三个整数 a,b,p ,在同一行用空格隔开。

输出格式
输出一个整数表示 a b m o d p a^b mod p abmodp的值。

数据范围
0≤a,b≤109
1≤p≤109
输入样例
3 2 7
输出样例
2

def q_mi(a, b, p) :
	res = 1
	while b :
		if b & 1 :
			res = res * a % p
		b >>= 1 #二进制划分
		a = a * a % p # 倍增
	return res % p
a, b, p = map(int, input().split())
print(q_mi(a, b, p))

RMQ区间最值

RMQ 是 R a n g e M a x i m u m / M i n i m u m Q u e r y Range Maximum/Minimum Query RangeMaximum/MinimumQuery的缩写表示区间最大最小值。使用倍增思想解决 RMQ 问题的方法是 ST 表。

  1. 预处理部分
    一个序列的子区间个数显然有 O ( N 2 ) O(N^2) O(N2)个根据倍增思想我们首先在这个规模为 O ( N 2 ) O(N^2) O(N2)的状态空间中选择一些2的整数次幂的位置作为代表值。
    设f[i, j]表示从i开始长度是 2 j 2^j 2j的区间的最大值。递推边界为f[i, 0] = a[i], 公式 f [ i , j ] = m a x ( f [ i , j − 1 ] , f [ i + 2 j − 1 , j − 1 ] ) f[i, j]= max(f[i, j - 1], f[i + 2^{j - 1}, j - 1]) f[i,j]=max(f[i,j−1],f[i+2j−1,j−1])即长度为 2 j 2^j 2j的子区间的最大值是左右两半长度最大值中较大的一个。
  2. 询问部分
    当询问任意区间 [ l , r ] [l, r] [l,r]的最值时我们先计算一个k使得从l开始的 2 k 2^k 2k个数和以r结尾的 2 k 2^k 2k个数这两段一定覆盖了整个区间[l, r]。这样就能求出最值 m a x ( f [ l , k ] , f [ r − 2 k + 1 , k ) max(f[l, k], f[r - 2^k + 1, k) max(f[l,k],f[r−2k+1,k)。则 2 k < r − l + 1 ≤ 2 ∗ 2 k 2^k <r - l + 1\le 2 * 2^ k 2k<r−l+1≤2∗2k。所以 k = l o g 2 ( r − l + 1 ) k = log_2(r - l + 1) k=log2​(r−l+1)

天才的记忆

从前有个人名叫 WNB他有着天才般的记忆力他珍藏了许多许多的宝藏。

在他离世之后留给后人一个难题专门考验记忆力的啊如果谁能轻松回答出这个问题便可以继承他的宝藏。

题目是这样的给你一大串数字编号为 1 到 N大小可不一定哦在你看过一遍之后它便消失在你面前随后问题就出现了给你 M 个询问每次询问就给你两个数字 A,B要求你瞬间就说出属于 A 到 B 这段区间内的最大数。

一天一位美丽的姐姐从天上飞过看到这个问题感到很有意思主要是据说那个宝藏里面藏着一种美容水喝了可以让这美丽的姐姐更加迷人于是她就竭尽全力想解决这个问题。

但是她每次都以失败告终因为这数字的个数是在太多了

于是她请天才的你帮他解决。如果你帮她解决了这个问题可是会得到很多甜头的哦

输入格式
第一行一个整数 N 表示数字的个数。

接下来一行为 N 个数表示数字序列。

第三行读入一个 M表示你看完那串数后需要被提问的次数。

接下来 M 行每行都有两个整数 A,B。

输出格式
输出共 M 行每行输出一个数表示对一个问题的回答。

数据范围
1≤N≤2×105,
1≤M≤104,
1≤A≤B≤N。

输入样例
6
34 1 8 123 3 2
4
1 2
1 5
3 4
2 3
输出样例
34
123
123
8

from math import log
N, M = 200010, 18
f = [[0] * M for _ in range(N)]
a = [0] * N
# 预处理部分
def init() :
	for i in range(1, n + 1) :
		f[i][0] = a[i]
	k = int(log(n, 2)) + 1
	for length in range(1, k) :
		for l in range(1, n + 1) :
			r = l + (1 << length) - 1
			if r > n : break
			f[l][length] = max(f[l][length - 1], f[l + (1 << (length - 1))][length - 1]) # 倍增
#查询部分		
def query(l, r) :
	k = int(log(r - l + 1, 2))
	return max(f[l][k], f[r - (1 << k) + 1][k])

n = int(input())
a[1 : n + 1] = list(map(int, input().split()))
init()
m = int(input())
for i in range(m) :
	l, r = map(int, input().split())
	print(query(l, r))

LCA最近公共祖先

最近公共祖先简称 LCALowest Common Ancestor。两个节点的最近公共祖先就是这两个点的公共祖先里面离根最远的那个。 为了方便我们记某点集 S = { v 1 , v 2 , … , v n } S=\{v_1,v_2,\ldots,v_n\} S={v1​,v2​,…,vn​} 的最近公共祖先为 LCA ( v 1 , v 2 , … , v n ) \text{LCA}(v_1,v_2,\ldots,v_n) LCA(v1​,v2​,…,vn​)或 LCA ( S ) \text{LCA}(S) LCA(S)。

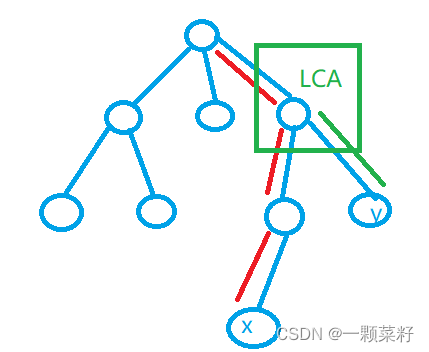
向上标记法

O ( n m ) O(nm) O(nm)

从x向上走到根节点并标记所有经过的节点。
从y向上走到根节点当第一次遇到已标记的节点时就找到LCA(x, y)。
在这里插入图片描述

st = [False] * N
ans = 0

def sign(root, x) :
	if root == x : # 访问节点为x返回True
		st[root] = True
		return True
	i = h[root]
	while ~ i :
		j = e[i]
		if sign(j, x) : # 标记路径上含有x的情况
			st[j] = True
			return True
		i = ne[i]
	return False
falg = True
def dfs(root, y) :
	global ans
	if root == y :
		return True
	i = h[root]
	while ~ i :
		j = e[i]
		if dfs(j) :
			if st[j] and flag:
				ans = j
				flag = False #标记第一次遇见已标记点状态
			return True
		i = ne[i]
	return False
def lca(x, y) :
	sign(root, x)
	dfs(root, y)
	return ans

树上倍增法

在线求LCA O ( n l o g n ) O(nlogn) O(nlogn)

  1. 预处理部分
    设f[x, k]表示 x x x的 2 k 2^k 2k辈祖先即从x向根节点走 2 k 2^k 2k步到达的节点。特别的若该节点不存在则令f[x, k] = 0.f[x, 0]就是x的父节点。除此之外, ∀ k ∈ [ 1 , l o g n ] , f [ x , k ] = [ f [ x , k − 1 ] , k − 1 ] \forall k\in[1, logn], f[x, k] = [f[x, k - 1], k - 1] ∀k∈[1,logn],f[x,k]=[f[x,k−1],k−1]
  2. 查询部分
    基于f数组计算LCA(x, y)分为以下几步
    1. 设d[x]表示x的深度。不妨 d [ x ] ≥ d [ y ] d[x] \ge d[y] d[x]≥d[y](否则可以交换x, y)
    2. 用二进制拆分思想把x向上调整到y同一深度。
    3. 若此时 x = = y x == y x==y说明已经找到了LCALCA 就等于y
    4. 用二进制拆分思想把xy同时向上调整并保持深度一致且二者不会相会。
    5. 此时x,y必定只差一步就相会了它们的父节点就是LCA了。

祖孙询问

给定一棵包含 n 个节点的有根无向树节点编号互不相同但不一定是 1∼n。

有 m 个询问每个询问给出了一对节点的编号 x 和 y询问 x 与 y 的祖孙关系。

输入格式
输入第一行包括一个整数 表示节点个数

接下来 n 行每行一对整数 a 和 b表示 a 和 b 之间有一条无向边。如果 b 是 −1那么 a 就是树的根

第 n+2 行是一个整数 m 表示询问个数

接下来 m 行每行两个不同的正整数 x 和 y表示一个询问。

输出格式
对于每一个询问若 x 是 y 的祖先则输出 1若 y 是 x 的祖先则输出 2否则输出 0。

数据范围
1≤n,m≤4×104,
1≤每个节点的编号≤4×104
输入样例
10
234 -1
12 234
13 234
14 234
15 234
16 234
17 234
18 234
19 234
233 19
5
234 233
233 12
233 13
233 15
233 19
输出样例
1
0
0
0
2

from math import log
from collections import deque

N, M = 40010, 18
h = [-1] * N
e = [0] * N * 2
ne = [-1] * N * 2
idx = 0
f = [[0] * M for _ in range(N)]
d = [0] * N

def add(a, b) :
	global idx
	e[idx] = b
	ne[idx] = h[a]
	h[a] = idx
	idx += 1

def bfs(root) :
	que = deque()
	que.appendleft(root)
	d[root] = 1
	while len(que) :
		t = que.pop()
		i = h[t]
		while ~ i :
			j = e[i]
			if not d[j] : #防止向上遍历
				que.appendleft(j)
				d[j] = d[t] + 1
				f[j][0] = t
				for k in range(1, length) : # 倍增
					f[j][k] = f[f[j][k - 1]][k - 1]
			i = ne[i] 
def lca(a, b) :
	if d[a] < d[b] : a, b = b, a
	for i in range(length, -1, -1) : # 二进制拆分
		if d[f[a][i]] >= d[b] : # 尝试跳跃i距离最终必定跳到与b同一高度
			a = f[a][i]
	if a == b : return b
	for i in range(length, -1, -1) : # 二进制拆分
		if f[a][i] != f[b][i] : # 尝试跳跃如果没跳跃到公共祖先节点否则缩小区间再跳。
			a, b = f[a][i], f[b][i]
	return f[a][0]

n = int(input())
length = int(log(n, 2)) + 1
root = 0
for i in range(n) :
	a, b = map(int, input().split())
	if ~ b :
		add(a, b), add(b, a)
	else : root = a

bfs(root)

m = int(input())
for i in range(m) :
	a, b = map(int, input().split())
	p = lca(a, b)
	if p == a : print(1)
	elif p == b : print(2)
	else : print(0)

Tarjan算法

离线求LCA O ( n + m ) O(n + m) O(n+m)

Tarjan算法本质是使用并查集对“向上标记法”的优化。
在深度优先遍历的任意时刻树中节点分为3类

  1. 已经访问完毕并且回溯的节点。在这些节点标记一个整数2.
  2. 已经开始递归但尚未回溯的节点。这些节点就是当前正在访问的节点x以及x的祖先。在这些节点上标记一个整数1.
  3. 尚未访问的节点。这些节点没有标记。

对于正在访问的节点 x x x它到根节点的路径已经标记为1.若y是已经访问完毕并且回溯的节点则LCA(x, y)就是从y向上走到根第一个遇到标记为1的节点。
可以利用并查集进行优化当一个节点获得整数2的标记时把它所在的集合合并到它父节点所在的集合中合并时它的父节点的标记一定为1且单独构成一个集合。
这相当于每个完成回溯的节点都有一个指针指向它的父节点只需要查询y所在集合代表元素就等价于y一直向上一直走到一个开始递归但尚未回溯的节点(标记1)即LCA(x, y)

距离

给出 n 个点的一棵树多次询问两点之间的最短距离。

注意

边是无向的。
所有节点的编号是 1,2,…,n。
输入格式
第一行为两个整数 n 和 m。n 表示点数m 表示询问次数

下来 n−1 行每行三个整数 x,y,k表示点 x 和点 y 之间存在一条边长度为 k

再接下来 m 行每行两个整数 x,y表示询问点 x 到点 y 的最短距离。

树中结点编号从 1 到 n。

输出格式
共 m 行对于每次询问输出一行询问结果。

数据范围
2≤n≤104,
1≤m≤2×104,
0<k≤100,
1≤x,y≤n
输入样例1
2 2
1 2 100
1 2
2 1
输出样例1
100
100
输入样例2
3 2
1 2 10
3 1 15
1 2
3 2
输出样例2
10
25

N = 10010
M = N * 2

h = [-1] * N
e = [0] * M
w = [0] * M
ne = [-1] * M
idx = 0
dist = [0] * N
res = [0] * M
st = [0] * N
p = [0] * N
query = [[] for _ in range(N)]

def add(a, b, c) :
    global idx
    e[idx] = b
    w[idx] = c
    ne[idx] = h[a]
    h[a] = idx
    idx += 1
def find(x) :
	if x != p[x] : p[x] = find(p[x])
	return p[x]

def dfs(u, fa) : #求每个节点到根节点距离
	i = h[u]
	while ~ i :
		j = e[i]
		if j != fa : #防止回父节点
			dist[j] = dist[u] + w[i]
			dfs(j, u)
		i = ne[i]
def tarjan(u) :
	st[u] = 1
	i = h[u]
	while ~ i :
		j = e[i]
		if not st[j] : # 防止多次遍历
			tarjan(j)
			p[j] = u # 回溯完合并到此时为1的节点的集合
		i = ne[i]
	for item in query[u] :
		y, id = item[0], item[1]
		anc = find(y)
		if st[y] == 2 :
			res[id] = dist[u] + dist[y] - dist[anc] * 2
	st[u] = 2 #标记回溯

n, m = map(int, input().split())

for i in range(n - 1) :
    a, b, c = map(int, input().split())
    add(a, b, c), add(b, a, c)
    
for i in range(1, n + 1) : #初始化并查集
    p[i] = i

for i in range(m) :
    a, b = map(int, input().split())
    if a != b :
        query[a].append([b, i])
        query[b].append([a, i])

dfs(1, -1)    
tarjan(1)

for i in range(m) :
    print(res[i])

总结

其实很多二进制优化的题目都可以归结为倍增和二进制拆分多重背包就是个例子。

阿里云国内75折 回扣 微信号：monov8
阿里云国际，腾讯云国际，低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号：monov8 飞机：@monov6
返回列表

上一篇：vtkPolyData数据的空间变换

下一篇：Unity学习笔记--如何在Unity运行cmd？并且在Unity中利用cmd操作svn（例如生成svn--diff文件）

“倍增算法讲解——序列、RMQ和LCA” 的相关文章

二叉树试题（Python实现）1年前 (2023-02-02)
相比传统专线网络，爱快、飞连等主流SD-WAN方案好在哪里？1年前 (2023-02-02)
195136-58-4，2‘,7‘-Difluorofluorescein，2，7-二氟荧光素1年前 (2023-02-02)
非dbca静默安装~字符集设定1年前 (2023-02-02)
SpringBoot 项目中配置多个 Jackson 的 ObjectMapper ，以及配置遇到的坑1年前 (2023-02-02)
获取某地模型并用Cesium加载(一)1年前 (2023-02-02)
深入学习IO多路复用 select/poll/epoll 实现原理1年前 (2023-02-02)
Codeforces 1630 E Making It Bipartite 题解 (Dilworth定理)1年前 (2023-02-02)
浅谈一下go语言中的slice及其一些小坑1年前 (2023-02-02)
测试工程师正遭「革命」 AI将改写测试模式1年前 (2023-02-02)

阿里云国际版