施密特正交化(Gram-Schmidt Orthogonalization)

注本博文为本人阅读论文、文章后的原创笔记未经授权不允许任何转载或商用行为否则一经发现本人保留追责权利。有问题可留言联系欢迎指摘批评共同进步

1 Gram-Schmidt的计算公式推导

问 以三维情况为例已知三个线性无关的向量$\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$如何能找到三个正交向量${\mathbf{\alpha }}_1$、${\mathbf{\alpha }}_2$、${\mathbf{\alpha }}_3$在归一化后能形成标准正交基${\mathbf{e}}_1$、${\mathbf{e}}_2$、${\mathbf{e}}_3$ ?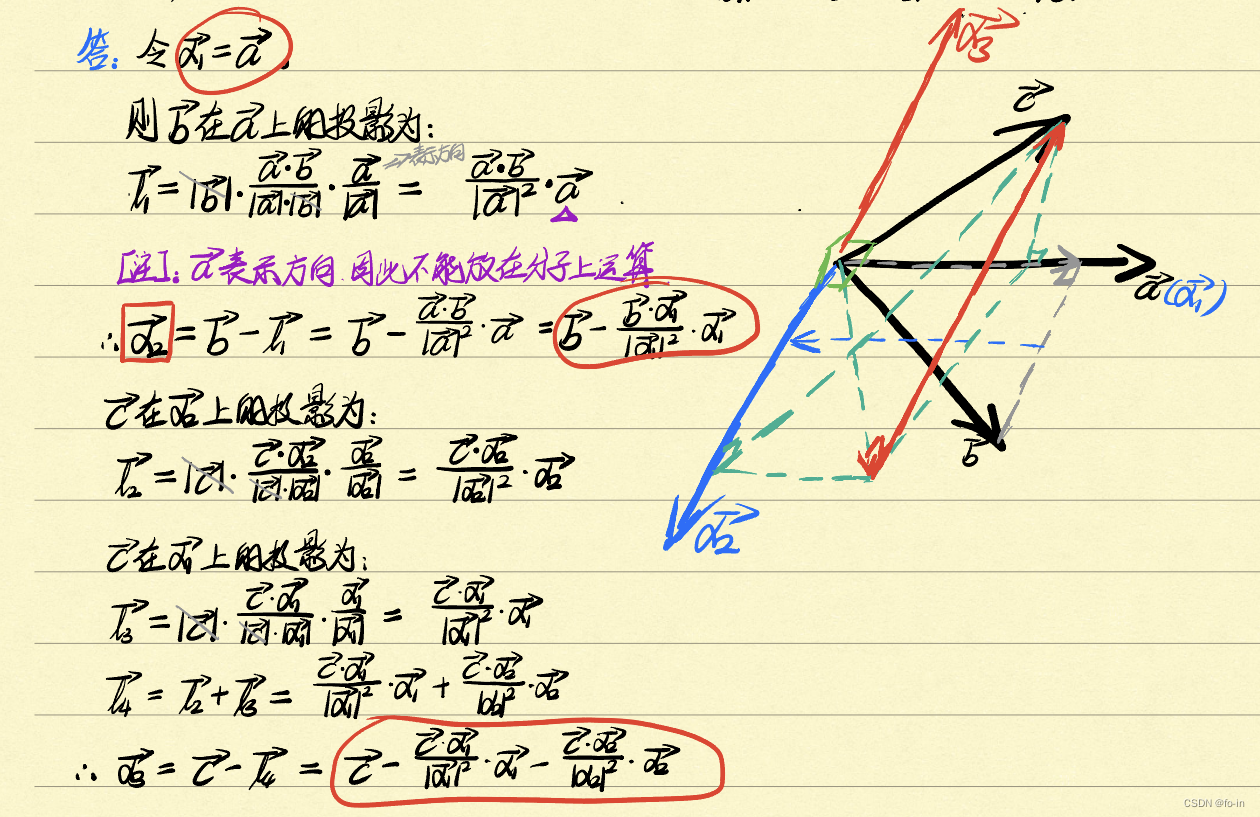

公式:

• 对三个线性无关的向量$\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$进行Gram-Schmidt正交化所得的正交向量${\mathbf{\alpha }}_1$、${\mathbf{\alpha }}_2$、${\mathbf{\alpha }}_3$分别为:
  $$\begin{array}{rl}{\mathbf{\alpha }}_1& =\mathbf{a}\\ {\mathbf{\alpha }}_2& =\mathbf{b}-\frac{\mathbf{b}{\mathbf{\alpha }}_1}{|{\mathbf{\alpha }}_1{|}^2}{\mathbf{\alpha }}_1\\ {\mathbf{\alpha }}_3& =\mathbf{c}-\frac{\mathbf{c}{\mathbf{\alpha }}_1}{|{\mathbf{\alpha }}_1{|}^2}{\mathbf{\alpha }}_1-\frac{\mathbf{c}{\mathbf{\alpha }}_2}{|{\mathbf{\alpha }}_2{|}^2}{\mathbf{\alpha }}_2\end{array}$$
• 对$n$个线性无关的向量$\mathbf{a}$、$\mathbf{b}$、$\cdots$、$\mathbf{x}$进行Gram-Schmidt正交化所得的正交向量${\mathbf{\alpha }}_1$、${\mathbf{\alpha }}_2$、$\cdots$、${\mathbf{\alpha }}_{\mathbf{n}}$分别为:
  $$\begin{array}{rl}{\mathbf{\alpha }}_1& =\mathbf{a}\\ {\mathbf{\alpha }}_2& =\mathbf{b}-\frac{\mathbf{b}{\mathbf{\alpha }}_1}{|{\mathbf{\alpha }}_1{|}^2}{\mathbf{\alpha }}_1\\ {\mathbf{\alpha }}_3& =\mathbf{c}-\frac{\mathbf{c}{\mathbf{\alpha }}_1}{|{\mathbf{\alpha }}_1{|}^2}{\mathbf{\alpha }}_1-\frac{\mathbf{c}{\mathbf{\alpha }}_2}{|{\mathbf{\alpha }}_2{|}^2}{\mathbf{\alpha }}_2\\ ⋮& \\ {\mathbf{\alpha }}_{\mathbf{n}}& =\mathbf{x}-\frac{\mathbf{x}{\mathbf{\alpha }}_1}{|{\mathbf{\alpha }}_1{|}^2}{\mathbf{\alpha }}_1-\frac{\mathbf{x}{\mathbf{\alpha }}_2}{|{\mathbf{\alpha }}_2{|}^2}{\mathbf{\alpha }}_2-\cdots -\frac{\mathbf{x}{\mathbf{\alpha }}_{\mathbf{n}-1}}{|{\mathbf{\alpha }}_{\mathbf{n}-1}{|}^2}{\mathbf{\alpha }}_{\mathbf{n}-1}\end{array}$$
  公式解读在使用第n个向量计算第n个正交向量时只要在第n个向量中排除掉前(n-1)个正交向量的组分就能得到第n个正交向量。

具体推导的图解请参看知乎回答。

2 Gram-Schmidt的意义

将非正交基转为正交基便于表示。
通俗来说就是将一对歪歪斜斜的基向量掰成标准正交基。强迫症

3 Modified Gram-Schmidt (以算法模式计算正交向量)

Gram-Schmidt公式推到中的方法是纯数的方法但是在数值运算方法中计算机操作不会严格按照数学方法来。具体如下所述。

• 从Gram-Schmidt分解结果可以看出
  若对线性无关向量组{${\mathbf{w}}_{\mathbf{k}}$}进行Schmidt正交化得到标准正交基{${\mathbf{u}}_{\mathbf{k}}$}经过移项可得到原向量组 可以表示为标准正交基的线性组合
  $$\begin{array}{rl}{\mathbf{w}}_1& =r_{11}{\mathbf{u}}_1\\ {\mathbf{w}}_2& =r_{21}{\mathbf{u}}_1+r_{22}{\mathbf{u}}_2\\ & ⋮\\ {\mathbf{w}}_{\mathbf{L}}& =r_{L1}{\mathbf{u}}_1+r_{L2}{\mathbf{u}}_2+\cdots +r_{LL}{\mathbf{u}}_{\mathbf{L}}\end{array}$$
  因此要完成正交化分解我们需要找系数组{$r_k$}和标准正交基{${\mathbf{u}}_{\mathbf{k}}$}
  

由此我们看拿出Modified G-S的思想是
使用第k个线性无关向量组的向量${\mathbf{w}}_{\mathbf{k}}$计算第k个正交基${\mathbf{u}}_{\mathbf{k}}$时就是在${\mathbf{w}}_{\mathbf{k}}$中排除掉前$k-1$个正交基的组分剩余的就是${\mathbf{u}}_{\mathbf{k}}$的组分再除以系数即可。

3.1 Modified G-S会出现的问题当矩阵开始存在微小误差时会在运算过程中不断累积误差导致越算越不准确以至于计算所得的基不正交

• 情景假设$e$是一个接近与0的正数作为一个微小的初始误差那么请对矩阵$$\mathbf{W}=\left(\begin{array}{ccc}1& 1& 1\\ e& 0& 0\\ 0& e& 0\\ 0& 0& e\end{array}\right)$$ 进行Gram-Schmidt正交化
  
  此时问题就很明显地体现出来了向量${\mathbf{u}}_2$和${\mathbf{u}}_3$明显不正交没法作为正交基使用。
  问题的原因误差“e”作为一个很小的误差在每一次派出组分操作的过程中都被积累起来了误差积累导致越往后算越不准确Gram-Schmidt就失效了。

为了解决这一问题就有了Stable Gram-Schmidt算法SGS。

4 Stable Gram-Schmidt

不同于Modified Gram-SchmidtSGS算法的核心思想是
每使用一个线性无关组向量${\mathbf{w}}_{\mathbf{k}}$求出一个单位正交基向量${\mathbf{u}}_{\mathbf{k}}$那么剩余的${\mathbf{w}}_{\mathbf{k}+1}$到${\mathbf{w}}_{\mathbf{L}}$这些向量都要立即原地减去其中所含的${\mathbf{u}}_{\mathbf{k}}$组分进行更新。

每计算出一个新的单位正交基向量就当场把剩余线性无关组向量中的此组分排除掉

4.1 G-S 的复杂度计算量

4.2 使用SGS算法解决误差问题

与3.1中的问题一致使用SGS可以抵消微小误差的影响算法更具有鲁棒性。

4.3 MGS和SGS运算的区别在哪里

我们注意到使用两种算法计算所得的${\mathbf{u}}_3$向量时不同的因此着重比较一下两算法计算${\mathbf{u}}_3$时的差别(${\mathbf{u}}_3=\frac{{\mathbf{v}}_3}{||{\mathbf{v}}_3|{|}_2}$)

1. MGS:当使用到${\mathbf{w}}_3$计算${\mathbf{u}}_3$时从${\mathbf{w}}_3$中一次性减去${\mathbf{u}}_1$和${\mathbf{u}}_2$的组分
   $${\mathbf{v}}_3={\mathbf{w}}_3-({\mathbf{u}}_1^{\mathbf{T}}{\mathbf{w}}_3){\mathbf{u}}_1-({\mathbf{u}}_2^{\mathbf{T}}{\mathbf{w}}_3){\mathbf{u}}_2$$
2. SGS当利用${\mathbf{w}}_1$求出${\mathbf{u}}_1$时${\mathbf{w}}_2$和${\mathbf{w}}_3$都立即减去其中所含的${\mathbf{u}}_1$组分进行更新当利用${\mathbf{w}}_2^{\mathbf{new}}$求出${\mathbf{u}}_2$时${\mathbf{w}}_3^{\mathbf{new}}$立即减去其中所含的${\mathbf{u}}_2$组分进行更新然后再求出${\mathbf{u}}_3$
   $$\begin{array}{rl}{\mathbf{w}}_3^{\mathbf{new}}& ={\mathbf{w}}_3-({\mathbf{u}}_1^{\mathbf{T}}{\mathbf{w}}_3){\mathbf{u}}_1\\ {\mathbf{v}}_3& ={\mathbf{w}}_3^{\mathbf{new}}-({\mathbf{u}}_2^{\mathbf{T}}{\mathbf{w}}_3^{\mathbf{new}}){\mathbf{u}}_2\\ & =({\mathbf{w}}_3-({\mathbf{u}}_1^{\mathbf{T}}{\mathbf{w}}_3){\mathbf{u}}_1)-({\mathbf{u}}_2^{\mathbf{T}}({\mathbf{w}}_3-({\mathbf{u}}_1^{\mathbf{T}}{\mathbf{w}}_3){\mathbf{u}}_1)){\mathbf{u}}_2\\ & ={\mathbf{w}}_3-({\mathbf{u}}_1^{\mathbf{T}}{\mathbf{w}}_3){\mathbf{u}}_1-({\mathbf{u}}_2^{\mathbf{T}}{\mathbf{w}}_3){\mathbf{u}}_2+({\mathbf{u}}_1^{\mathbf{T}}{\mathbf{w}}_3)({\mathbf{u}}_2^{\mathbf{T}}{\mathbf{u}}_1){\mathbf{u}}_2\end{array}$$
   由此可见SGS相较于MGS只是多了最后一项$({\mathbf{u}}_1^{\mathbf{T}}{\mathbf{w}}_3)({\mathbf{u}}_2^{\mathbf{T}}{\mathbf{u}}_1){\mathbf{u}}_2$.

从理论上讲${\mathbf{u}}_1$与${\mathbf{u}}_2$是要正交的因此${\mathbf{u}}_2^{\mathbf{T}}{\mathbf{u}}_1=0$最后多出的这一项在理论上就是不存在了。
但是在数值计算(计算机运算)时候存在一定的误差此时最后这一项不再为0它的存在也有助于保证在误差存在情况下的稳定性。
这一项在理论上不存在但实际上有利于保持stability.

5 GS和LS最小二乘法

在一个$k$维空间中我们已知了$k-1$个单位正交基向量${\mathbf{u}}_1$、${\mathbf{u}}_2$、$\cdots$、${\mathbf{u}}_{\mathbf{k}-1}$这些正交基列向量组成一个矩阵$\mathbf{A}$={${\mathbf{u}}_1{\mathbf{u}}_2\cdots {\mathbf{u}}_{\mathbf{k}-1}$}。此外还已知一个在$k$维上都有分量的向量$\mathbf{w}$。问如何找到第$k$个单位正交基向量${\mathbf{u}}_{\mathbf{k}}$呢

实际上要找到这最后一个正交向量我们只需要排除掉向量$\mathbf{w}$中所含有的前($k-1$)个单位正交向量组分即可。因此我们可以找一个系数向量$\mathbf{x}$其中包含了前($k-1$)个单位正交向量组分的系数在所有可能的向量$\mathbf{x}$中我们希望$\mathbf{Ax}$就是向量$\mathbf{w}$中前($k-1$)个单位正交向量组分因此可以使用LS算法来进行优化
$$\begin{gathered} {\mathbf{x}}^{\ast }=arg\underset{x}{\min }||\mathbf{w}-\mathbf{Ax}|{|}_2^2 \\ {\mathbf{v}}_{\mathbf{k}}=\mathbf{w}-\mathbf{A}{\mathbf{x}}^{\ast } \\ {\mathbf{u}}_{\mathbf{k}}=\frac{{\mathbf{v}}_{\mathbf{k}}}{||{\mathbf{v}}_{\mathbf{k}}|{|}_2} \end{gathered}$$
我们来看看这个最优的${\mathbf{x}}^{\ast }$究竟是什么呢
$$\begin{array}{rl}{\mathbf{x}}^{\ast }& =arg\underset{x}{\min }||\mathbf{w}-\mathbf{Ax}|{|}_2^2\\ & =({\mathbf{A}}^{\mathbf{T}}\mathbf{A}){\mathbf{A}}^{\mathbf{T}}{\mathbf{w}}_{\mathbf{k}}\\ & ={\mathbf{A}}^{\mathbf{T}}{\mathbf{w}}_{\mathbf{k}}\\ & =\left(\begin{array}{c}{\mathbf{u}}_1^{\mathbf{T}}{\mathbf{w}}_{\mathbf{k}}\\ ⋮\\ {\mathbf{u}}_{\mathbf{k}-1}^{\mathbf{T}}{\mathbf{w}}_{\mathbf{k}}\end{array}\right)\end{array}$$
果然最优的${\mathbf{x}}^{\ast }$就是由向量$\mathbf{w}$中前$k-1$个单位正交基的组分的系数组成的。这样才能实现$||\mathbf{w}-\mathbf{Ax}|{|}_2^2$的最小化即当向量$\mathbf{w}$排除到其他组分后剩下的${\mathbf{u}}_{\mathbf{k}}$组分才能恰好与矩阵$\mathbf{A}$所确定的超平面正交。
所以回到问题最后一个正交向量是
$${\mathbf{v}}_{\mathbf{k}}=\mathbf{w}-\mathbf{A}{\mathbf{x}}^{\ast }(把组分全部排除掉)$$

6 参考资料

• 讲解视频数值线性代数之QR分解 P3~P5
• 知乎回答