吴恩达《机器学习》——PCA降维

数据集、源文件可以在Github项目中获得
链接: https://github.com/Raymond-Yang-2001/AndrewNg-Machine-Learing-Homework

1. 主成分分析

1.1 数据降维动机

在某些情况下机器学习使用的数据可能十分巨大这种情况下对数据进行压缩就显得十分必要。假设某一数据集包括两个特征维度圆形的半径和圆形的面积。根据简单的数学知识这两个特征实际上是互相关联的从描述圆特征的角度来说半径和面积并没有什么不同在机器学习中完全可以只是用一个特征进行学习。

这就是数据降维使得数据中某些“冗余”的特征维度被压缩从而得到更低位的数据表示——当然这种压缩是建立在尽可能减小数据信息的损失上的。

1.2 PCA降维目标问题分析

假设我们有如下数据

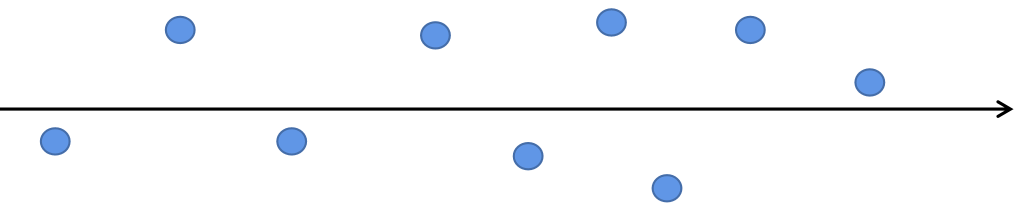
如果要对数据进行维度压缩从二维变成一位显然水平方向是更适合作为压缩后的维度的。从数学角度来看是因为水平方向的方差要大于垂直方向也就意味着水平方向的特征相对于垂直方向来说具有更大的特征空间有更丰富的特征的值的选则也就是对样本更有区分度。

所以PCA的优化目标可以总结为如下两个

1. 降维后同一维度的方差最大
2. 不同维度间的相关度为0

如果不同维度的特征间存在相关度则证明这两个特征间存在某种内在的关联从一个特征能推理出另一个特征显然这没有达到降维的最好目标。

2. PCA数学原理分析

为了同时表示同一维度间的方差和不同维度间的相关性我们引入了协方差矩阵。设数据维度为$D$则协方差矩阵为
$$C={\left[\begin{array}{cccc}cov(x_1,x_1)& cov(x_1,x_2)& \cdots & cov(x_1,x_D)\\ ⋮& ⋮& \ddots & ⋮\\ cov(x_D,x_1)& cov(x_D,x_2)& \cdots & cov(x_D,x_D)\end{array}\right]}_{D\times D}$$
对角线上的元素表明了同一维度的方差不同维度间的方差表明了不同维度间的相关性。优化后的理想矩阵为
$$C^{\prime }={\left[\begin{array}{cccc}{\delta }_{11}& 0& \cdots & 0\\ 0& {\delta }_{22}& \cdots & 0\\ 0& 0& \ddots & ⋮\\ 0& 0& \cdots & {\delta }_{RR}\end{array}\right]}_{R\times R}$$
并且$X$为原数据矩阵形状为$(N,D)$$P$为降维变换矩阵。

考虑协方差矩阵的计算
$$C^{\prime }=\frac{1}{N}(XP{)}^{\top }(XP)=\frac{1}{N}{P}^{\top }{X}^{\top }XP=P^{\top }\left(\frac{1}{N}{X}^{\top }X\right)P=P^{\top }CP$$
要尽量减少不同维度间的相关度设$P^{\top }P=I$即$P$的列是正交的。

优化问题如下
$$\{\begin{array}{rl}& \max \mathrm{tr}({\mathrm{P}}^{\top }\mathrm{CP})\\ & P^{\top }P=I\end{array}$$

采用拉格朗日算子得到无条件的极值问题
$$f(P)=\mathrm{tr}({\mathrm{P}}^{\top }\mathrm{CP})+\lambda (\mathrm{I}-{\mathrm{P}}^{\top }\mathrm{P})$$
对$f(P)$求导
$$\frac{\partial tr(P^{\top }CP)}{\partial P}=\frac{\partial tr(P{P}^{\top }C)}{\partial P}=(P^{\top }C{)}^{\top }=C^{\top }P$$
$$\frac{\partial \lambda (I-P^{\top }P)}{\partial P}=-\lambda P$$
这里用到了迹和矩阵导数的求导的一些知识不理解得到话可以自行查阅一些线性代数的知识。
$$\frac{\partial f(P)}{\partial P}=C^{\top }P+\lambda P$$
由于$C$是对阵矩阵所以
$$\frac{\partial f(P)}{\partial P}=CP-\lambda P$$
$$\frac{\partial f(P)}{\partial P}=0\Rightarrow CP=\lambda P$$
到这里就可以看出$P$实际上是$C$的特征向量矩阵。事实上对称矩阵特征值不等的特征向量是正交的。

另外有
$$P^{\top }CP=P^{\top }\lambda P$$
由于特征值矩阵$\lambda$是一个对角矩阵除了对角线均为0所以$C=P^{\top }\lambda P=\lambda P^{\top }P=\lambda$

可以发现$\lambda$实际上就代表了各个维度的方差也就是说特征值=方差。选择大方差的维度保留就是保留特征值较大的维度。

2.1 求协方差矩阵的碎碎念

先前我们提到求对一个$(n\_sample=N,n\_feature=D)$的矩阵$X$求协方差矩阵公式如下
$$C=\frac{1}{N}{X}^{\top }X$$
接下来将进行理论推导为什么协方差要这么求

从概率论的知识可知两个随机变量$X,Y$的协方差如下
$$cov(X,Y)=\mathbb{E}[(X-{\mu }_X)(Y-{\mu }_Y)]$$
其中${\mu }_X,{\mu }_Y$分别是两个随机变量的均值。

我们在对数据进行PCA之前先要对数据进行规范化使得其均值为0通常采用方法是减去均值即$X_{new}=X-{\mu }_X$这样在计算协方差的时候我们可以得到
$$cov(X,Y)=\mathbb{E}(XY)$$
这里$X,Y$都是数据的某一维度。转换成矩阵运算我们可以得到
$$Cov=\frac{1}{N}{X}^{\top }X$$

当然我们如果考虑对样本进行无偏估计在求期望的时候均值会改写为$\mathbb{E}(\mathbb{X})=\frac{1}{N-1}{\sum }_{i=1}^N{X}_i$不熟悉的话可以回顾一下概率论的相关知识这样我们得到的协方差矩阵是
$$Cov=\frac{1}{N-1}{X}^{\top }X$$
在numpy库中采用的计算方法就是这种。

2.2 PCA实现方法

由上文可知实现PCA的步骤如下

1. 对输入求协方差矩阵$C$
2. 求矩阵$C$的特征值和特征向量按照特征值降序排序
3. 保留k个维度选取前k个特征向量组成矩阵$P$
4. 新的数据矩阵为$C^{\prime }=XP$

3. Python实现

import numpy as np


class PCA:
    """
    ----------------------------------------------------------------------------
    Attributes:
    components_: ndarray with shape of (n_features, n_components)
        Principal axes in feature space, representing the directions of maximum
        variance in the data.

    explained_variance_ : ndarray of shape (n_components,)
        The amount of variance explained by each of the selected components.

    explained_variance_ratio_ : ndarray of shape (n_components,)
        Percentage of variance explained by each of the selected components.
    """
    def __init__(self, n_components):
        self.n_components = n_components
        self.explained_variance_ = None
        self.explained_variance_ratio_ = None
        self.components_ = None

        self.__mean = None

    def fit(self, x):
        """
        :param x: (n,d)
        :return:
        """
        self.__mean = x.mean(axis=0)
        x_norm = x - self.__mean
        x_cov = (x_norm.T @ x_norm) / (x.shape[0] - 1)
        vectors, variance, _ = np.linalg.svd(x_cov)
        # (n_feature, n_components)
        self.components_ = vectors[:, :self.n_components]
        if len(self.components_.shape) == 1:
            self.components_ = np.expand_dims(vectors[:, :self.n_components], axis=1)
        self.explained_variance_ = variance[:self.n_components]
        self.explained_variance_ratio_ = self.explained_variance_ / variance.sum()

    def transform(self, x):
        """
        :param x: (n, n_feature)
        :return:
        """
        if self.__mean is not None:
            x = x - self.__mean
        x_transformed = x @ self.components_
        return x_transformed

数据集可视化

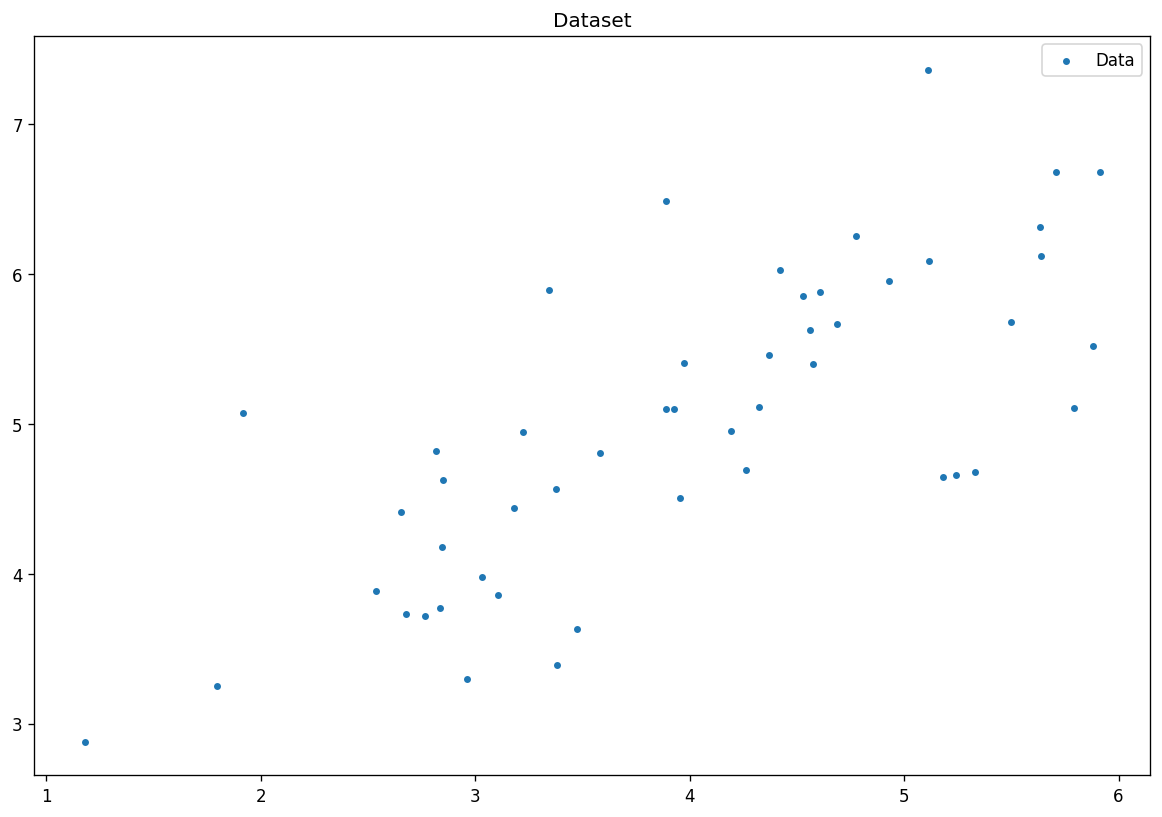
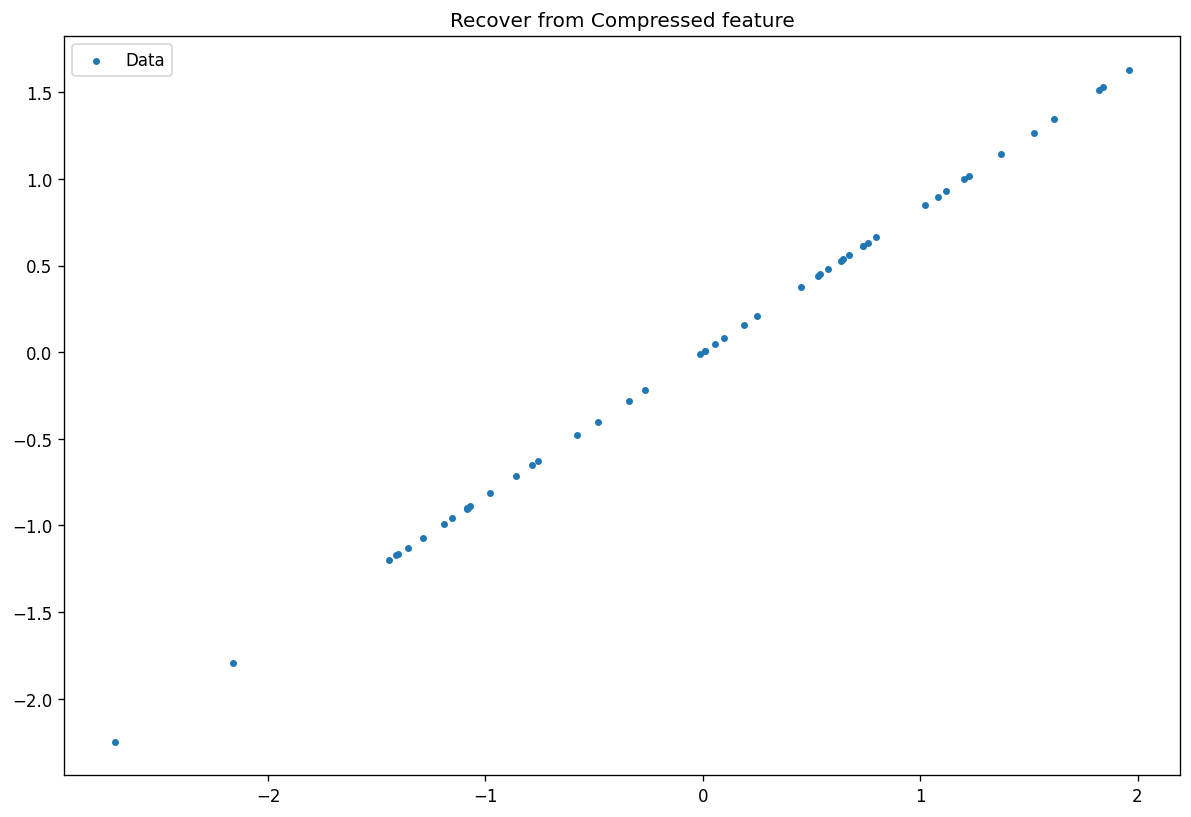
进行PCA降维可视化数据

from PCA import PCA
m_pca = PCA(1)
m_pca.fit(x)
x_reduced = m_pca.transform(x)
print("The principal axes of components is: {}\n"
      "The variance of each components is: {}\n"
      "The variance ratio of selected components is: {}"
      .format(m_pca.components_.tolist(), m_pca.explained_variance_.tolist(), m_pca.explained_variance_ratio_.tolist()))

The principal axes of components is: [[-0.7690815341368202], [-0.6391506816469459]]
The variance of each components is: [2.1098781795840327]
The variance ratio of selected components is: [0.8706238489732337]

3.1 进行人脸数据压缩

展示人脸数据

faces = loadmat('data/ex7faces.mat')
face_x = faces['X']
face_x.shape

(5000, 1024)

可以看到共5000张人脸数据维度是1024维度。

使用PCA降维到100维度

from PCA import PCA
face_pca = PCA(n_components=100)
face_pca.fit(face_x)
face_r = face_pca.transform(face_x)

可以看到保留了大部分的人脸特征。