Dijkstra详解
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
简述:
让我们考虑一下没有负边的情况。在Bellman-Ford算法中,如果dp[i]还不是最短距离的话,那么即使进行dp[j]=d[i]+(从I 到j的边的权值)的更新,dp[j]也不会变成最短距离。而且,即使dp[i]没有变化,每一次循环也要检查-遍从出发的所有边。这显然是很浪费时间的。因此可以对算法做如下修改。
(1)找到最短距离已经确定的顶点,从它出发更新相邻顶点的最短距离。
(2)此后不需要再关心1中的“最短距离已经确定的顶点”。
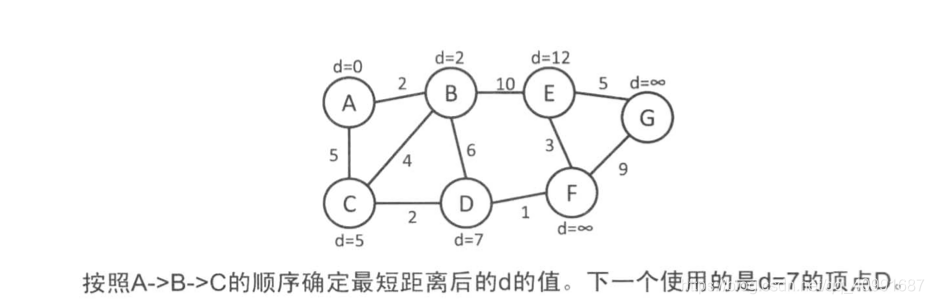
定义:
在(1)和(2)中提到的“最短距离已经确定的顶点”要怎么得到是问题的关键。在最开始时,只有起点的最短距离是确定的。而在尚未使用过的顶点中,距离dp[i]最 小的顶点就是最短距离已经确定的顶点。这是因为由于不存在负边,所以dp[i]不会在之后的更新中变小。这个算法叫做Dijkstra算法。
优化一:
使用邻接矩阵实现的Djkstra算法的复杂度是O(V^2)。使用邻接表的话,更新最短距离只需要访问
每条边一次即可,因此这部分的复杂度是O(E)。但是每次要枚举所有的顶点来查找下一个使用
的顶点,因此最终复杂度还是O(v^2)。在E比较小时,大部分的时间花在了查找下一个使用的顶
点上,因此需要使用合适的数据结构对其进行优化。首先想到了集合,使用vector来模拟集合即可。
实现:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int n,m;//n个顶点m条边
const int INF=1e9;
vector<vector<int>>mp(1003,vector<int>(1003,INF));
vector<int>dp(1003,INF);
vector<int>unused;
void Dijkstra(int s) {
dp[s]=0;
unused.resize(n);
for(int i=0; i<n; ++i)
unused[i]=i;
while(1) {
int v=-1;
for(int i=0; i<unused.size(); ++i)
if((v==-1||dp[unused[i]]<dp[v]))//在没使用的顶点集中寻找离生成集合最近的点
v=unused[i];
if(v==-1)//若已没有没使用的点了,证明最短路径已全部更新完毕
break;
unused.erase(find(unused.begin(),unused.end(),v));//加入找到的点到生成集合中
for(int i=0; i<unused.size(); ++i)
dp[unused[i]]=min(dp[unused[i]],dp[v]+mp[v][unused[i]]);//更新因该点而改变未使用的点的最小dp值
}
}
int main() {
cin>>n>>m;
for(int i=0; i<m; ++i) {
int a,b,c;
cin>>a>>b>>c;
mp[a][b]=c;
mp[b][a]=c;
}
int s;
cin>>s;
Dijkstra(s);
for(int i=0; i<n; ++i)
cout<<dp[i]<<" ";
}
优化二:
需要优化的是数值的插入(更新)和取出最小值两个操作,因此使用堆就可以了。把每个顶点当
前的最短距离用堆维护,在更新最短距离时,把对应的元素往根的方向移动以满足堆的性质。而
每次从堆中取出的最小值就是下一次要使用的顶点。这样堆中元素共有O(V)个,更新和取出数
值的操作有0(E)次,因此整个算法的复杂度是O(E *logV )。
下面是使用STL的priority_ queue 的实现。在每次更新时往堆里插人当前最短距离和顶点的值对。插入的次数是O(E)次,因此元素也是O(E)个。当取出的最小值不是最短距离的话,就丢弃这个值。这样整个算法也可以在同样的复杂度内完成。
来一个Pro版本:
#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
int n,m;//n个顶点m条边
const int INF=1e9;
typedef pair<int,int> p;//first为dp值,second为顶点号
vector<vector<int>>mp(1003,vector<int>(1003,INF));
vector<int>dp(1003,INF);
vector<int>used(1003,0);
void Dijkstra_Pro(int s) {
dp[s]=0;
priority_queue<p,vector<p>,greater<p>> q;
q.push(p(0,s));
while(!q.empty()) {
p temp=q.top();
q.pop();
int v=temp.second;
if(dp[v]<temp.first)//如果其最新dp值与过去的某一个更新时保存的dp值大小不一时放弃选择,因为过去的dp值已无效。
continue;
used[v]=1;
for(int i=0; i<n; ++i)
if(!used[i]) {
int t=dp[i];
dp[i]=min(dp[i],dp[v]+mp[v][i]);//更新因该点而改变未使用的点的最小dp值
if(t!=dp[i])//当且仅当dp[i]已更新时才加入优先队列中
q.push(p(dp[i],i));
}
}
}
int main() {
cin>>n>>m;
for(int i=0; i<m; ++i) {
int a,b,c;
cin>>a>>b>>c;
mp[a][b]=c;
mp[b][a]=c;
}
int s;
cin>>s;
Dijkstra_Pro(s);
for(int i=0; i<n; ++i)
cout<<dp[i]<<" ";
}
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

