【从零开始学习深度学习】39. 梯度下降优化之动量法介绍及其Pytorch实现

1. 梯度下降中的问题

假设输入为二维向量$\mathbf{x}=[x_1,x_2{]}^{\top }$输出为标量的目标函数$f(\mathbf{x})=0.1x_1^2+2x_2^2$。下面实现基于这个目标函数的梯度下降并演示使用学习率为$0.4$时自变量的迭代轨迹。

%matplotlib inline
import sys 
import d2lzh_pytorch as d2l
import torch

eta = 0.4 # 学习率

def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2

def gd_2d(x1, x2, s1, s2):
    # 自变量更新x-eta*dx
    return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)

d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

输出

epoch 20, x1 -0.943467, x2 -0.000073

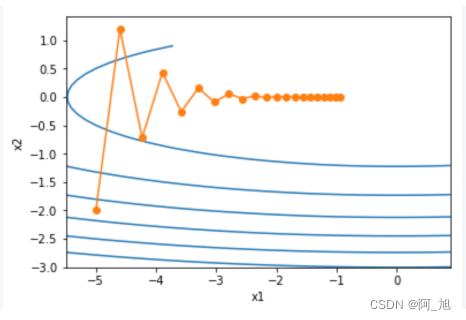
可以看到同一位置上目标函数在竖直方向$x_2$轴方向比在水平方向$x_1$轴方向的斜率的绝对值更大。因此给定学习率梯度下降迭代自变量时会使自变量在竖直方向比在水平方向移动幅度更大。那么我们需要一个较小的学习率从而避免自变量在竖直方向上越过目标函数最优解。然而这会造成自变量在水平方向上朝最优解移动变慢。

下面我们试着将学习率调得稍大一点此时自变量在竖直方向不断越过最优解并逐渐发散。

eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

输出

epoch 20, x1 -0.387814, x2 -1673.365109

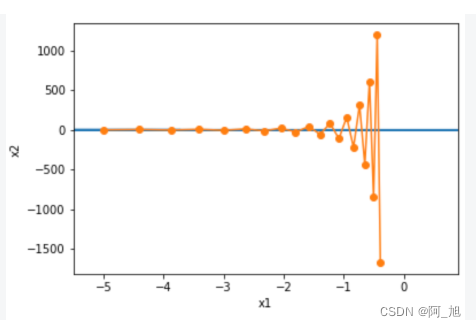
2. 动量法介绍及原理

动量法的提出是为了解决梯度下降的上述问题。设时间步$t$的自变量为${\mathbf{x}}_t$学习率为${\eta }_t$。在时间步$0$动量法创建速度变量${\mathbf{v}}_0$并将其元素初始化成0。在时间步$t>0$动量法对每次迭代的步骤做如下修改
$$\begin{array}{rl}{\mathbf{v}}_t& \leftarrow \gamma {\mathbf{v}}_{t-1}+{\eta }_t{\mathbf{g}}_t,\\ {\mathbf{x}}_t& \leftarrow {\mathbf{x}}_{t-1}-{\mathbf{v}}_t,\end{array}$$

其中动量超参数$\gamma$满足$0\le \gamma <1$。${\mathbf{g}}_t$为小批量随机梯度。当$\gamma =0$时动量法等价于小批量随机梯度下降。

我们先观察一下梯度下降在使用动量法后的迭代轨迹。

def momentum_2d(x1, x2, v1, v2):
    v1 = gamma * v1 + eta * 0.2 * x1
    v2 = gamma * v2 + eta * 4 * x2
    return x1 - v1, x2 - v2, v1, v2

eta, gamma = 0.4, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

输出

epoch 20, x1 -0.062843, x2 0.001202

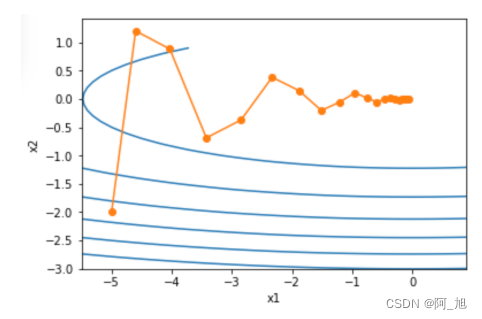
可以看到使用较小的学习率$\eta =0.4$和动量超参数$\gamma =0.5$时动量法在竖直方向上的移动更加平滑且在水平方向上更快逼近最优解。下面使用较大的学习率$\eta =0.6$此时自变量也不再发散。

eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

输出

epoch 20, x1 0.007188, x2 0.002553

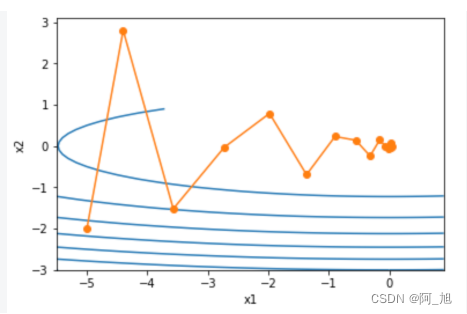
2.1 动量法的数学解释—指数加权移动平均

为了从数学上理解动量法让我们先解释一下指数加权移动平均exponentially weighted moving average。给定超参数$0\le \gamma <1$当前时间步$t$的变量$y_t$是上一时间步$t-1$的变量$y_{t-1}$和当前时间步另一变量$x_t$的线性组合

$$y_t=\gamma y_{t-1}+(1-\gamma )x_t.$$

我们可以对$y_t$展开

$$\begin{array}{rl}{y}_t& =(1-\gamma )x_t+\gamma y_{t-1}\\ & =(1-\gamma )x_t+(1-\gamma )\cdot \gamma x_{t-1}+{\gamma }^2{y}_{t-2}\\ & =(1-\gamma )x_t+(1-\gamma )\cdot \gamma x_{t-1}+(1-\gamma )\cdot {\gamma }^2{x}_{t-2}+{\gamma }^3{y}_{t-3}\\ & \dots \end{array}$$

令$n=1/(1-\gamma )$那么 ${\left(1-1/n\right)}^n={\gamma }^{1/(1-\gamma )}$。因为

$$\underset{n\to \infty }{\lim }{\left(1-\frac{1}{n}\right)}^n=\exp (-1)\approx 0.3679,$$

所以当$\gamma \to 1$时${\gamma }^{1/(1-\gamma )}=\exp (-1)$如$0.95^{20}\approx \exp (-1)$。如果把$\exp (-1)$当作一个比较小的数我们可以在近似中忽略所有含${\gamma }^{1/(1-\gamma )}$和比${\gamma }^{1/(1-\gamma )}$更高阶的系数的项。例如当$\gamma =0.95$时

$$y_t\approx 0.05\sum _{i=0}^{19}0.95^i{x}_{t-i}.$$

因此在实际中我们常常将$y_t$看作是对最近$1/(1-\gamma )$个时间步的$x_t$值的加权平均。例如当$\gamma =0.95$时$y_t$可以被看作对最近20个时间步的$x_t$值的加权平均当$\gamma =0.9$时$y_t$可以看作是对最近10个时间步的$x_t$值的加权平均。而且离当前时间步$t$越近的$x_t$值获得的权重越大越接近1。

2.2 由指数加权移动平均理解动量法

现在我们对动量法的速度变量做变形

$${\mathbf{v}}_t\leftarrow \gamma {\mathbf{v}}_{t-1}+(1-\gamma )\left(\frac{{\eta }_t}{1-\gamma }{\mathbf{g}}_t\right).$$

由指数加权移动平均的形式可得速度变量${\mathbf{v}}_t$实际上对序列 { η t − i g t − i / ( 1 − γ ) : i = 0 , … , 1 / ( 1 − γ ) − 1 } \{\eta_{t-i}\boldsymbol{g}_{t-i} /(1-\gamma):i=0,\ldots,1/(1-\gamma)-1\} {ηt−i​gt−i​/(1−γ):i=0,…,1/(1−γ)−1}做了指数加权移动平均。换句话说相比于小批量随机梯度下降动量法在每个时间步的自变量更新量近似于将最近$1/(1-\gamma )$个时间步的普通更新量即学习率乘以梯度做了指数加权移动平均后再除以$1-\gamma$。所以在动量法中自变量在各个方向上的移动幅度不仅取决当前梯度还取决于过去的各个梯度在各个方向上是否一致。这样我们就可以使用较大的学习率从而使自变量向最优解更快移动。

3. 从零实现动量法

相对于小批量随机梯度下降动量法需要对每一个自变量维护一个同它一样形状的速度变量且超参数里多了动量超参数。实现中我们将速度变量用更广义的状态变量states表示。

features, labels = d2l.get_data_ch7()

def init_momentum_states():
    v_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
    v_b = torch.zeros(1, dtype=torch.float32)
    return (v_w, v_b)

def sgd_momentum(params, states, hyperparams):
    for p, v in zip(params, states):
        v.data = hyperparams['momentum'] * v.data + hyperparams['lr'] * p.grad.data
        p.data -= v.data

我们先将动量超参数momentum设0.5这时可以看成是特殊的小批量随机梯度下降其小批量随机梯度为最近2个时间步的2倍小批量梯度的加权平均。

d2l.train_ch7(sgd_momentum, init_momentum_states(),
              {'lr': 0.02, 'momentum': 0.5}, features, labels)

输出

loss: 0.245518, 0.042304 sec per epoch

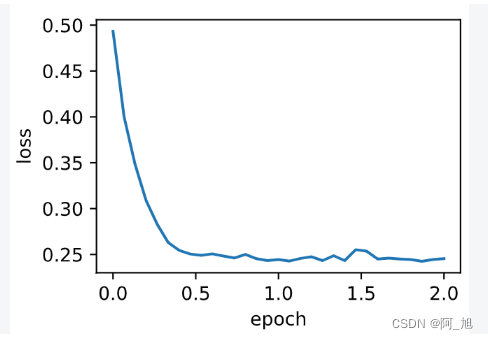
将动量超参数momentum增大到0.9这时依然可以看成是特殊的小批量随机梯度下降其小批量随机梯度为最近10个时间步的10倍小批量梯度的加权平均。我们先保持学习率0.02不变。

d2l.train_ch7(sgd_momentum, init_momentum_states(),
              {'lr': 0.02, 'momentum': 0.9}, features, labels)

输出

loss: 0.252046, 0.095708 sec per epoch

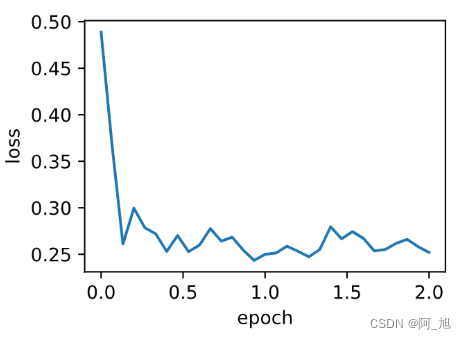
可见目标函数值在后期迭代过程中的变化不够平滑。直觉上10倍小批量梯度比2倍小批量梯度大了5倍我们可以试着将学习率减小到原来的1/5。此时目标函数值在下降了一段时间后变化更加平滑。

d2l.train_ch7(sgd_momentum, init_momentum_states(),
              {'lr': 0.004, 'momentum': 0.9}, features, labels)

输出

loss: 0.242905, 0.073496 sec per epoch

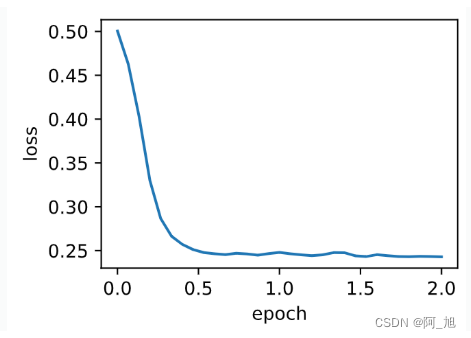
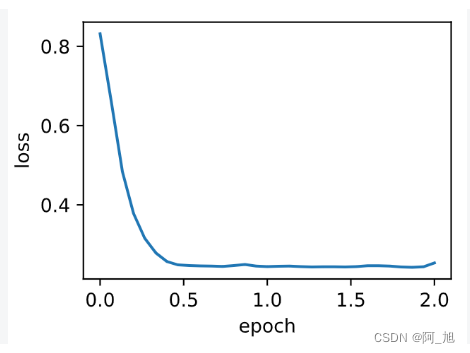
4. 基于Pytorch简洁实现动量法

在PyTorch中只需要通过参数momentum来指定动量超参数即可使用动量法。

d2l.train_pytorch_ch7(torch.optim.SGD, {'lr': 0.004, 'momentum': 0.9},
                    features, labels)

输出

loss: 0.253280, 0.060247 sec per epoch

总结

• 动量法使用了指数加权移动平均的思想。它将过去时间步的梯度做了加权平均且权重按时间步指数衰减。
• 动量法使得相邻时间步的自变量更新在方向上更加一致。

---

如果文章内容对你有帮助感谢点赞+关注

欢迎关注下方GZH阿旭算法与机器学习共同学习交流~