平面电磁波的反射与折射，极化滤波作用

阿里云国际版折扣https://www.yundadi.com

阿里云国际，腾讯云国际，低至75折。AWS 93折免费开户实名账号代冲值优惠多多微信号：monov8 飞机：@monov6

引言

反射定律和折射定律

反射系数和折射系数

平面电磁波在理想介质分界面上的全反射和全折射

引言

再复杂的电磁波我们都可以看作是很多平面电磁波的叠加

我们在前面介绍的时候我们认为传播的空间是无限大的

我们的水流如果在流动的过程中我们会看到流体的流动会发生一些变化我们在流体里面把木头棒称作障碍物两种介质的分界面我们也可以理解为障碍物

我们假设分片均匀在穿过的时候磁导率发生了突变在外电场的作用下会发生极化在表面上会出现一层面极化电荷这些电荷他要产生电场如果是时变电磁波的作用下媒质会产生磁化会出现面磁化电流也会产生随着时间变化的电磁场

我们媒质的分界面就是障碍物媒质特性发生突变的地方就是障碍物

实际上飞机就是一个障碍物

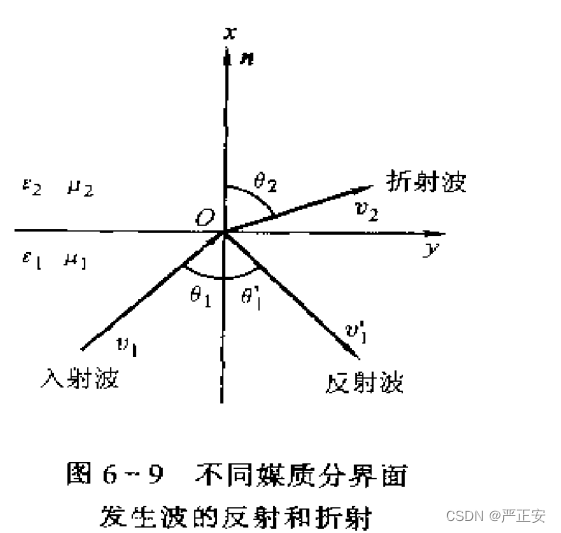
但是我们知道障碍物表面的形状可能很复杂我们研究在分界面两侧折射波和反射波的关系

入射波与法线的夹角为 $\theta_1$

折射波与法线的夹角为 $\theta_2$

现在我们知道了入射波的电场强度

我们要确定的是反射波传播的方向和法线的夹角

折射波传播的方向和法线的夹角

反射定律和折射定律

电磁场里面所谓的衔接条件电场强度的切向分量要连续在分界面上假设没有面传导电流

磁化以后会产生面磁化电流但并不影响

$v_1 \Delta t =v_y \Delta t sin(\theta _1)$

我们得到

$v_y=\frac{v_1}{sin\theta_1}$

依次可以推出

$\frac{v_1}{sin \theta_1}=\frac{v_1^{\prime}}{sin \theta_1^{\prime}}=\frac{v_2}{sin \theta_2}$

我们再看由于入射波反射波都在媒质1中前进

所以 $v_1^{\prime}=v_1$

由此我们得到

$\theta_1^{\prime}=\theta_1$

所以我们得到

$\frac{sin\theta_2}{sin \theta_1}=\frac{v_2}{v_1}$

$v_2=\frac{1}{\sqrt{\mu_2 \varepsilon_2}}$

我们得到

$\frac{sin\theta_2}{sin\theta_1}=\sqrt{\frac{\mu_1 \varepsilon_1}{\mu_2 \varepsilon_2}}$

我们把这个定律称为折射定律这就是所谓的斯奈尔定律

由于我们的波碰到了介质分界面透过分界面前进的时候产生改变

如果是非磁性媒质

$\mu_1 =\mu_2=\mu_0$

$\frac{sin \theta_2}{sin \theta_1}=\sqrt{\frac{\varepsilon_1}{\varepsilon_2}}$

这就是我们的斯奈尔定律

反射系数和折射系数

这是我们两种媒质的分界面

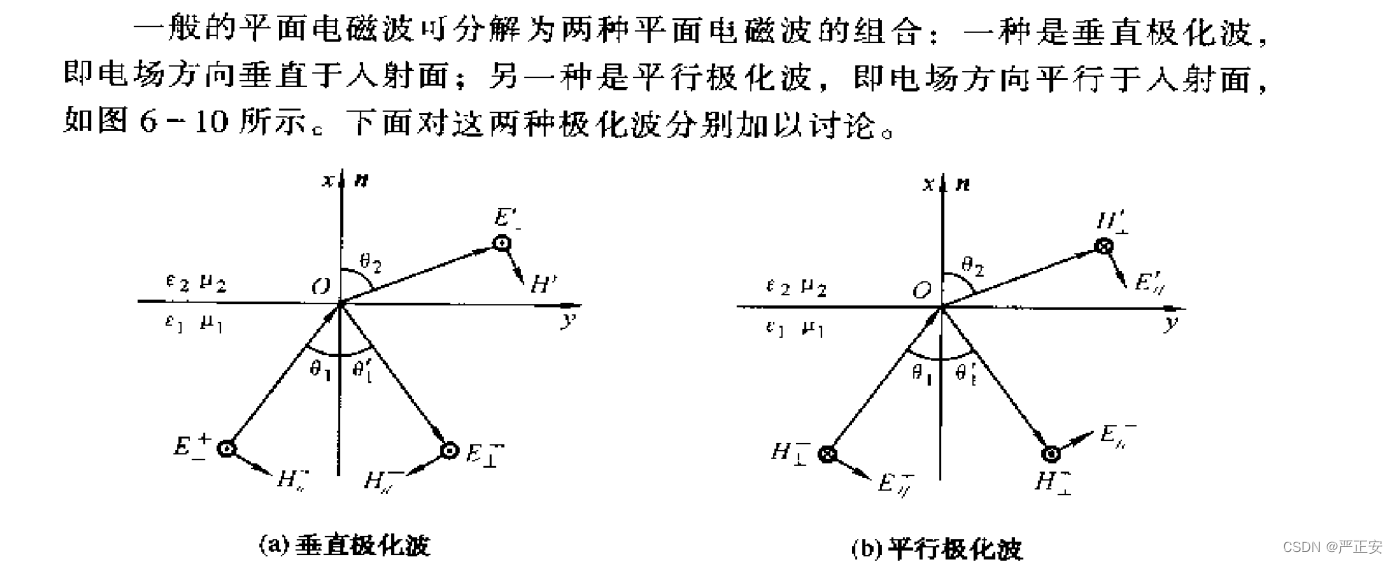
我们可以把一般的平面电磁波看作是两种平面电磁波的组合一种是垂直极化波即电场方向垂直于入射面另一种是平行极化波即电场方向平行于入射面

我们假设

$\frac{E_{\perp}^{+}}{H_{\parallel}^{+}}=Z_{01}$

$\frac{E_{\perp}^{-}}{H_{\parallel}^{-}}=Z_{01}$

$\frac{E_{\perp}^{\prime}}{H_{\parallel^{\prime}}}=Z_{02}$

$Z_{01}=\sqrt{\frac{\mu_1}{\varepsilon_1}}$

$Z_{02}=\sqrt{\frac{\mu_2}{\varepsilon_2}}$

在我们的媒质分界面上如果没有面传导电流

$E_{2t}=E_{1t},H_{2t}=H_{1t}$

入射波和分界面相切我们看到这时候

$E_{\perp}^{+}+E_{\perp}^{-}=E_{\perp}^{\prime}$

我们磁场强度的切向分量要连续

磁场强度的切向分量

$H_{\parallel}^{+} cos \theta_1 - H_{\parallel}^{-} cos \theta_1=H_{\parallel}^{\prime} cos \theta_2$

$\gamma_{\perp}=\frac{E_{\perp}^{-}}{E_{\perp}^{+}}=\frac{Z_{02} cos \theta_1 -Z_{01} cos \theta_2}{Z_{02} cos \theta_1 + Z_{01} cos \theta_2}$ 我们称之为反射系数

我们还可以得到

$T_{\perp}=\frac{E_{\perp}^{\prime}}{E_{\perp}^{+}}=2\frac{Z_{02} cos \theta_1 }{Z_{02} cos \theta_1 + Z_{01} cos \theta_2}$ 这是分界面上的折射系数

同理我们可以得到

$\gamma_{\parallel}=\frac{E_{\parallel}^{-}}{E_{\parallel}^{+}}=\frac{Z_{02} cos \theta_2 -Z_{01} cos \theta_1}{Z_{02} cos \theta_2 + Z_{01} cos \theta_1}$

$T_{\parallel}=\frac{E_{\perp}^{\prime}}{E_{\parallel}^{+}}=2\frac{Z_{02} cos \theta_1 }{Z_{02} cos \theta_2 + Z_{01} cos \theta_1}$

我们把这个称为菲涅尔公式

平面电磁波在理想介质分界面上的全反射和全折射

全反射

$|\gamma_{\perp}|=1$ 或者 $|\gamma_{\parallel}|=1$

如果 $\theta_1 \neq 90^{\circ}$ 应取 $cos \theta_2=0$

这个时候两个反射系数等于1

我们可以推出

$\theta_2=90^{\circ}$

这个时候就发生了全反射

$sin \theta_2 =\sqrt{\frac{\mu_1 \varepsilon_1}{\mu_2 \varepsilon_2}}sin \theta_1$

当 $\theta_1=\theta_c$ 称为临界角如果两边都是非磁性介质

$\mu_1 =\mu_2 \approx \mu_0$

我们可以得到

$sin \theta_2=\sqrt{\frac{\varepsilon_2}{\varepsilon_1}}$

此时 $\varepsilon_2 <\varepsilon_1$ 从光密介质射向光疏介质

这就是一种典型的表面波

我们把介质的分界面也可以看作表面波导

如果我们在传输电磁波的时候可以人为设置分界面让电磁波沿着界面传播

光纤就是利用的就是这个原理实际上是一种光波导如果我们现在有一个介质棒

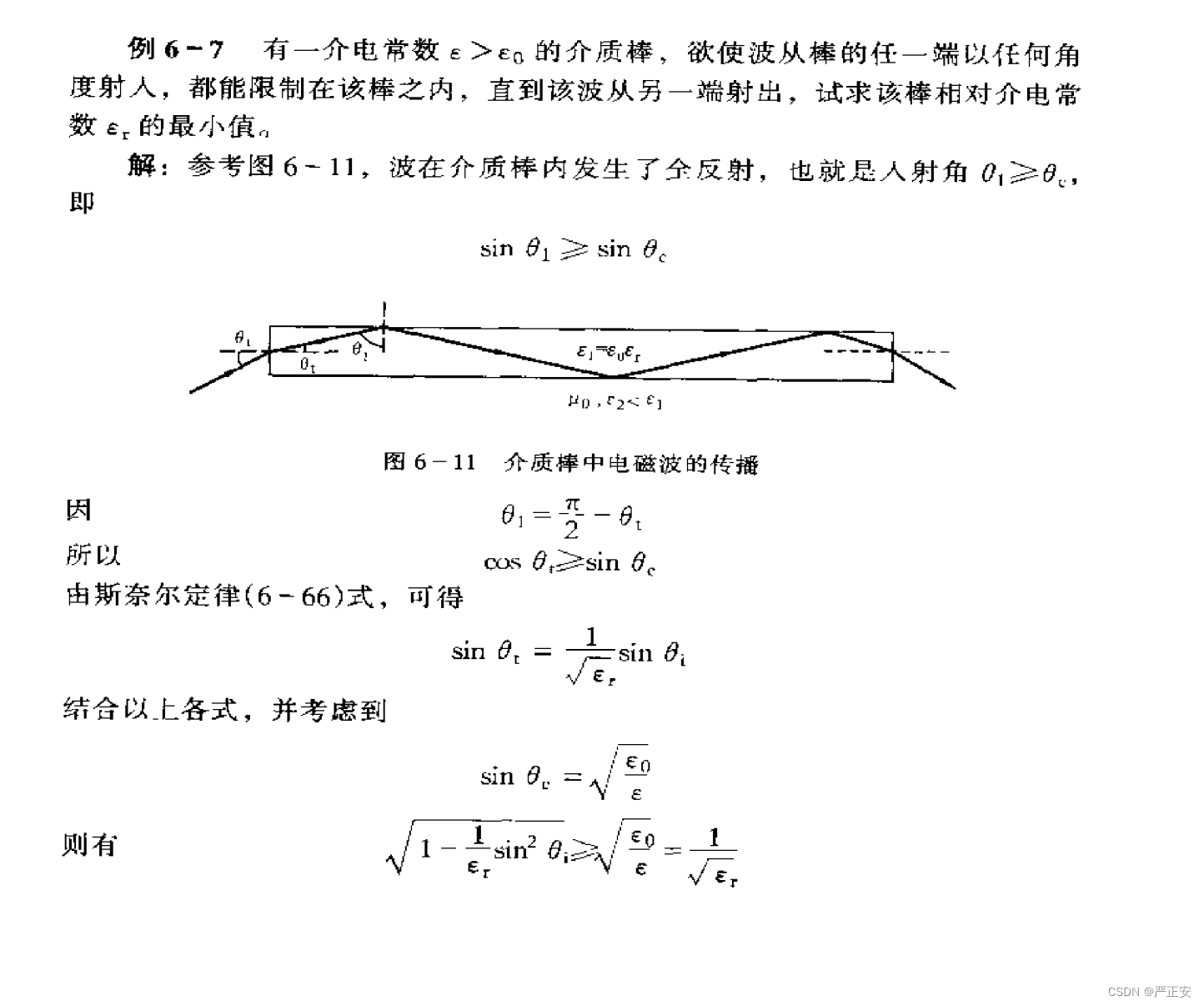
全折射

对于非磁性媒质来说

$\sqrt{\frac{\varepsilon_1}{\varepsilon_2}} cos \theta_1 =\sqrt{1- sin^{2} \theta_2}$

现在我们根据斯奈尔定律

$\frac{sin\theta_2}{sin \theta_1}=\sqrt{ \frac{\varepsilon_1}{\varepsilon_2}}$

代入我们可以得到

$\sqrt{\frac{\varepsilon_1}{\varepsilon_2}} cos \theta_1 =\sqrt{1-\frac{\varepsilon_1}{\varepsilon_2}sin^{2} \theta_1}$

$\frac{\varepsilon_1}{\varepsilon_2}=1$

换句话说两种非磁性的媒质

对于垂直极化波在非磁性媒质中不可能发生全折射

入射角不管怎么样调整或多或少在媒质里面都有反射波

调整了一个角度以后会小一些但是绝对消除不了

我们再看平行极化波

我们说如果要让 $\gamma_{\parallel}=0$

我们应该要让

$Z_{02} cos \theta_2 =Z_{01} cos \theta_1$

对于非磁性媒质我们得到

$\sqrt{\frac{\varepsilon_2}{\varepsilon_1}}cos \theta_1 = cos \theta_2=\sqrt{1-sin^2 \theta_2}$

所以我们得到

$\sqrt{\frac{\varepsilon_2}{\varepsilon_1}} cos \theta_1 =\sqrt{1-\frac{\varepsilon_1}{\varepsilon_2}sin^{2} \theta_1}$

现在这个公式也非常简单我们把这个换成

$\sqrt{\frac{\varepsilon_2}{\varepsilon_1}} \sqrt{1-sin^2 \theta_1}=\sqrt{1-\frac{\varepsilon_1}{\varepsilon_2}sin^{2} \theta_1}$

我们解得

$sin \theta_1 =\sqrt{\frac{\varepsilon_2}{\varepsilon_1 +\varepsilon_2}}$

我们得到

$tan \theta_1 =\sqrt{\frac{\varepsilon_2}{\varepsilon_1}}$

极化滤波作用

我们一般把这个角度称作布鲁斯特角也叫做起偏角

现在有一个电磁波既有垂直于平面的电场分量也有平行的电场分量

如果我们现在需要滤波把垂直平面波和平行平面波分离开来

如果现在角度就是 $\theta_B$

平行极化波到这个分界面全部折射到第二个介质里面

但是垂直极化波或多或少就会有反射波在反射波里面只有垂直极化波分量

这就起到了分离作用这个称之为极化滤波作用

我们有时候把 $\theta_B$ 称为起偏角

平面电磁波在良导体上的反射与折射

如果现在我们有一个良导体

如果现在我们有一个良导体它的电导率非常大我们如果把良导体设想成一种理想介质 $\frac{sin \theta_2}{sin \theta_1}=\frac{v_2}{v_1}$

$sin \theta_2=\frac{v_2}{v_1} sin \theta_1$

我们回想一下在理想介质里面传播常数是 $\frac{1}{\mu_1 \varepsilon_1}$

良导体里面的波速是 $\frac{2 \omega}{\mu_2 \gamma}$

我们得到

$sin \theta_2 =\sqrt{\frac{2 \omega \varepsilon}{\gamma}} sin\theta_1 \approx 0$

$\theta_2 \approx 0$

良导体里面电磁波都是垂直于分界面前进的

只要入射角不等于90度我们再根据媒质2的波阻抗我们近似可以得到

$\Gamma_{\parallel} \approx -1,\Gamma_{\perp}\approx -1$

在良导体表面上反射波的电场和入射波的电场在大小上近似相等在相位上近似相反

阿里云国际版折扣https://www.yundadi.com

阿里云国际，腾讯云国际，低至75折。AWS 93折免费开户实名账号代冲值优惠多多微信号：monov8 飞机：@monov6

返回列表

上一篇：八股文总结

下一篇：kotlin之面向对象

“平面电磁波的反射与折射，极化滤波作用” 的相关文章

手把手教你使用LabVIEW实现Mask R-CNN图像实例分割1年前 (2023-02-02)

Vue+echart 展示后端获取的数据1年前 (2023-02-02)

2022圣诞代码合集(圣诞树+圣诞老人)1年前 (2023-02-02)

【Azure 存储服务】.NET7.0 示例代码之上传大文件到Azure Storage Blob1年前 (2023-02-02)

【速记】C++ STL自定义排序1年前 (2023-02-02)

【单片机/嵌入式】最完整学习路线_嵌入式单片机学习过程1年前 (2023-02-02)

浅谈PHP设计模式的命令模式1年前 (2023-02-02)

一名普通Java程序员的2022的总结和2023的展望_程序员未来展望1年前 (2023-02-02)

[概率论与数理统计]笔记：4.4 抽样分布1年前 (2023-02-02)

VMware虚拟机安装Linux教程(超详细)1年前 (2023-02-02)