【高阶数据结构】海量数据如何处理? (位图 & 布隆过滤器)
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
🌈欢迎来到高阶数据结构专栏~~位图 & 布隆过滤器
- (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort
- 目前状态大三非科班啃C++中
- 🌍博客主页张小姐的猫~江湖背景
- 快上车🚘握好方向盘跟我有一起打天下嘞
- 送给自己的一句鸡汤🤔
- 🔥真正的大师永远怀着一颗学徒的心
- 作者水平很有限如果发现错误可在评论区指正感谢🙏
- 🎉🎉欢迎持续关注

文章目录

一. 引入
先来道面试题
🔥给40亿个不重复的无符号整数没排过序给一个无符号整数如何快速的判断这个数是否在这40亿个数中
- 40亿个无符号整数的空间是大概是
16G- 1️⃣搜索树和哈希表都不太行。因为内存放不下搜索树不仅仅只有数据还有三个指针和一个标记颜色大小起码还要
*4哈希表还要2~3倍的空间 - 2️⃣排序+ 二分查找呢效率
log(N)但问题并不在于你搜索这个数字的效率问题而是你在遍历也好排序也罢这些数字在内存中放的下么只能存在磁盘文件上数据在磁盘上效率慢
- 1️⃣搜索树和哈希表都不太行。因为内存放不下搜索树不仅仅只有数据还有三个指针和一个标记颜色大小起码还要
接下来引入一个boss位图
二. 位图模型
我们表示一个数据在还是不在只需要一个标记值就可以不需要真正的把这个值存储起来使用直接定值法一个比特位映射标记值1就是在0就是不在
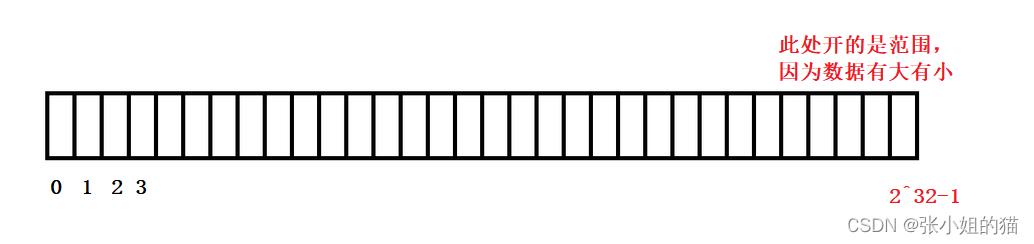
那么此处的空间大小是多少呢因为开的是bit位一个字节有8个比特位4g除8后只需512mb就可以完成效率嘎嘎高
记住我们开的是范围而不是数据的个数
三. 设计位图
为了方便我们将位图用一个数组表示让vector帮我们开辟一段连续的空间我们只负责将数据设置或者移除就行
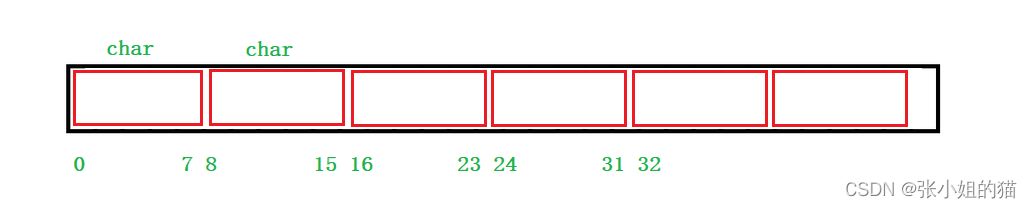
template<size_t N>
class bitset
{
public:
bitset()
{
_bits.resize(N/8+1, 0);//永远多开一个char防止N过小比如10
}
private:
vector<char> _bits;
};
1️⃣set标记
举例x = 20
在第几个charx / 8
在这个char里的第几个比特位x%8

void set(size_t x)
{
size_t i = x / 8;//在哪个char
size_t j = x % 8;//在char中的具体位置
_bits[i] |= (1 << j);
}
2️⃣reset取消标记
为了表达j位为0必须先取反在与比较处理后的j位必须为0

void reset(size_t x)
{
size_t i = x / 8;//在哪个char
size_t j = x % 8;//在char中的具体位置
_bits[i] &= ~(1 << j);//先取反 再与
}
3️⃣test检查
很简单把j位的数据与&上即可判断是否存在数据
bool test(size_t x)
{
size_t i = x / 8;//在哪个char
size_t j = x % 8;//在char中的具体位置
return _bits[i] & (1 << j);
}
完整代码
namespace ljj
{
template<size_t N>
class bitset
{
public:
bitset()
{
_bits.resize(N/8+1, 0);
}
void set(size_t x)
{
size_t i = x / 8;//在哪个char
size_t j = x % 8;//在char中的具体位置
_bits[i] |= (1 << j);
}
void reset(size_t x)
{
size_t i = x / 8;//在哪个char
size_t j = x % 8;//在char中的具体位置
_bits[i] &= ~(1 << j);
}
bool test(size_t x)
{
size_t i = x / 8;//在哪个char
size_t j = x % 8;//在char中的具体位置
return _bits[i] & (1 << j);
}
private:
vector<char> _bits;
};
}
四. 扩展问题
🌏给定100亿个整数设计算法找到只出现一次的整数
如何设计呢实际上是kv的统计次数搜索模型
使用两个位图来表示满足01的就是只出现了一次的整数
0次就是 00
1次就是 01
两次及以上就是 10
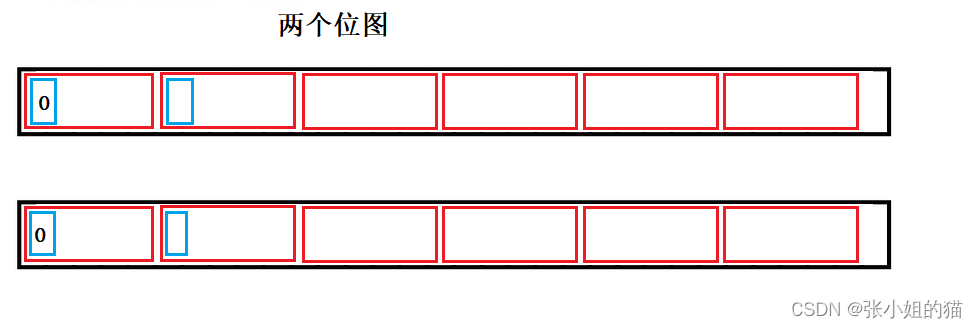
template<size_t N>
class twobitset
{
public:
void set(size_t x)
{
bool inset1 = _bs1.test(x);
bool inset2 = _bs2.test(x);
//00
if (inset1 == false && inset2 == false)
{
//00 -> 01 变成01
_bs2.set(x);
}
else if (inset1 == false && inset2 == true)
{
//01 -> 10
_bs1.set(x);
_bs2.reset(x);
}
}
void print_once_num()
{
for (size_t i = 0; i < N; i++)
{
if (_bs1.test(i) == false && _bs2.test(i) == true)
{
cout << i << endl;
}
}
}
private:
bitset<N> _bs1;
bitset<N> _bs2;
};
void test_bit_set3()
{
int a[] = { 3, 4, 5, 2, 3, 4, 4, 4, 4, 12, 77, 65, 44, 4, 44, 99, 33, 33, 33, 6, 5, 34, 12 };
twobitset<100> bs;
for (auto e : a)
{
bs.set(e);
}
bs.print_once_num();
}
记过如下
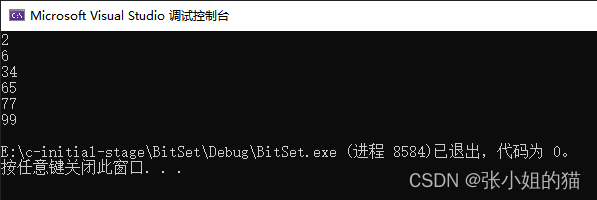
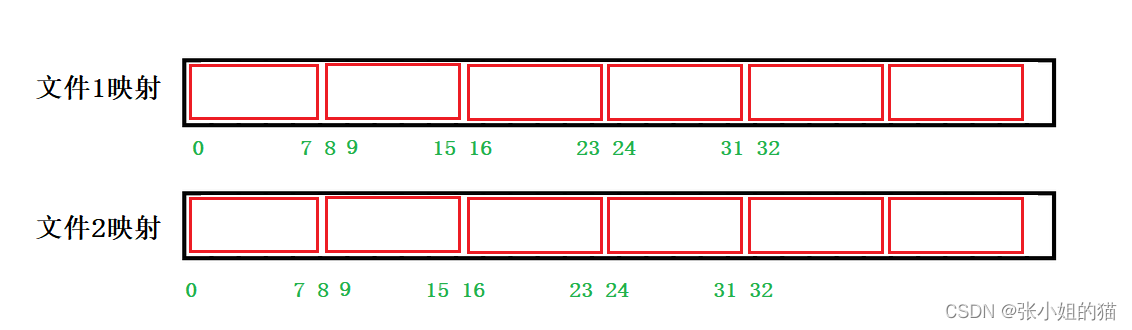
🌏给两个文件分别有100亿个整数我们只有1G内存如何找到两个文件的交集
两个文件中都存在的就是交集前提是要先去重
🌏一个文件有100亿个int1G内存设计算法找出出现次数不超过2次的所有整数
这题与上面的类似思路大近相同多判断一次把10->11,最后找不超过两次的整数
0次就是 00
1次就是 01
两次就是 10
三次及以上就是 11
void set(size_t x)
{
bool inset1 = _bs1.test(x);
bool inset2 = _bs2.test(x);
//00
if (inset1 == false && inset2 == false)
{
//00 -> 01 变成01
_bs2.set(x);
}
else if (inset1 == false && inset2 == true)
{
//01 -> 10
_bs1.set(x);
_bs2.reset(x);
}
else if(inset1 == true && inset2 == false)
{
//10 -> 11
_bs1.set(x);
_bs2.set(x);
}
}
位图特点
- 快节省空间直接定值法不存在冲突
- 相对局限只能映射整形
😎boss布隆过滤器
我们现实中也遇到过
比如王者荣耀中要新注册一个ID的时候你想到一个很有有趣的昵称但此时系统告诉你 “此昵称已被注册”这个昵称的唯一性就是运用了哈希的布隆过滤器他本质上是就是一个 key 的模型他只需要判断对象是否存在过就行。
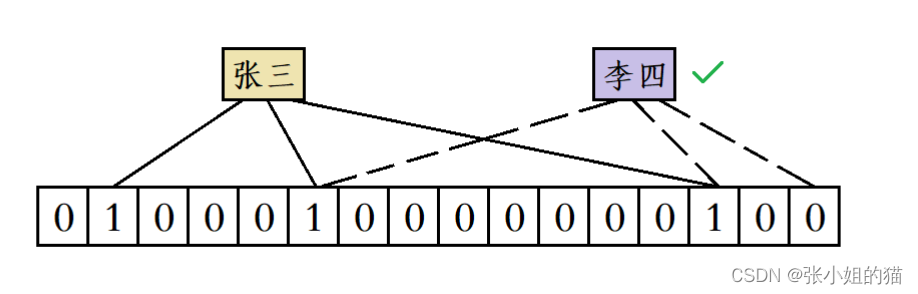
此时的布隆过滤器当仁不让布隆过滤器其实就是位图的一个变形和延申虽然无法避免哈希冲突但我们可以想办法降低误判的概率当一个数据映射到位图中时布隆过滤器会用多个哈希函数映射到多个比特位当判断一个数据是否在位图当中时需要分别根据这些哈希函数计算出对应的比特位比特位设置了代表着当前状态的默认值设置为 1 则判定为该数据存在
当然也存在误判
- 在不准确的存在误判
- 不在准确的不存在误判
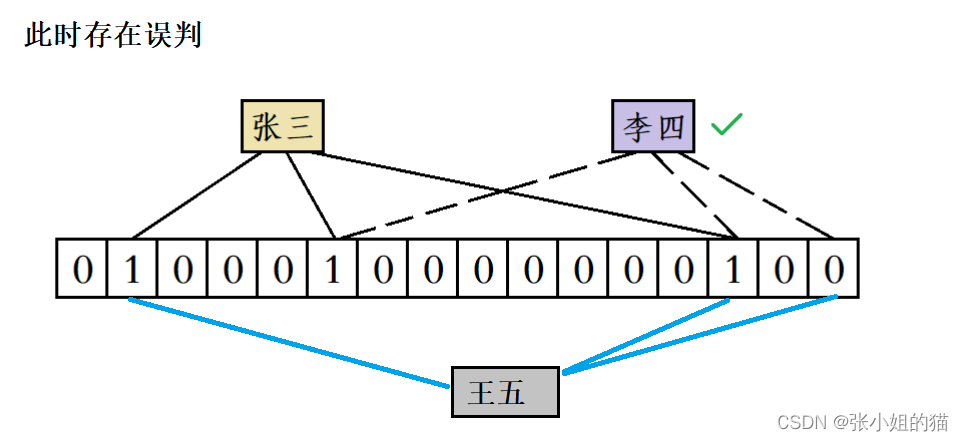
🎨重点
虽然布隆过滤器会出现误判因为这个数据的比特位被其他数据所占有但是判断一个数据不存在确实准确的不存在的就是0
🥑控制误判
不可能完全去掉误判只有尽可能的减少误判率
很显然过小的布隆过滤器比特位很快就会都被设为 1此时误判率就会飙升因此布隆过滤器的长度会直接影响误判率布隆过滤器的长度越长其误判率越小
理论而言一个值映射的位越多误判的概率越低但是不敢映射太多会造成空间消耗
大佬就此得出一个公式
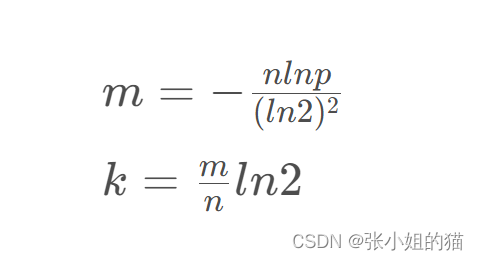
k 是哈希函数个数
m 为布隆过滤器长度
n为插入的元素个数
p为误判率
我们这里可以大概估算一下如果使用 3 个哈希函数那么 k 的值就为 3ln2 的值我们取 0.7那么 m 和 n 的关系大概是 m = 4.2 × n 也就是过滤器长度应该是插入元素个数的 4 倍
布隆的应用
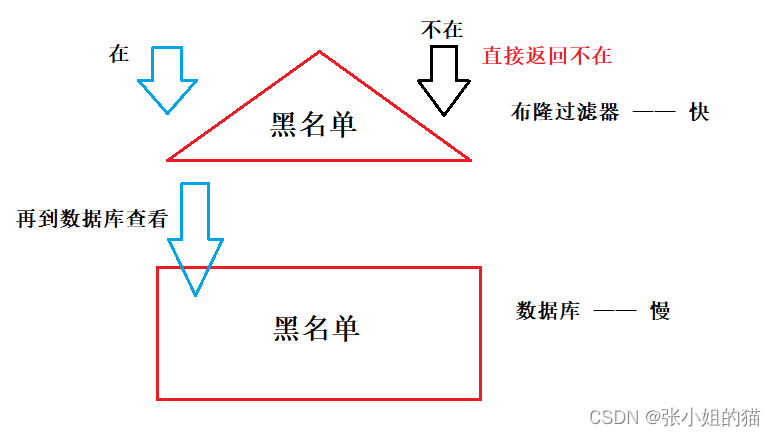
⚡具体实现
因为插入过滤器的元素不仅是字符串也可以是其他类型的数据只有调用者能够提供对应的哈希函数将该类型的数据转换成整型即可但一般情况下过滤器都是用来处理字符串的我们布隆过滤器可以实现为一个模板类所以这里可以将模板参数 T 的缺省类型设置为 string。
template<size_t N,
class T = string, class Hash1 = HashBKDR, class Hash2 = HashAP, class Hash3 = HashDJB>
class BloomFilter
{
public:
//...
private:
const static size_t _ratio = 5;
bitset<_ratio*N> _bits;
};
实例化布隆过滤器需要调用者提供三个哈希函数由于布隆过滤器一般处理的是字符串类型的数据因此这里我们可以默认提供几个将字符串转换成整型的哈希函数。
这里选取将字符串转换成整型的哈希函数是综合评分最高的 BKDRHash、APHash 和 DJBHash这三种哈希算法在多种场景下产生哈希冲突的概率是最小的
struct HashBKDR
{
// BKDR
size_t operator()(const string& key)
{
size_t val = 0;
for (auto ch : key)
{
val *= 131;
val += ch;
}
return val;
}
};
struct HashAP
{
// BKDR
size_t operator()(const string& key)
{
size_t hash = 0;
for (size_t i = 0; i < key.size(); i++)
{
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ key[i] ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ key[i] ^ (hash >> 5)));
}
}
return hash;
}
};
struct HashDJB
{
// BKDR
size_t operator()(const string& key)
{
size_t hash = 5381;
for (auto ch : key)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
🎃插入
布隆过滤器当中需要提供一个 set 接口用于插入元素插入元素时需要通过三个哈希函数分别计算出该元素对应的三个比特位然后在位图中设置为1即可
void Set(const T& key)
{
//key传给仿函数Hash1 变成整形
size_t i1 = Hash1()(key) % (_ratio * N);//数据不一定在范围里
_bits.set(i1);
size_t i2 = Hash2()(key) % (_ratio * N);
_bits.set(i2);
size_t i3 = Hash3()(key) % (_ratio * N);
_bits.set(i3);
}
🎃查找
检测时需要通过三个哈希函数分别计算出该元素对应的三个比特位然后判断这三个比特位是否被设置为1
思路
- 只要有一个比特位未被设置则说明该元素一定不存在准确的~ 反向判断一个为0就
false - 如果三个比特位全部被设置则返回 true 表示该元素存在可能仍存在误判
bool Test(const T& key)
{
size_t i1 = Hash1()(key) % _ratio * N;
//反向判断一个为0就false
if (!_bits.test(i1))
return false;//准确的
size_t i2 = Hash2()(key) % _ratio * N;
if (!_bits.test(i2))
return false;
size_t i3 = Hash3()(key) % _ratio * N;
if (!_bits.test(i3))
return false;
return true;//此处的在可能存在误判
}
🎃删除
布隆过滤器一般是不支持删除的
因为布隆过滤器判断一个元素存在时可能存在误判此时无法保证要删除的元素确实在过滤器当中此时将位图中对应的比特位清 0 会影响其他元素
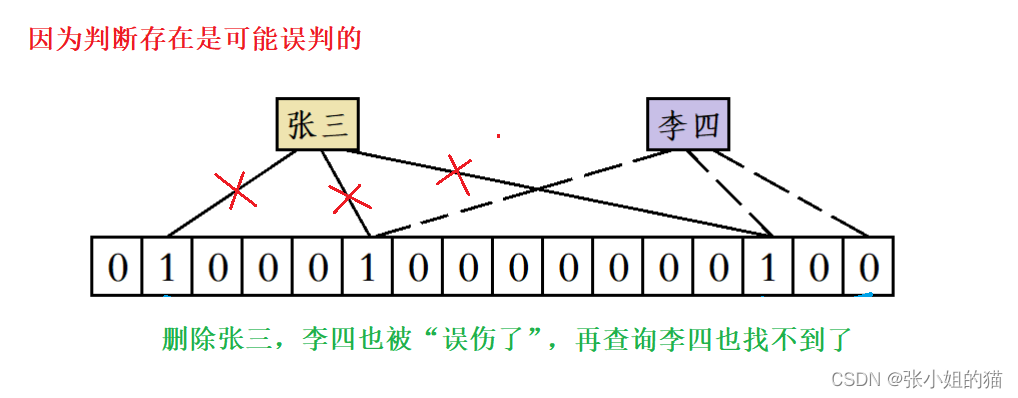
当然也不是完全没有办法的
- 我们只需要在每个比特位加一个计数器当存在插入操作时在计数器里面进行
++
操作删除后对该位置进行--即可
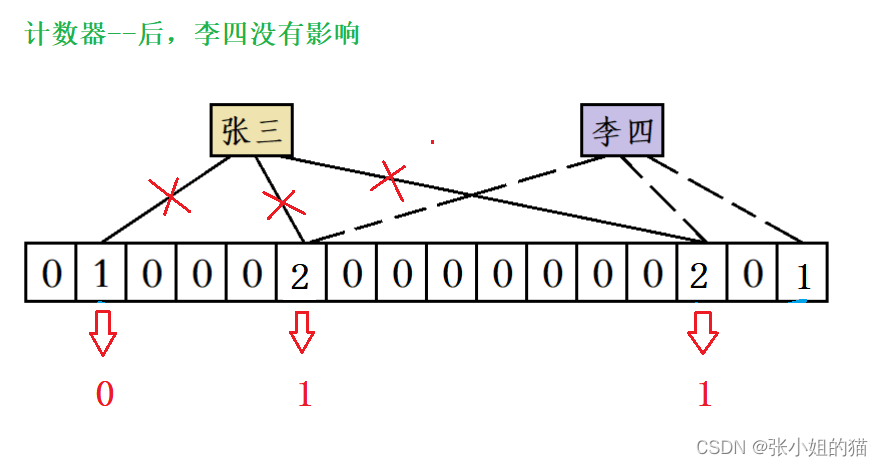
其实过滤器的本来目的就是为了提高效率和节省空间在每个比特位增加额外的计数器更是让空间开销飙升到本身的好几倍空间消耗更多了优势削弱了
💥优劣分析
优势相当亮眼
- 不受数据量大小影响增加和查询元素的时间复杂度为
O(K)K为哈希函数的个数一般比较小 - 布隆过滤器不需要存储元素本身对保密要求比较严格的场合有很大优势
- 在能够承受一定的误判时布隆过滤器比其他数据结构有着很大的空间优势
- 数据量很大时也可以表示全集其他数据结构不能
- 使用同一组哈希函数的布隆过滤器可以进行交、并、差运算
缺点也有
- 有误判率存在假阳性即不能准确判断元素是否在集合中补救方法再自建一个白名单存储可能会误判的数据
- 不能获取元素本身
- 一般情况下不能从布隆过滤器中删除元素
🔥哈希切割面试题
1️⃣给两个文件分别有100亿个query我们只有1G的内存如何找到两个文件的交集精确算法
- 首先我们分析大小每个query 30个字节 100亿个query需要3000亿个byte也就是300G的空间
1G == 10亿字节 - 重点相同的query是一定进入相同编号的小文件再对这些文件放进内存的两个set中编号相同的Ai和Bi小文件找交集即可
- 小文件不是平均分的有些进的多有些少如果某个小文件过大则要递归调用另一个哈希函数
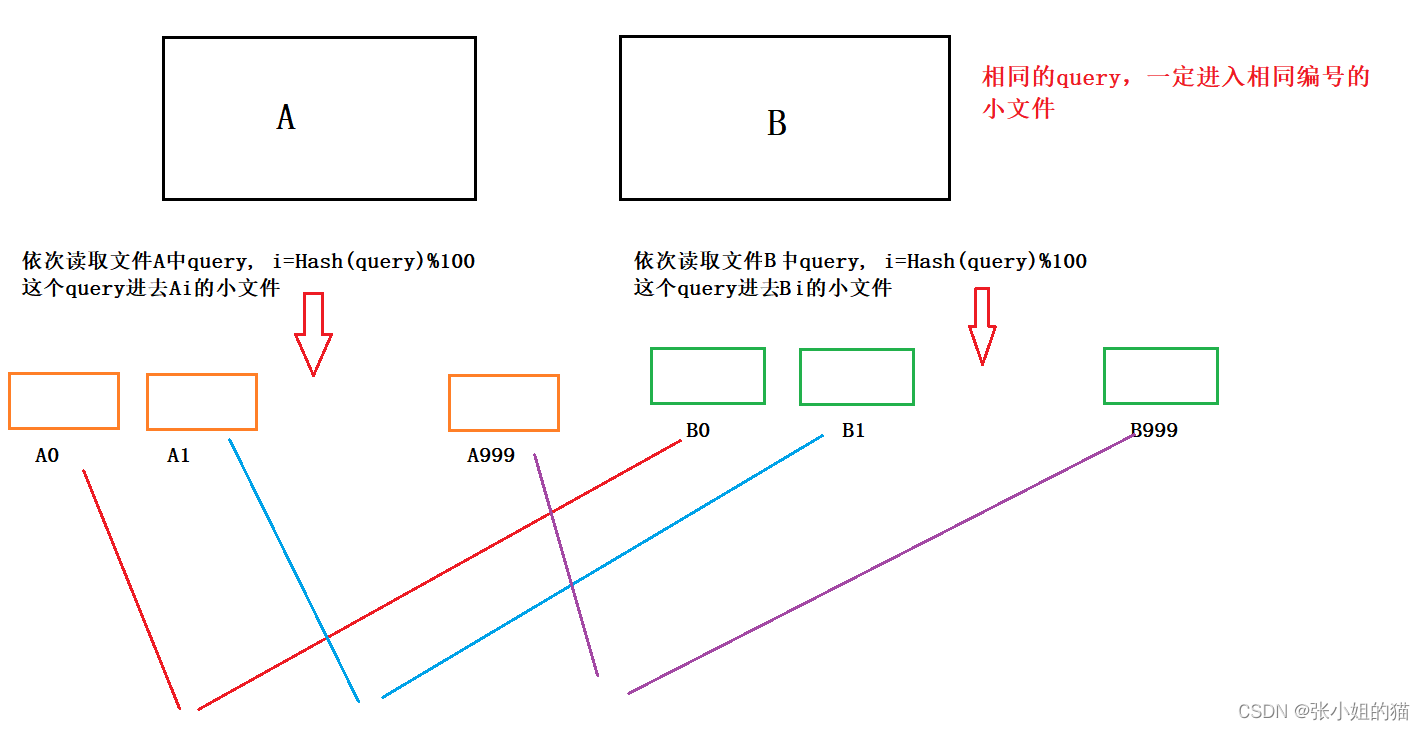
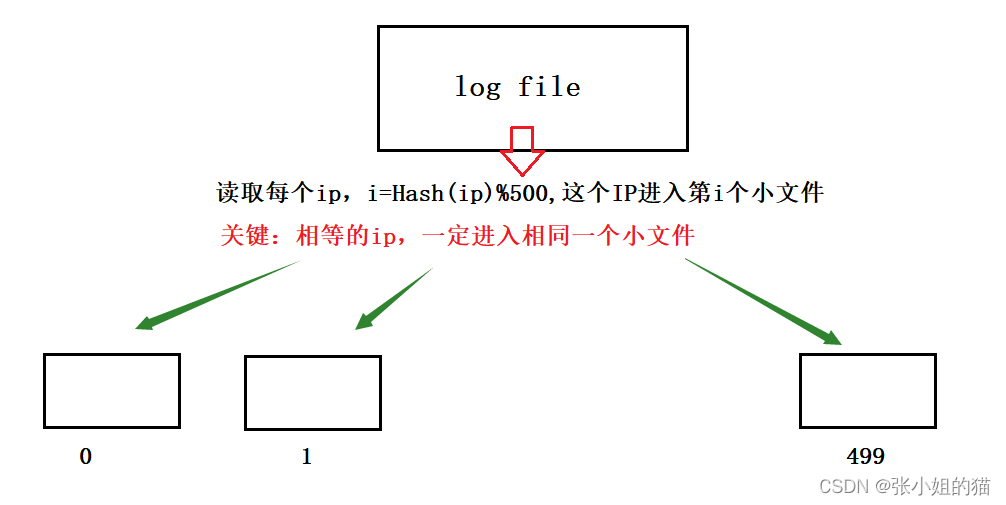
2️⃣给超过100G大小的log filelog中存着IP地址设计算法找出出现次数最多的IP地址如何找到top K 的IP
- 相等的
ip一定会进入相同的小文件 - 依次使用
map<stringint>对每个小文件统计次数 - topK建一个K个值为<ip, count>的小堆
📢写在最后
女拳什么时候爬


