【机器学习】聚类算法（理论）

阿里云国内75折回扣微信号：monov8

阿里云国际，腾讯云国际，低至75折。AWS 93折免费开户实名账号代冲值优惠多多微信号：monov8 飞机：@monov6

聚类算法理论

一、概论

聚类分析即聚类Clustering是指在一大推数据中采用某种方式或准则来将一些具有相同或相似性质和特征的数据划分为一类。聚类是无监督学习的典型算法相较于有监督学习由于聚类针对的大多是无标签数据因此对于最终构建的模型而言在进行模型评估时会比较麻烦。同时在对算法进行调参时也会因为这种不确定性而稍带困难。

Alt

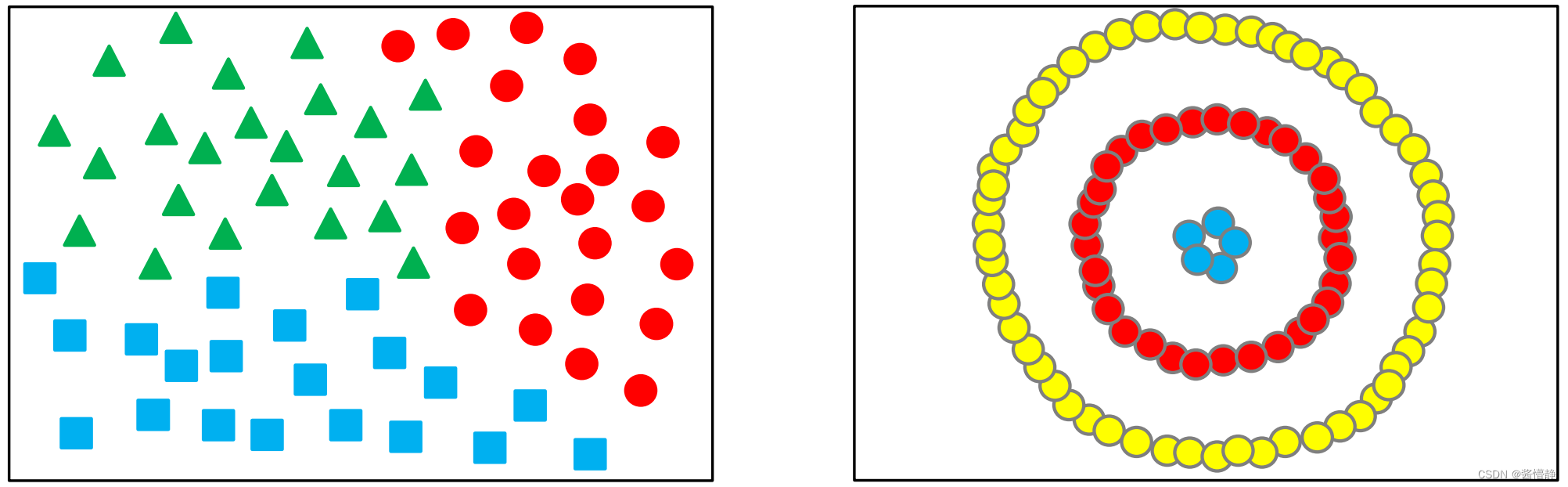
1、聚类算法的分类

聚类算法的分类有

划分法
划分法(Partitioning Methods)给定一个有N个元组或者纪录的数据集分裂法将构造K个分组每一个分组就代表一个聚类K小于N。而且这K个分组满足下列条件
1每一个分组至少包含一个数据纪录
2每一个数据纪录属于且仅属于一个分组注意这个要求在某些模糊聚类算法中可以放宽
层次法
层次法(Hierarchical Methods)这种方法对给定的数据集进行层次似的分解直到某种条件满足为止。具体又可分为“自底向上”和“自顶向下”两种方案。例如在“自底向上”方案中初始时每一个数据纪录都组成一个单独的组在接下来的迭代中它把那些相互邻近的组合并成一个组直到所有的记录组成一个分组或者某个条件满足为止。
密度算法
基于密度的方法(Density-Based Methods)基于密度的方法与其它方法的一个根本区别是它不是基于各种各样的距离的而是基于密度的。这样就能克服基于距离的算法只能发现“类圆形”的聚类的缺点。
图论聚类法
图论聚类方法解决的第一步是建立与问题相适应的图图的节点对应于被分析数据的最小单元图的边或弧对应于最小处理单元数据之间的相似性度量。因此每一个最小处理单元数据之间都会有一个度量表达这就确保了数据的局部特性比较易于处理。图论聚类法是以样本数据的局域连接特征作为聚类的主要信息源因而其主要优点是易于处理局部数据的特性。
网格算法
基于网格的方法(Grid-Based Methods)这种方法首先将数据空间划分成为有限个单元cell的网格结构所有的处理都是以单个的单元为对象的。这么处理的一个突出的优点就是处理速度很快通常这是与目标数据库中记录的个数无关的它只与把数据空间分为多少个单元有关。
代表算法有STING算法、CLIQUE算法、WAVE-CLUSTER算法
模型算法
基于模型的方法(Model-Based Methods)基于模型的方法给每一个聚类假定一个模型然后去寻找能够很好的满足这个模型的数据集。这样一个模型可能是数据点在空间中的密度分布函数或者其它。它的一个潜在的假定就是目标数据集是由一系列的概率分布所决定的。
通常有两种尝试方向基于统计、基于神经网络。

2、欧氏空间的引入

世间万物皆为混沌。为此人类世界经历了原始社会、奴隶社会、封建社会、资本主义社会到共产主义社会这是人类社会从低级到高级的发展过程。但从哲学的角度看来这实际上是一种从无序到有序的过程。人类社会如此数学亦是如此。
数字的无穷尽给它的使用带来了极大不便为此在一维空间建立了“数轴”以将这些数字按序列在一条直线上既便于比较也便于查找与定位如𝑥。一维空间最经典的用例莫过于尺子用以测量长度。但是地图的出现让人们陷入苦恼要如何精准地定位一个人的位置呢“坐标轴”似乎是一个可行的方案通过在二维平面中额外增加一条与一维空间中的数轴所垂直的纵向数轴便能建立一个能海纳百川的空间此时可用 (𝑥, 𝑦) 定位任意位置。二维空间最典型的用例莫过于用于进行全球定位的经纬度。在建筑、设计类软件中处理目标更多的是立体图形此时二维空间便显得余力不足。很自然地想到可采取从一维到二维的相同提升方式即添加一条与二维平面相垂直的数轴这样一来就能构建一个涵盖三维空间全部位置的坐标轴以达到从二维空间到三维空间的提升此时可用 (𝑥, 𝑦, 𝑧) 定位任意位置。
Alt

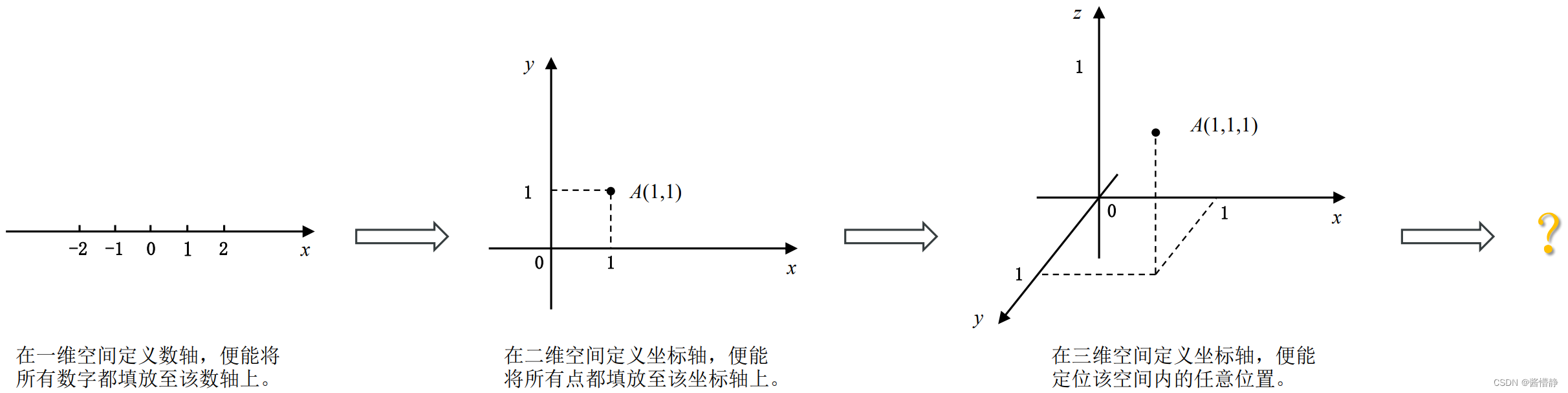
现在让我们回忆下不同空间中与距离相关的一些定义

在一维空间两个点 𝑥_𝑎, 𝑥_𝑏 之间的距离可以用 $distance(a,b)=\sqrt{(x_a-x_b)^2}=|x_a-x_b|$ 来表示
在二维空间两个点 𝐴(𝑥_𝑎, 𝑦_𝑎) , 𝐵(𝑥_𝑏, 𝑦_𝑏) 之间的距离可以用 $distance(a,b)=\sqrt{(x_a-x_b)^2+(y_a-y_b)^2}$ 来表示
在三维空间两个点 𝐴(𝑥_𝑎, 𝑦_𝑎, 𝑧_𝑎) , 𝐵(𝑥_𝑏, 𝑦_𝑏, 𝑧_𝑏) 之间的距离可以用 $distance(a,b)=\sqrt{(x_a-x_b)^2+(y_a-y_b)^2+(z_a-z_b)^2}$ 来表示

有关内积的定义

在一维空间两数 𝑥_𝑎, 𝑥_𝑏 之积为 Mul(𝑎, 𝑏) = 𝑥_𝑎𝑥_𝑏
在二维空间两个点 𝐴(𝑥_𝑎, 𝑦_𝑎) , 𝐵(𝑥_𝑏, 𝑦_𝑏) 之间的内积可以用 Mul(𝐴, 𝐵) = 𝑥_𝑎𝑥_𝑏 + 𝑦_𝑎𝑦_𝑏来表示
在三维空间两个点 𝐴(𝑥_𝑎, 𝑦_𝑎, 𝑧_𝑎) , 𝐵(𝑥_𝑏, 𝑦_𝑏, 𝑧_𝑏) 之间的内积可以用 Mul(𝐴, 𝐵) = 𝑥_𝑎𝑥_𝑏 + 𝑦_𝑎𝑦_𝑏 + 𝑧_𝑎𝑧_𝑏 来表示。

Alt

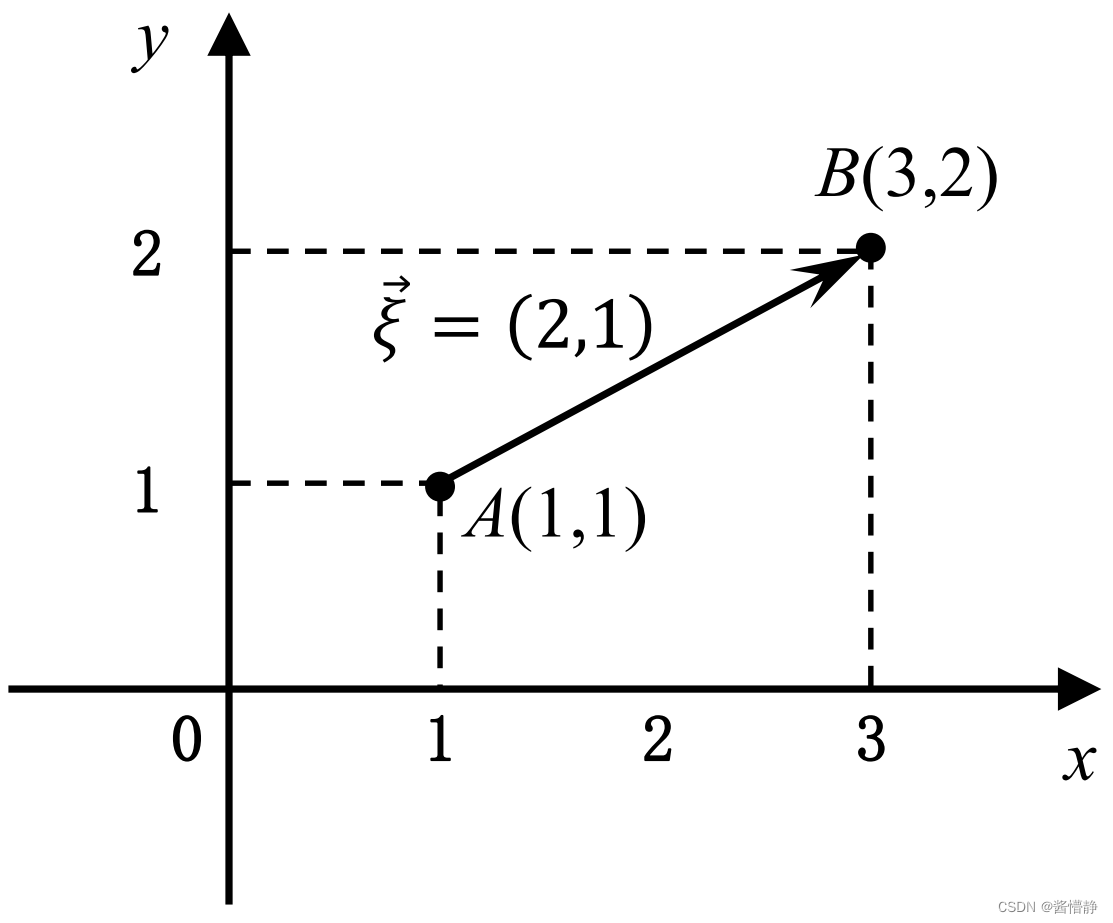
在二维及以上空间基于两点 𝑋(𝑥₁, 𝑥₂, … , 𝑥_𝑛) , 𝑌(𝑦₁, 𝑦₂, … , 𝑦_𝑛) 可定义一个具有方向的指标称其为向量则可得到
$\vec{\xi} = \{ a_1, a_2, … ,a_n \} = \{ x_1, x_2, …, x_n \} - \{ y_1, y_2, …, y_n \} = \{ x_1 - y_1, x_2 - y_2, …, x_n - y_n \}$
对于高维空间定义两向量的内积为 $\vec{\xi}·\vec{\eta}=\sum_{i=1}^na_ib_i=a_1b_1+a_2b_2+…+a_nb_n$ 这个内积和两点之间的内积算法是一致的。
有时候我们需要通过两个向量之间的夹角来判断与其相关的一些性质为此定义了方向余弦其定义为
$\theta=\frac{\vec{\xi}·\vec{\eta}}{|\vec{\xi}|·|\vec{\eta}|}$
以上就是在低维空间一维、二维、三维构建的一系列“秩序”以帮助我们理解与使用而高维空间却因它的抽象性显得较有难度。但是依然可采取与前面的相同的思路来进行拓展。此时若将在低纬空间总结的有关距离、内积、角相关的定理推广至有限的更高维空间那这些符合定义的空间则被统称为欧几里得空间亦即欧式空间Euclidean Space。

二、K-Means算法

1、算法思路

K-Means 算法是一种典型的基于划分的聚类算法它的核心思想是若将指定数据集的特征投影至 n 维欧氏空间则数据之间的相似性应当与这些数据的欧氏距离成反比。说简单点就是越相似的数据彼此之间离得越近。
其算法流程如下首先从数据集中随机选取 𝑘 个初始聚类中心 𝐶_𝑗 (1 ≤ 𝑗 ≤ 𝑘) 接下来对每个其余数据对象均计算出该数据对象与 𝑘 个聚类中心的的欧式距离并将离目标数据对象最近的聚类中心 𝐶_𝑥 作为该数据对象所属的类别。经过这样一次迭代就完成了一次 K-Means 聚类。接着计算每个簇中数据对象的平均值作为新的聚类中心进行下一次迭代直到聚类中心不再变化或达到最大的迭代次数时停止。

Alt

上图给出了 K-Means 算法的执行流程通过观察显然可将该数据集划分为 2 类因此取 k = 2

(a) 算法开始将指定数据集的特征投影至 n 维欧氏空间
(b) 随机选取 k = 2 个初始聚类中心
(c) 对任意数据 x^(𝑖) 算出其与 k 个聚类中心的欧式距离取其中距离最近的那个类簇作为数据 x^(𝑖) 的所属类别第一次 k-means
(d) 基于新的类簇分布算出每个簇中数据对象的平均值作为新的聚类中心
(e) 对任意数据 x^(𝑖) 算出其与 k 个聚类中心的欧式距离取其中距离最近的那个类簇作为数据 x^(𝑖) 的所属类别第二次 k-means
(f) 基于新的类簇分布算出每个簇中数据对象的平均值作为新的聚类中心

(f) 之后算法将执行第三次 k-means接着当再次计算新的类簇中心时会发现类簇中心不再发生变化或变化
范围很小此时算法停止并返回最终的分类结果。

总的来看K-Means 算法需要预先指定初始类簇个数和聚类中心然后再按照样本与类簇中心的距离进行归类与迭代更新。在迭代过程中 K-Means 算法会不断降低各类簇的误差平方和SSESum of Squared ErrorSSE当SSE不再变化或目标函数收敛时聚类结束得到最终结果。下面给出 K-Means 算法计算某个数据对象 𝑥^(𝑖) 与某类簇中心 𝐶_𝑗 的欧氏距离公式
$\left( x^{(i)},C_j \right)=\sqrt{\sum_{t-1}^m{\left( x_t^{(i)}-C_{jt} \right)^2}}$
其中 $x_t^{(i)}$ 为第 𝑖 个数据对象在第 𝑡 个特征上的取值𝐶_{𝑗𝑡} 为第 𝑗 个数据对象在第 𝑡 个特征上的取值。
整个数据集的误差平方和 SSE 计算公式为SSE的大小衡量了聚类结果的好坏
$SSE=\sum_{j=1}^k\sum_{x^{(i)}∈C_j} \left( distance( x^{(i)},C_j) \right)^2$

2、算法总结

自此可总结出 K-Means 算法的步骤

① 随机选择 k 个样本作为初始簇类的均值向量
② 将每个样本数据划分给离它距离最近的簇
③ 根据每个样本所属的簇更新簇类的均值向量
④ 重复 ②③ 步当达到设置的迭代次数或类簇的均值向量不再改变时模型构建完成输出聚类算法结果。

K-Means 算法非常简单且使用广泛但是主要存在以下四个缺陷

K 值需要人为给定属于预先知识大多情况下 K 值的估计非常困难。对于“可以确定 K 值不会太大但不明确具体取值”的场景可以进行多次迭代运算然后找出 SSE 值最小的的 K 值作为最终的类簇个数
K-Means 算法对初始选取的聚类中心点是敏感的不同的随机种子点得到的聚类结果完全不同
该算法并不适合所有的数据类型。它不能处理非球形簇、不同尺寸和不同密度的簇
易陷入局部最优解。

Alt
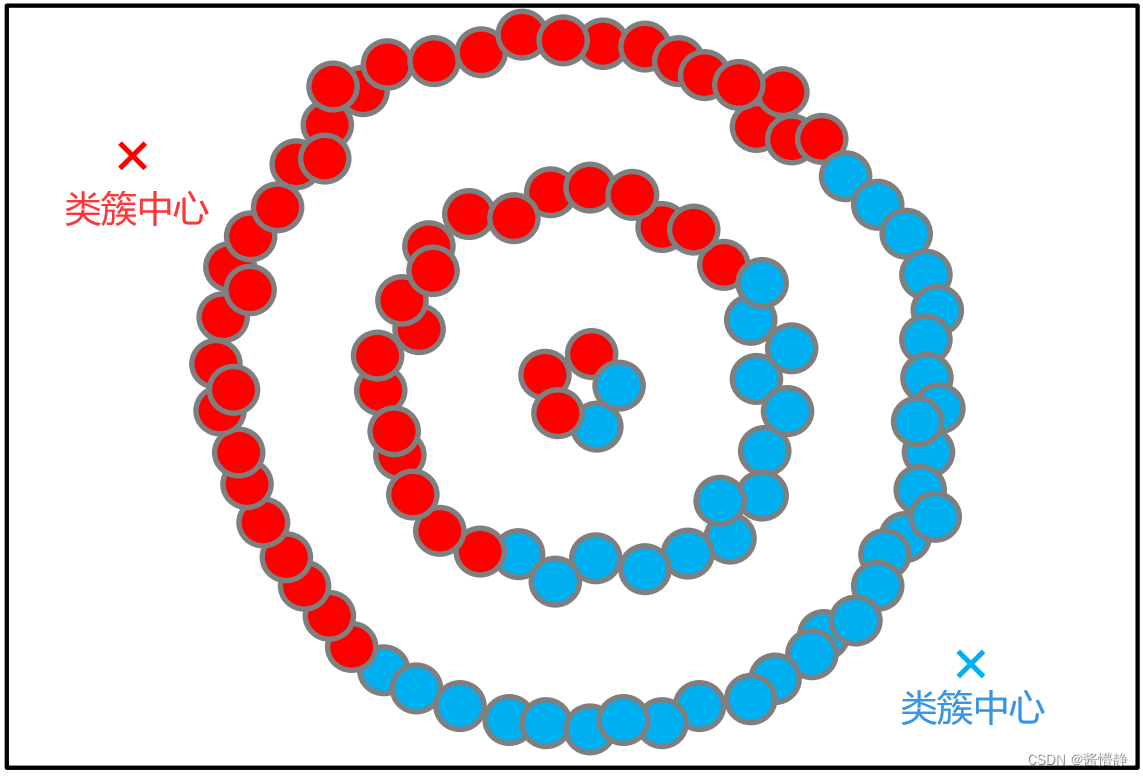
从上图不难看出K-Means算法对于环形簇的分类效果非常糟糕

三、DBSCAN算法

1、相关概念

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)翻译是“基于密度的带噪声聚类算法”DBSCAN 将簇定义为“密度相连的点的最大集合”它把具有足够高密度的区域划分为簇能在带噪声的数据中发现任意形状的类簇。为理解 DBSCAN 的算法原理下面先介绍一些相关概念假设样本集为 𝐷 = {𝑥⁽¹⁾, 𝑥⁽²⁾, … , 𝑥^(𝑛)}

𝝐 − 领域对于某个样本点 𝑥^(𝑗) ∈ 𝐷其 𝜖 − 领域包含样本集 D 中与 𝑥^(𝑗) 的距离不大于 𝜖 的子样本集。即𝑁_𝜖 (𝑥^(𝑗))= { 𝑥^(𝑖) ∈ 𝐷 | 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒(𝑥^(𝑖), 𝑥^(𝑗)) ≤ 𝜖} 用 | 𝑁_𝜖(𝑥^(𝑗)) |表示该子样本集中的样本点个数。注上述距离的计算通常采用欧式距离、曼哈顿距离等。
核心对象对于任意样本 𝑥^(𝑗) ∈ 𝐷如果它的 𝜖 − 领域中包含的样本点个数至少包含 𝑀𝑖𝑛𝑃𝑜𝑖𝑛𝑡𝑠 个样本即 | 𝑁_𝜖(𝑥^(𝑗)) | ≥ 𝑀𝑖𝑛𝑃𝑜𝑖𝑛𝑡𝑠则称 𝑥^(𝑗) 为一个核心对象。
密度直达如果 𝑥^(𝑖) 位于 𝑥^(𝑗) 的 𝜖 − 邻域中且 𝑥^(𝑗) 是核心对象则称 𝑥^(𝑖) 由 𝑥^(𝑗) 密度直达。反之不一定成立即此时不能说 𝑥^(𝑗) 由 𝑥^(𝑖) 密度直达, 除非 𝑥^(𝑖) 也是核心对象即密度直达不具有对称性。
密度可达对于 𝑥^(𝑖) 和 𝑥^(𝑗) 如果存在样本序列 𝑝⁽¹⁾, 𝑝⁽²⁾, … , 𝑝^(𝑡)使得任意 𝑝^(𝑘) 均可由 𝑝^{(𝑘−1)} 密度直达其中 2 ≤ 𝑘 ≤ 𝑡且 𝑥^(𝑗)= 𝑝⁽¹⁾, 𝑥^(𝑖)= 𝑝^(𝑡)则称 𝑥^(𝑖) 由 𝑥^(𝑗) 密度可达。也就是说密度可达具有传递性。此时序列中的传递样本 𝑝⁽¹⁾, 𝑝⁽²⁾, … , 𝑝^{(𝑡-1)} 均为核心对象因为只有核心对象才能使其他样本密度直达。同时由密度直达不具有对称性可知密度可达也不具有对称性。
密度相连对于 𝑥^(𝑖) 和 𝑥^(𝑗)如果存在核心对象样本 𝑥^(𝑡) 使 𝑥^(𝑖) 和 𝑥^(𝑗) 均由 𝑥^(𝑡) 密度可达则称 𝑥^(𝑖) 和 𝑥^(𝑗) 密度相连。密度相连关系满足对称性。

基于下图可以很容易理解上述定义图中 𝑀𝑖𝑛𝑃𝑜𝑖𝑛𝑡𝑠 = 4红色的点都是核心对象因为其 𝜖 − 邻域至少有 4 个样本。黑色的样本是非核心对象。所有核心对象密度直达的样本都在以红色核心对象为中心的圆内如果不在圆内则不能密度直达。图中用蓝色箭头连起来的核心对象组成了密度可达的样本序列此序列是一个簇集。在这些密度可达的样本序列的 𝜖 − 邻域内所有的样本相互都是密度相连的 (注意此图中有两个簇集)。

Alt

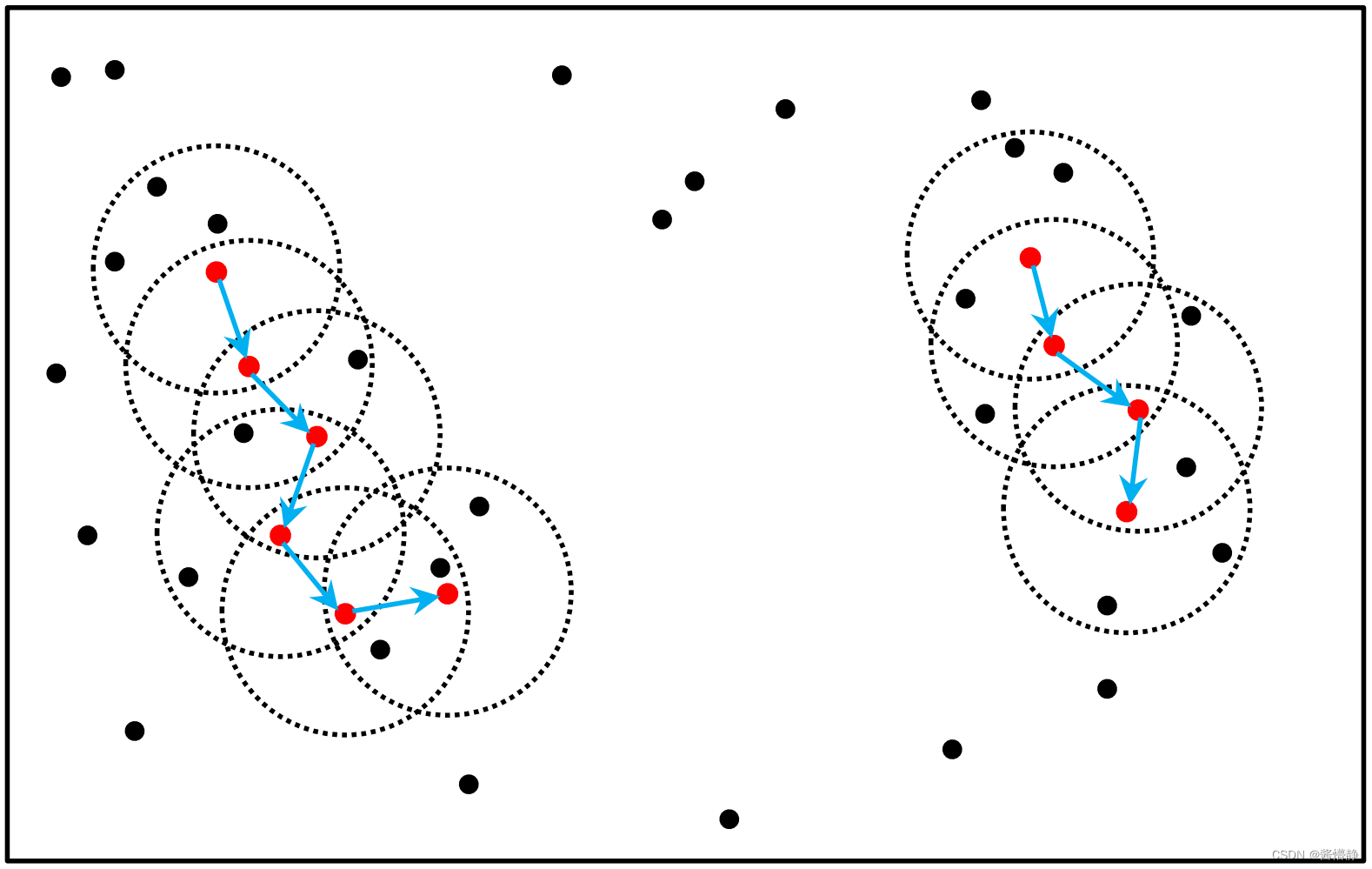
2、算法思路

DBSCAN 的聚类定义很简单由密度可达关系导出最大密度相连的样本集合即为我们最终聚类的一个簇。簇里面可以有一个或者多个核心对象。如果只有一个核心对象则簇里其他的非核心对象样本都在这个核心对象的 𝜖 − 邻域里如果有多个核心对象则簇里的任意一个核心对象的 𝜖 − 邻域中一定至少有一个其他核心对象否则这两个核心对象无法密度可达。这些核心对象的 𝜖 − 邻域里的所有样本集合就组成了一个DBSCAN 聚类簇。

现在我们讨论下如何根据 DBSCAN 的聚类定义来对数据集进行聚类。首先在样本集中选出所有的核心对象并构成一个集合 𝛺然后在 𝛺 中任意选择一个数据点作为根并标记该数据点作为一个新类簇接下来寻找所有这个核心对象能够密度可达的样本集合并将这个集合中的所有点都归类到根所在类簇中这便找到了一个类这样得到的所有数据点肯定都是密度相连的。之后不断按这样的方式寻找新类簇直到集合 𝛺 中的所有核心对象都有类别为止。最终剩余未被归类的数据点即被称为“噪声点”或“离群点”。因此DBSCAN 算法也可用于识
别噪声点。

基于以上讨论下面给出 DBSCAN 算法的具体流程
① 初始化核心对象集合 𝛺 = ∅ 待查子集合 𝛹 = ∅ 初始化类簇个数 𝑘 = 0
② 遍历样本集 𝐷 的元素如果是核心对象则将其加入到核心对象集合 𝛺 中
③ 接下来遍历核心对象集 𝛺
④ 若核心对象集 𝛺 中所有元素都已被访问则算法结束否则转入步骤 ⑤
⑤ 在核心对象集 𝛺 中随机选择一个未被访问的核心对象 𝛼。首先将其标记为已访问然后将 𝛼 所属类别标记为 𝑘最后再将 𝛼 的 𝜖 − 邻域中的所有未被访问数据存放到待查子集合 𝛹 中
⑥ 如果待查子集合 𝛹 = ∅则当前类簇 𝐶_𝑘 生成完毕令 𝑘 = 𝑘 + 1并跳转到 ③。否则从待查子集合 𝛹 中选出一个数据点 𝜓 。首先将其标记为已访问并标记所属类别为 𝑘然后判断 𝜓 是否为核心对象如果是则将 𝜓 包含的未被访问的数据点加入到待查子集合 𝛹 中并跳转到 ⑥。

Alt

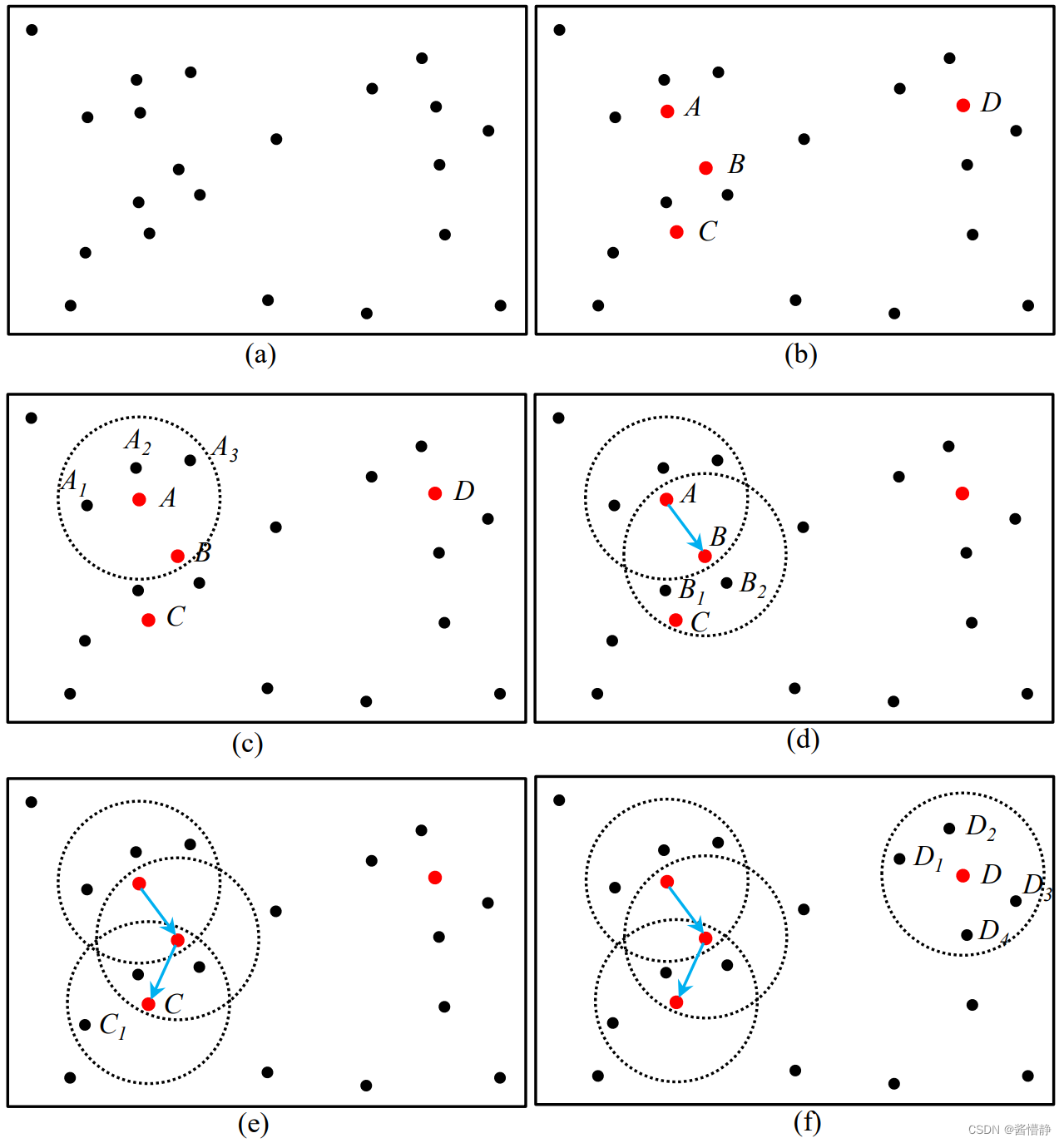
上图展示了 DBSCAN 算法的执行流程图中 𝑀𝑖𝑛𝑃𝑜𝑖𝑛𝑡𝑠=4

(a) 算法开始将指定数据集的特征投影至 𝑛 维欧氏空间并构建核心对象集 𝛺 = ∅ 、待查子集 𝛹 = ∅ 、令初始类簇个数 𝑘 = 0。
(b) 遍历样本数据集选出所有的核心对象并存放至核心对象集合 𝛺 中即有 𝛺 = {𝐴,𝐵,𝐶,𝐷}。
(c) 接下来遍历核心对象集 𝛺直到所有的核心对象都被访问过。开始时可任意选出一个核心对象如 𝐴 。首先将其标记为已访问然后将𝐴 所属类别标记为 𝑘 = 0 最后再将 𝐴 的 𝜖 − 邻域中的所有未被访问数据存放进待查子集合 𝛹 中即有 𝛹 = {𝐴₁,𝐴₂,𝐴₃,𝐵}。
接着对 𝛹 进行遍历直到 𝛹 为空。第一次从 𝛹 中取出数据点 𝐴₁ 首先将𝐴₁ 标记为已访问然后将 𝐴₁ 归类至 𝑘=0最后判断 𝐴₁ 不是核心对象不做处理第二次从𝛹 中取出数据点 𝐴₂ 首先将 𝐴₂ 标记为已访问然后将 𝐴₂ 归类至 𝑘 = 0最后判断 𝐴₂ 不是核心对象不做处理第三次从 𝛹 中取出数据点 𝐴₃首先将 𝐴₃ 标记为已访问然后将 𝐴₃ 归类至 𝑘 = 0最后判断 𝐴₃ 不是核心对象不做处理第四次从 𝛹 中取出数据点 𝐵 首先将 𝐵 标记为已访问然后将 𝐵 归类至 𝑘 = 0最后判断𝐵 是核心对象因此将
𝐵 包含的未被访问的数据点加入到待查子集合 𝛹 中此时 𝛹 = {𝐵₁,𝐵₂,𝐶}。如图(d)所示。
(d) 𝛹 不空继续对 𝛹 进行遍历直到 𝛹 为空。第一次从 𝛹 中取出数据点 𝐵₁首先将 𝐵₁ 标记为已访问然后将 𝐵₁ 归类至 𝑘=0最后判断 𝐵₁ 不是核心对象不做处理第二次从 𝛹 中取出数据点 𝐵₂ 首先将 𝐵₂ 标记为已访问然后将 𝐵₂ 归类至 𝑘 = 0 最后判断 𝐵₂ 不是核心对象不做处理第三次从 𝛹 中取出数据点 𝐶 首先将 𝐶 标记为已访问然后将 𝐶 归类至 𝑘 = 0 最后判断 𝐶 是核心对象因此将 𝐶 包含的未被访问的数据点加入到待查子集合 𝛹 中此时 𝛹 = {𝐶₁} 如图(e)所示。
(e) 𝛹 不空继续对 𝛹 进行遍历直到 𝛹 为空。第一次从 𝛹 中取出数据点 𝐶₁首先将 𝐶₁ 标记为已访问然后将 𝐶₁ 归类至 𝑘 = 0 最后判断 𝐶₁ 不是核心对象不做处理。此时待查子集 𝛹 = ∅表示当前类簇 𝐶₀ 已经生成完毕令 𝑘 = 𝑘+1 = 0+1 = 1开始寻找下一个类簇。即退至核心对象集合 𝛺 继续遍历 𝛺 以寻找尚未被访问过的核心对象。
(f) 𝛺 = {A,𝐵,𝐶,𝐷} 中A、𝐵、𝐶 均已被访问此时仅剩 𝐷 将其选出。首先将其标记为已访问然后将𝐷 所属类别标记为 𝑘 = 1最后再将 𝐷 的 𝜖 − 邻域中的所有未被访问数据存放进待查子集合 𝛹 中即有 𝛹 = {𝐷₁,𝐷₂,𝐷₃,𝐷₄}。
接着对 𝛹 进行遍历直到 𝛹 为空。第一次从 𝛹 中取出数据点 𝐷₁首先将 𝐷₁ 标记为已访问然后将 𝐷₁ 归类至 𝑘 = 1最后判断 𝐷₁ 不是核心对象不做处理第二次从 𝛹 中取出数据点 𝐷₂首先将 𝐷₂ 标记为已访问然后将 𝐷₂ 归类至 𝑘 = 1最后判断 𝐷₂ 不是核心对象不做处理第三次从 𝛹 中取出数据点 𝐷₃ 首先将 𝐷₃ 标记为已访问然后将 𝐷₃ 归类至 𝑘 = 1最后判断𝐷₃ 不是核心对不做处理第四次从 𝛹 中取出数据点 𝐷₄首先将 𝐷₄ 标记为已访问然后将 𝐷₄ 归类至 𝑘 = 1最后判断 𝐷₄ 不是核心对象不做处理。
此时待查子集 𝛹 = ∅表示当前类簇 𝐶₁ 已经生成完毕令 𝑘 = 𝑘+1 = 1+1 = 2开始寻找下一个类簇。即退至核心对象集合 𝛺 继续遍历 𝛺 以寻找尚未被访问过的核心对象。
𝛺 = {𝐴,𝐵,𝐶,𝐷} 中所有元素均已被访问退出算法。

输出所有类簇𝐶₀、𝐶₁。

3、算法总结

DBSCAN 算法不是一个完全稳定的算法。例如某些样本可能到两个核心对象的距离都小于 𝜖但是由于这两个核心对象不是密度直达且又不属于同一个类簇那么如果界定这些样本的类别呢此时DBSCAN 通常会采用先来后到的准则即在算法执行过程中这些样本先被归到哪一类则最终就隶属于那一类。所以同一数据集在 DBSCAN 的执行过程中某些样本最终的归类并不一定严格一致。

DBSCAN 的主要优点