什么是背包问题

背包问题是有N件物品容量为V的背包

每个物品有两个属性体积价值分别用数组vw表示

第i件物品的体积为v[i]价值为w[i]

计算在背包装得下的情况下能装的最大价值是多少

根据不同的限制条件主要有以下三种背包问题

• 01背包
• 完全背包
• 多重背包

01背包

每件物品最多用一次

朴素做法

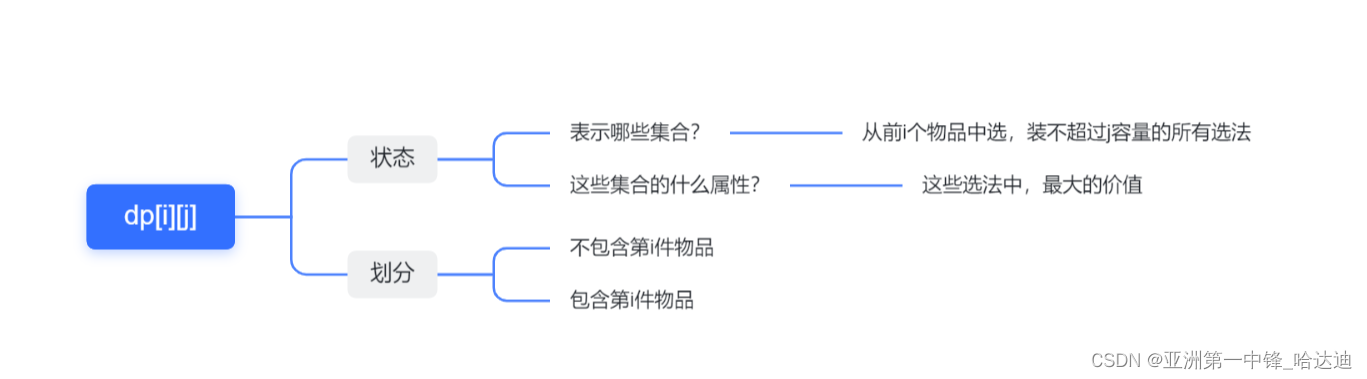
定义二维数组dpdp[i][j]表示

• 哪些集合从前i个物品中选装不超过j容量的所有选法
• 什么属性这些选法中最大的价值

根据dp数组的定义dp[N][V]就是最终要求解的答案

接下来看一个普遍的位置dp[i][j]其表示的集合可以划分为哪些集合

所有从前i个物品中选装不超过j容量的所有选法中可以被不重不漏地划分为

1. 不包含第i件物品
2. 包含第i件物品

dp[i][j] = max(前i件物品中选且不包含第i件物品的最大价值前i件物品中选且包含第i件物品的最大价值)

前i件物品中选且不包含第i件物品的最大价值和dp[i - 1][j]的定义是一样的

前i件物品中选且包含第i件物品的最大价值这种情况可以将所有的选法中第i件物品的价值提出来除了第i件物品的价值外还要加上在前i-1件物品中选容量不超过j - v[i]的最大价值这和dp[i - 1][j - v[i]]的定义一样

因此dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])

我们只要在计算dp[i][j]时保证其依赖的项已经计算过计算过程就是正确的

怎么保证之前的已经计算过呢按照如下的循环方式计算

public  static  int  bag01 ( int N, int V, int [] w, int []v) {  
    int [][] dp = new  int [N+ 1 ][V+ 1 ];  
    for ( int  i  =  1 ;i <= N;i++) {  
        for ( int  j  =  0 ;j <= V;j++) { 
            dp[i][j] = dp[i- 1 ][j];  
            if (j >= v[i]) { 
                dp[i][j] = Math. max (dp[i][j], dp[i- 1 ][j-v[i]] + w[i]); 
            } 
        } 
    }  
    return dp[N][V]; 
}

空间优化

可以发现在计算第i层时只用到了第i-1层这样可以用一个只有两层的数组滚动计算

进一步可以发现使用到的j要么是第i-1层的j要么是第i-1层j的左侧不是j左右两侧都依赖因此可以优化为只使用一层的数组

需要注意在计算每一层的数据时不能从左往右计算因为会将本层的数据覆盖掉本该是上一层的数据

需要从右往左计算

public  static  int bag01(int N,int V,int[] w,int []v) {
    int[] dp = new  int[V+1];
    for (int i = 1;i<=N;i++) {
        for (int j = V;j >= v[i];j--) {
            dp[j] = Math.max(dp[j], dp[j-v[i]] + w[i]);
        }
    }
    return dp[V];
}

完全背包

每件物品可以用无数多次

朴素做法

定义二维数组dpdp[i][j]表示

• 哪些集合从前i个物品中选装不超过j容量的所有选法
• 什么属性这些选法中价值的最大的价值

所有从前i个物品中选装不超过j容量的所有选法中可以被不重不漏地划分为

1. 第i个物品不选
2. 第i个物品选1个
3. 第i个物品选2个
4. …
5. 第i个物品选k个k * v[i] 需要小于等于j

即

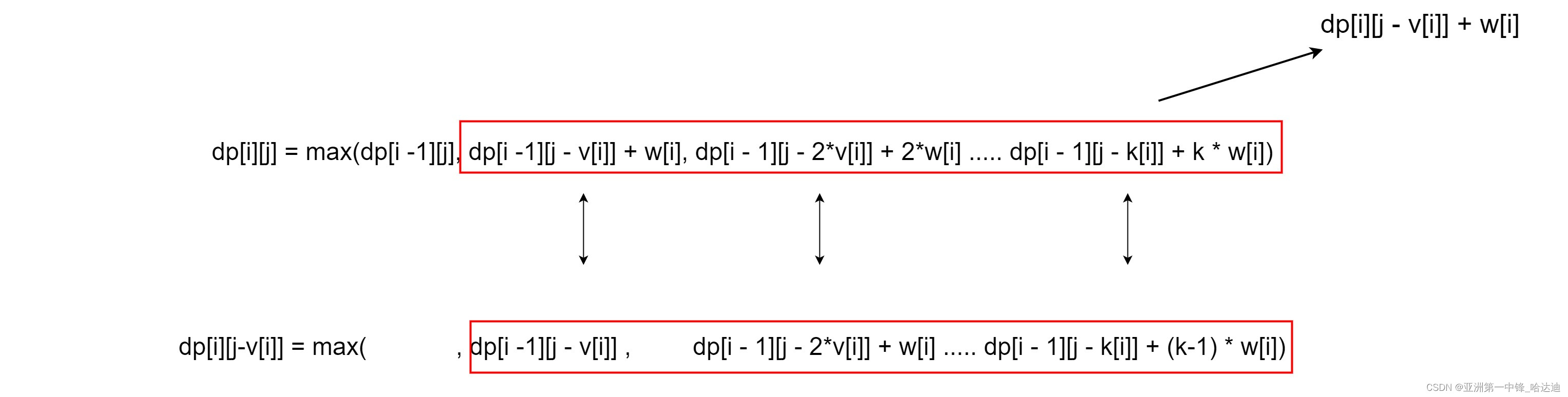
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i], dp[i - 1][j - 2*v[i]] + 2*w[i] ..... dp[i-1][j - k[i]] + k*w[i])

代码实现为

public  static  int bagComplete(int N,int V,int[] w,int []v) {
    int[][] dp = new  int[N+1][V+1];
    for (int i = 1;i<=N;i++) {
        for (int j = 0;j <= V;j++) {
            for (int k = 0;k * v[i] <= j;k++) {
                dp[i][j] = Math.max(dp[i][j], dp[i][j-k * v[i]] + k * w[i]);
            }
        }
    }
    return dp[N][V];
}

时间优化

上面的朴素做法在时间复杂度上是一个三重循环为O(N ^ 3)可以优化为O(N ^ 2)

我们列出dp[i][j]和dp[i][j - v[i]]的公式对比

可以发现dp[i][j]从第二项开始直到结束和dp[i][j - v[i]]的第一项直到结束十分相似

区别在于dp[i][j]的每一项比dp[i][j - v[i]]的每一项多了w[i]

那么dp[i][j]从第二项开始往后的最大值等于dp[i][j - v[i]]的值加上 w[i]再结合dp[i][j]的第一项得到

dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])

代码可以优化为

public  static  int bagComplete(int N,int V,int[] w,int []v) {
    int[][] dp = new  int[N+1][V+1];
    for (int i = 1;i<=N;i++) {
        for (int j = 0;j <= V;j++) {
            dp[i][j] = dp[i-1][j];
            if (j >= v[i]) {
                dp[i][j] = Math.max(dp[i][j], dp[i][j - v[i]] + w[i]);
            }
        }
    }
    return dp[N][V];
}

空间优化

同样完全背包也可以优化为只用一层数组

由于使用的上一层j位置的值和当前层j左边位置的值因此需要在每一层从左往右遍历这点和01背包不一样

public  static  int bagComplete02(int N,int V,int[] w,int []v) {
    int[] dp = new  int[V+1];
    for (int i = 1;i<=N;i++) {
        for (int j = v[i];j <= V;j++) {
            dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
        }
    }
    return dp[V];
}

01背包和多重背包的区别

这两个问题的最终版代码十分相似唯一的区别就是

• 01背包每一层从右往左推
• 完全背包每一层从左往右推

多重背包

每件物品能用的次数由一个数组c表示第i件物品能用c[i]次

朴素做法

定义二维数组dpdp[i][j]表示

• 哪些集合从前i个物品中选装不超过j容量的所有选法
• 什么属性这些选法中价值的最大的价值

所有从前i个物品中选装不超过j容量的所有选法中可以被不重不漏地划分为

1. 第i个物品不选
2. 第i个物品选1个
3. 第i个物品选2个
4. …
5. 第i个物品选k个k * v[i] 需要小于等于j且k小于等于c[i]

代码如下

public  static  int bagMulti(int N,int V,int[] w,int []v, int[] c) {
    int[][] dp = new  int[N+1][V+1];
    for (int i = 1;i<=N;i++) {
        for (int j = 0;j <= V;j++) {
            for (int k = 0;k * v[i] <= j && k <= c[i]; k++) {
                dp[i][j] = Math.max(dp[i][j], dp[i][j - k * v[i]] + k * w[i]);
            }
        }
    }
    return dp[N][V];
}

时间优化

朴素做法的时间复杂度为O(N^3)可否像完全背包那样优化呢

我们列举dp[i][j]和 dp[i][j - v[i]]的每一项

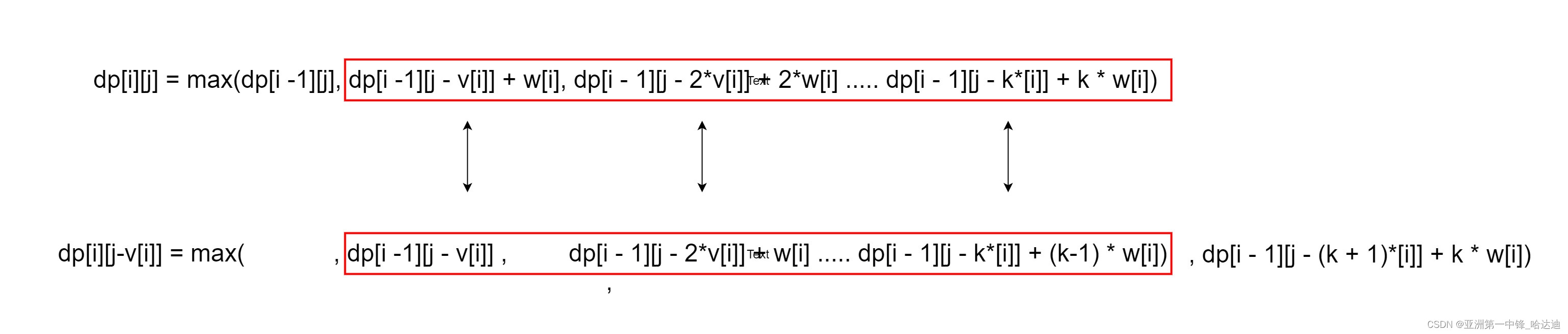
我们需要dp[i][j - v[i]]中除了最后一项以外其他项的最大值但无法根据整体的最大值推算局部的最大值

因此无法像完全背包那样优化

二进制优化

例如当s[i] = 19

我们将其打包为分别有1,2,4,8,4个第i件物品的组在这些组中用01背包的方式计算最大价值
打包规则为另k=0从1,2,4,8,16一直往后累加直到s[i] - k小于k为止将s[i] - k作为最后一组打包

例如s[i] = 100时打包成以下几组 1,2,4,8,16,32,37

即在5个组中选每个物品最多选1次

这个做法和第i件物品最多选19次是否等价呢

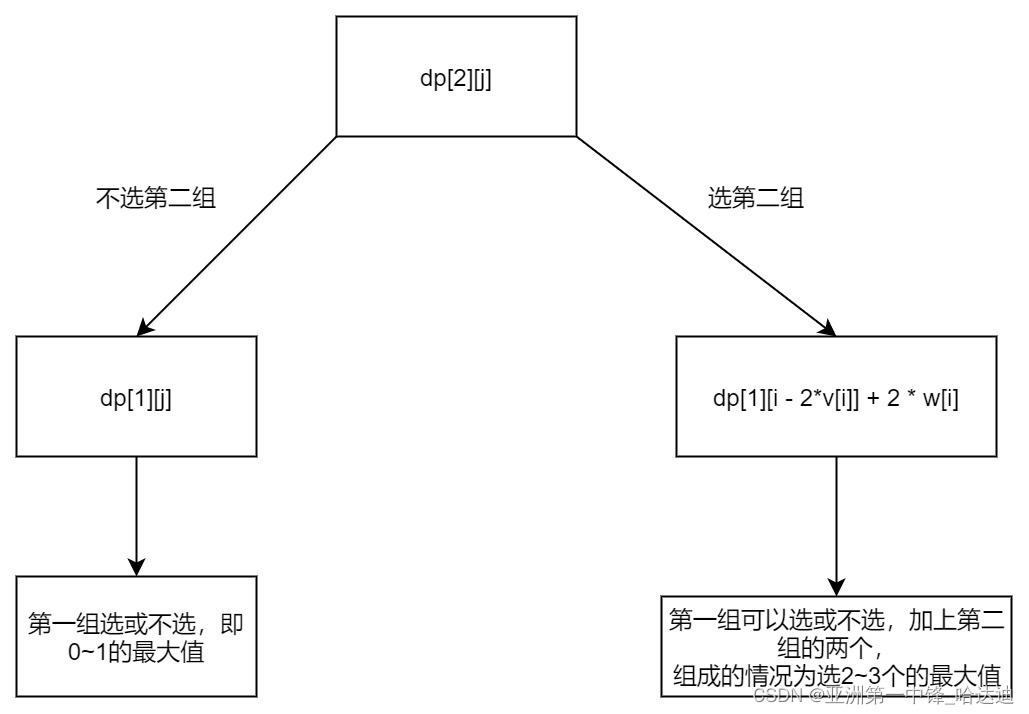
• dp[1][j] = max(dp[0][j], dp[0][j - v[i]] + w[i])

  • 表示第选0个和选1个的最大值

• dp[2][j] = max(dp[1][j], dp[1][j - 2*v[i]] + 2*w[i])

  • 表示选0到1个的最大值和选2到3的最大值即选0到3的最大值
  • 

• dp[3][j] = max(dp[2][j], dp[2][j - 4*v[i]] + 4*w[i])

  • 表示选0到3的最大值和选4到7的最大值即选0到7的最大值

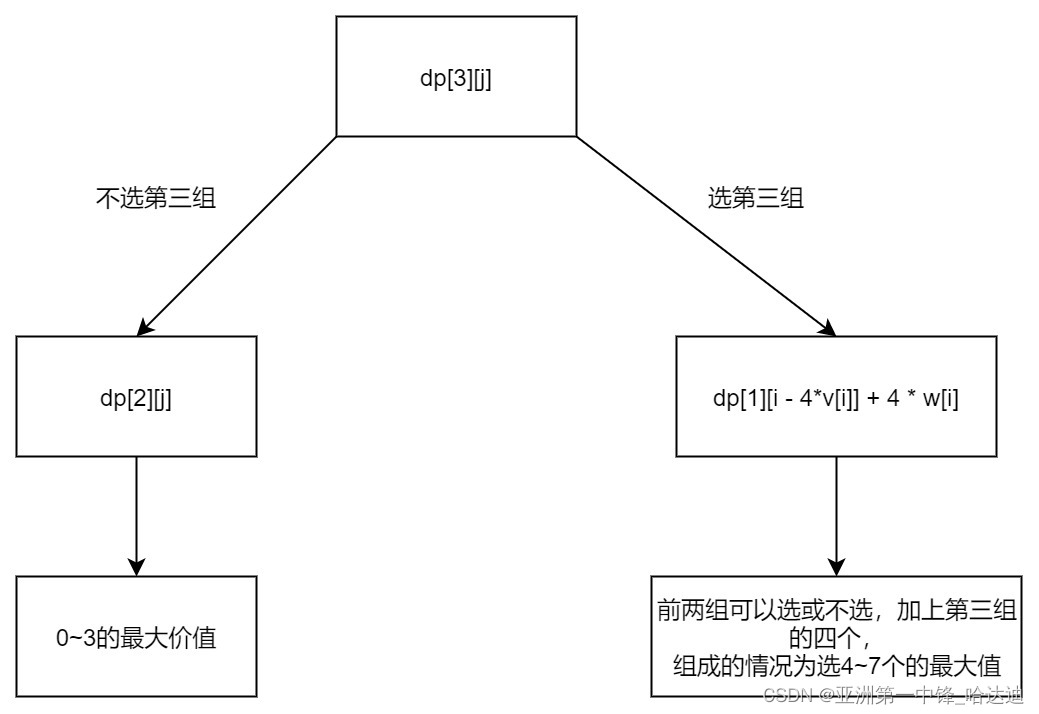
• 依次类推dp[5][j] = max(dp[4][j], dp[4][j - 4*v[i]] + 4*w[i])

  • 表示选0到15的最大值和选4到19的最大值即选0到19的最大值

因此将其按照二进制打包成更小的组在这些组上最01背包和原始问题是等价的

实现代码如下

public  static  int bagMulti(int N,int V,int[] w,int []v, int[] c) {
    // 开字够大的空间
    int[] neww = new  int[N * 32];
    int[] newv = new  int[N * 32];
    int cnt = 0;
    for (int i = 1;i<=N;i++) {
        int k = 1;
        while (k <= c[i]) {
            // 将每个物品按照二进制打包成不同的组构造成01背包问题
            cnt++;
            neww[cnt] = k * w[i];
            newv[cnt] = k * v[i];
            c[i] -= k;
            k *= 2;
        }

        if (c[i] >= 0) {
            cnt++;
            neww[cnt] = k * w[i];
            newv[cnt] = k * v[i];
        }
    }
    
    // 按照01背包模板计算
    int[] dp = new  int[cnt+1];
    for (int i = 1;i<=cnt;i++) {
        for (int j = V;j>=newv[i];j--) {
            dp[i] = Math.max(dp[i], dp[i - newv[i] + neww[i]);
        }
    }
    
    return dp[cnt];
}

假设c[i]的平均值为C这种做法的时间复杂度为O(NVlogC)