01背包

01背包0-1 Knapsack Problem
有$N$件物品和一个容量为$V$的背包。放入第$i$件物品耗费的费用是$C_i$,得到的价值为$W_i$。求解将哪些物品装入背包可以使价值总和最大

设$F\left[i,v\right]$表示前$i$件物品敲好放入一个容量为$v$的背包可以获得的最大价值容易写出
F [ i , v ] = max ⁡ { F [ i − 1 , v ] , F [ i − 1 , v − C i ] + W i } F\left[i,v\right] = \max\left\{F\left[i-1, v\right], F\left[i-1, v - C_i\right]+W_i\right\} F[i,v]=max{F[i−1,v],F[i−1,v−Ci​]+Wi​}
$F\left[0,0\right]=0$
时间复杂度$O\left(NV\right)$

初始化

初始化有两种一种是全$0$一种是$-\infty$
如果题目要求敲好装满就初始化$-\infty$
如果只是要求最大就初始化$0$

代码

当然这个代码容易MLE
洛谷P2871

#include<cstdio>
#include<algorithm>
const int N = 3405;
const int M = 12885;
int dp[N][M];

int main() {
	int n, m, w, d;
	scanf("%d%d", &n, &m);

	for (int i = 1; i <= n; ++i) {
		scanf("%d%d", &w, &d);
		for (int j = 1; j < w; ++j) {
			dp[i][j] = dp[i - 1][j];
		}
		for (int j = w; j <= m; ++j) {
			dp[i][j] = std::max(dp[i - 1][j], dp[i - 1][j - w] + d);
		}
	}
	printf("%d\n", dp[n][m]);


	return 0;
}

优化

虽然时间复杂度没法优化但是空间复杂度可以

容易发现我们只用到了上一行的状态因此我们最多需要两行数组
此时如果从后往前更新我们就只需要用一行数组

如果你从前往后更新相当于你放了好几次物品$i$,这样就不是01背包了

洛谷P2871

#include<cstdio>
#include<algorithm>
const int M = 12885;
int dp[M];

int main() {
	int n, m, w, d;
	scanf("%d%d", &n, &m);

	for (int i = 0; i < n; ++i) {
		scanf("%d%d", &w, &d);
		for (int j = m; j >= w; --j) {
			dp[j] = std::max(dp[j], dp[j - w] + d);
		}
	}
	printf("%d\n", dp[m]);


	return 0;
}

完全背包问题

01背包Complete Knapsack Problem

有$N$件物品和一个容量为$V$的背包。放入第$i$件物品耗费的费用是$C_i$,得到的价值为$W_i$每件物品可以无限使用求解将哪些物品装入背包可以使价值总和最大

如果沿用01背包的思路容易写出
f [ i , v ] = max ⁡ { f [ i − 1 , v − k C i ] + k W i ∣ 0 ≤ k C i ≤ v } f\left[i,v\right] = \max\left\{f\left[i-1, v - kC_i\right] + kW_i \mid 0\le kC_i \le v\right\} f[i,v]=max{f[i−1,v−kCi​]+kWi​∣0≤kCi​≤v}
但是这样大概的时间复杂度$O\left(NV\sum \frac{V}{C_i}\right)$

F [ i , v ] = max ⁡ { F [ i − 1 , v ] , F [ i , v − C i ] + W i } F\left[i,v\right] = \max\left\{F\left[i-1, v\right], F\left[i, v - C_i\right]+W_i\right\} F[i,v]=max{F[i−1,v],F[i,v−Ci​]+Wi​}
时间复杂度$O\left(NV\right)$

代码

洛谷P1616

#include<cstdio>
#include<algorithm>

const int M = 1e7 + 5;
long long dp[M];

int main() {
	int t, m, a, b;
	scanf("%d%d", &t, &m);

	for (int i = 0; i < m; ++i) {
		scanf("%d%d", &a, &b);
		for (int j = a; j <= t; ++j) {
			dp[j] = std::max(dp[j], dp[j - a] + b);
		}
	}
	printf("%lld\n", dp[t]);
	return 0;
}

多重背包

有$N$件物品和一个容量为$V$的背包。第$i$件物品最多有$M_i$件可用放入第$i$件物品耗费的费用是$C_i$,得到的价值为$W_i$。求解将哪些物品装入背包可以使价值总和最大

同样容易写出
$$f\left[i,v\right]=\max \left\{f\left[i-1,v-k{C}_i\right]+k{W}_i\mid 0\le k\le \min \left\{M_i,\lfloor \frac{v}{C_i}\rfloor \right\}\right\}$$
不过时间复杂度$O\left(V\sum M_i\right)$

二进制优化

如果$C_i{M}_i\ge V$则这个物品可以按照完全背包处理

一个数$m$可以分解为$1,2,4,\cdots ,2^{k-1},m-\left(2^k-1\right)$
其中$k$满足$m-\left(2^k-1\right)>0$
这些数可以组合成$\left[1,m\right]$中的任何数

也就是说我们可以把$m_i$拆分然后做01背包
时间复杂度$O\left(V\sum {\log }_2{M}_i\right)$

代码

洛谷P1776

#include<cstdio>
#include<algorithm>

const int M = 4e4 + 5;
int dp[M], W;

void complete_knapsack(int w, int v) {
	for (int j = w; j <= W; ++j) {
		dp[j] = std::max(dp[j], dp[j - w] + v);
	}
}

void zero_one_knapsack(int w, int v) {
	for (int j = W; j >= w; --j) {
		dp[j] = std::max(dp[j], dp[j - w] + v);
	}
}

int main() {
	int n, v, w, m;
	scanf("%d%d", &n, &W);
	for (int i = 0; i < n; ++i) {
		scanf("%d%d%d", &v, &w, &m);
		if (w * m >= W) {//完全背包
			complete_knapsack(w, v);
		}
		else { //二进制拆分, 转为01背包
			int k = 1, temp_w = w, temp_v = v;
			while (k < m) {
				zero_one_knapsack(temp_w, temp_v);
				m -= k;
				temp_w += temp_w;
				temp_v += temp_v;
				k += k;
			}
			//剩余
			w = m * w;
			v = m * v;
			zero_one_knapsack(w, v);
		}
	}
	printf("%d\n", dp[W]);
	return 0;
}

单调队列优化

$$f\left[i,v\right]=\max \left\{f\left[i-1,v-k{C}_i\right]+k{W}_i\mid 0\le k\le \min \left\{M_i,\lfloor \frac{v}{C_i}\rfloor \right\}\right\}$$

$v=k_1{C}_i+d,k_1=\lfloor \frac{v}{C_i}\rfloor ,d=v\mathrm{mod}{C}_i$
则
f [ i , k 1 C i + d ] = max ⁡ { f [ i − 1 , k 1 C i + d − k C i ] + k W i } = max ⁡ { f [ i − 1 , d + ( k 1 − k ) C i ] − ( k 1 − k ) W i } + k 1 W i \begin{aligned} f\left[i,k_1C_i +d\right] &= \max\left\{f\left[i-1, k_1C_i +d - kC_i\right] + kW_i \right\}\\ &= \max\left\{f\left[i-1, d + \left(k_1 - k\right)C_i \right] - \left(k_1-k\right)W_i \right\} + k_1 W_i\\ \end{aligned} f[i,k1​Ci​+d]​=max{f[i−1,k1​Ci​+d−kCi​]+kWi​}=max{f[i−1,d+(k1​−k)Ci​]−(k1​−k)Wi​}+k1​Wi​​
将$k_1-k$替换一下

f [ i , k 1 C i + d ] = max ⁡ { f [ i − 1 , d + k C i ] − k W i ∣ max ⁡ { 0 , k 1 − M i } ≤ k ≤ k 1 } + k 1 W i f\left[i,k_1C_i +d\right] = \max\left\{f\left[i-1, d+kC_i\right] -kW_i\mid \max\left\{0,k_1 - M_i\right\}\le k \le k_1\right\}+k_1W_i f[i,k1​Ci​+d]=max{f[i−1,d+kCi​]−kWi​∣max{0,k1​−Mi​}≤k≤k1​}+k1​Wi​
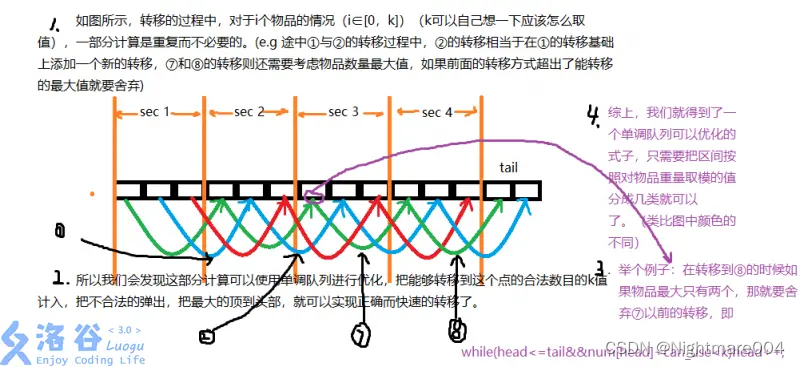
也就是说我们要维护一个窗口内的最大值可以考虑用单调队列
枚举$d$, 每次变化$k_1$和$k$变化$k_1$时维护窗口$\left[k_1-M_i,k_1\right]$的最大值

在固定$d$的情况下$k_1$至多有$\lfloor \frac{V-d}{C_i}\rfloor$种
而$d$有$C_i$种这样总的复杂度就是$O\left(V\right)$

#include<cstdio>
#include<algorithm>

const int M = 4e4 + 5;
int dp[M], W;
int q1[M], q2[M], head, tail;//单调递减队列q1存下标q2存值

int main() {
	int n, v, w, m, ans = 0;
	scanf("%d%d", &n, &W);
	for (int i = 0; i < n; ++i) {
		scanf("%d%d%d", &v, &w, &m);
		if (w == 0) {//防止除以0
			ans += m * v;
			continue;
		}
		for (int d = 0; d < w; ++d) {//枚举余数d
			head = 1;
			tail = 0;
			int max_k = (W - d) / w;
			int window_size = std::min(m, W / w);
			for (int k1 = 0; k1 <= max_k; ++k1) {
				int cur = dp[d + k1 * w] - k1 * v;
				while (head <= tail && cur >= q2[tail]) --tail;
				q1[++tail] = k1;
				q2[tail] = cur;
				//k1 - window_size <= k <= k1
				while (head <= tail && q1[head] < k1 - window_size)++head;
				dp[d + k1 * w] = std::max(dp[d + k1 * w], q2[head] + k1 * v);
			}
		}
	}
	printf("%d\n", ans + dp[W]);
	return 0;
}

混合背包

就是01背包完全背包多重背包结合

做法就是判断每个物品属于哪种背包
洛谷P1833
我这里多重背包用的单调队列优化的
似乎二进制优化也可以过

#include<cstdio>
#include<algorithm>

const int M = 1005;
int dp[M], W;
int q1[M], q2[M], head, tail;

void complete_knapsack(int w, int v) {
	for (int j = w; j <= W; ++j) {
		dp[j] = std::max(dp[j], dp[j - w] + v);
	}
}

void zero_one_knapsack(int w, int v) {
	for (int j = W; j >= w; --j) {
		dp[j] = std::max(dp[j], dp[j - w] + v);
	}
}

void multi_knapsack(int w, int v, int m) {
	//需要保证w不为0
	for (int d = 0; d < w; ++d) {//枚举余数d
		head = 1;
		tail = 0;
		int max_k = (W - d) / w;
		int window_size = std::min(m, W / w);
		for (int k1 = 0; k1 <= max_k; ++k1) {
			int cur = dp[d + k1 * w] - k1 * v;
			while (head <= tail && cur >= q2[tail]) --tail;
			q1[++tail] = k1;
			q2[tail] = cur;
			//k1 - window_size <= k <= k1
			while (head <= tail && q1[head] < k1 - window_size)++head;
			dp[d + k1 * w] = std::max(dp[d + k1 * w], q2[head] + k1 * v);
		}
	}
}

int main() {
	int nx, ny, ex, ey, n;
	scanf("%d:%d%d:%d%d", &nx, &ny, &ex, &ey, &n);
	W = (ex * 60 + ey) - (nx * 60 + ny);
	int t, c, p, ans = 0;
	for (int i = 0; i < n; ++i) {
		scanf("%d%d%d", &t, &c, &p);
		if (t == 0) {
			//应该没有这种情况
			//if (p == 0) ans = 0x7fffffff;
			ans += c * p;
		}
		else if (p == 0 || t * p >= W) {//完全背包
			complete_knapsack(t, c);
		}
		else if (p == 1) {//01背包
			zero_one_knapsack(t, c);
		}
		else {
			multi_knapsack(t, c, p);
		}
	}
	printf("%d\n", ans + dp[W]);
	return 0;
}

二维费用的背包问题

设第$i$件物品所需的两种费用为$C_i$和$D_i$两种费用可付出的最大值背包容量分别为$V,U$物品价值为$W_i$问怎样选择物品可以得到最大的价值

设$F\left[i,v,u\right]$表示前$i$件物品付出两种费用分别为$v$和$u$时可获得的最大价值于是
F [ i , u , v ] = max ⁡ { F [ i − 1 , v , u ] , F [ i − 1 , v − C i , u − D i ] + W i } F\left[i,u,v\right] = \max \left\{F\left[i-1,v,u\right], F\left[i-1,v-C_i,u-D_i\right] + W_i\right\} F[i,u,v]=max{F[i−1,v,u],F[i−1,v−Ci​,u−Di​]+Wi​}

代码

洛谷P1855
这里价值为1

#include<cstdio>
#include<algorithm>

const int V = 205;
const int U = 205;

int dp[V][U];

int main() {
	int n, M, T, m, t;
	scanf("%d%d%d", &n, &M, &T);
	for (int i = 0; i < n; ++i) {
		scanf("%d%d", &m, &t); // 价值为1
		for (int j = M; j >= m; --j) {
			for (int k = T; k >= t; --k) {
				dp[j][k] = std::max(dp[j][k], dp[j - m][k - t] + 1);
			}
		}
	}
	printf("%d\n", dp[M][T]);
	return 0;
}

分组的背包问题

有$N$件物品和一个容量为$V$的背包。第$i$件物品的费用时$C_i$价值是$W_i$。这些物品被划分为$K$组每组中的物品互相冲突最多选一件。求解将哪些物品装入背包可使这些物品的费用综合不超过背包容量且价值最大

这个问题其实就相当于每一组中选一件还是一件都不选
设$F\left[k,v\right]$表示前$k$组物品花费费用$v$能取得的最大权值则
F [ k , v ] = max ⁡ { F [ k − 1 , v ] , F [ k − 1 , v − C i ] + W i ∣ i t e m   i ∈ g r o u p   k } F\left[k,v\right] = \max\left\{F\left[k-1,v\right], F\left[k-1,v-C_i\right] + W_i \mid item\ i \in group\ k\right\} F[k,v]=max{F[k−1,v],F[k−1,v−Ci​]+Wi​∣item i∈group k}
循环的时候先循环$V$再循环组内物品

代码

洛谷P1757

#include<cstdio>
#include<algorithm>

const int N = 1005;
const int M = 1005;

int w[N];
int v[N];
int g[N][N];//g[i][j]表示第i组第j个物品是g[i][j]
int cnt[N];//cnt[i]表示第i组有几个物品
int dp[M];

int main() {
	int m, n, c, max_group = 0;
	scanf("%d%d", &m, &n);

	for (int i = 0; i < n; ++i) {
		scanf("%d%d%d", &w[i], &v[i], &c);
		g[c][cnt[c]] = i;
		++cnt[c];
		max_group = std::max(max_group, c);
	}
	for (int i = 0; i <= max_group; ++i) {
		if (cnt[i] == 0)continue;
		for (int j = m; j >= 0; --j) {
			for (int k = 0; k < cnt[i]; ++k) {
				int idx = g[i][k];
				if (w[idx] <= j) {
					dp[j] = std::max(dp[j], dp[j - w[idx]] + v[idx]);
				}
			}
		}
	}
	printf("%d\n", dp[m]);
	return 0;
}

有依赖的背包问题

物品$i$依赖于物品$j$即选了物品$i$就必须选物品$j$但是选了物品$j$不一定要选物品$i$

简化版

只有一层依赖并且没有循环依赖

一般版

没有循环依赖但是有多层依赖

树形dp从叶子一层一层向上
相当于先跑孩子的然后孩子里跑一遍01背包最后加上当前节点

代码

acwing10

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;

const int MAXN = 105;
const int MAXV = 105;

vector<int> edge[MAXN];
int dp[MAXN][MAXV], V;
int v[MAXN];
int w[MAXN];

void dfs(int u) {
	for (int i = 0; i < edge[u].size(); ++i) {
		int son = edge[u][i];
		dfs(son);
		for (int j = V - v[u]; j >= 0; --j) {//遍历除去当前节点体积后的所有体积
			for (int k = j; k >= 0; --k) {//遍历决策
				dp[u][j] = std::max(dp[u][j], dp[u][j - k] + dp[son][k]);
			}
		}
	}
	for (int i = V; i >= v[u]; --i) {//加上当前节点
		dp[u][i] = dp[u][i - v[u]] + w[u];
	}
	for (int i = v[u] - 1; i >= 0; --i) {//装不下当前节点方案不可行
		dp[u][i] = 0;
	}
}

int main() {
	int p, root, N;
	scanf("%d%d", &N, &V);
	for (int i = 1; i <= N; ++i) {
		scanf("%d%d%d", &v[i], &w[i], &p);
		if (p != -1)edge[p].push_back(i);
		else root = i;

	}
	dfs(root);
	printf("%d\n", dp[root][V]);
	return 0;
}

洛谷P1064
这里因为都是10的倍数所以可以同时除以10不然会T

#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;

const int N = 65;
const int M = 3.2e3 + 5;

vector<int> edge[N];

int dp[N][M], m;
int w[N];
int v[N];

void dfs(int u) {
	for (int i = 0; i < edge[u].size(); ++i) {
		int son = edge[u][i];
		dfs(son);
		for (int j = m - w[u]; j >= 0; --j) {
			for (int k = j; k >= 0; --k) {
				dp[u][j] = max(dp[u][j], dp[u][j - k] + dp[son][k]);
			}
		}
	}
	for (int i = m; i >= w[u]; --i) {
		dp[u][i] = dp[u][i - w[u]] + v[u];
	}
	for (int i = w[u] - 1; i >= 0; --i) {
		dp[u][i] = 0;
	}
}

int main() {
	int n, q;
	scanf("%d%d", &m, &n);
	m /= 10;
	for (int i = 1; i <= n; ++i) {
		scanf("%d%d%d", &w[i], &v[i], &q);
		w[i] /= 10;
		v[i] *= w[i];
		edge[q].push_back(i);
	}
	dfs(0);
	printf("%d\n", dp[0][m] * 10);
	return 0;
}

泛化物品

再背包容量为$V$的背包问题中泛化物品时一个定义域为$0,\cdots ,V$中的整数的函数$h$当分配给他的费用为$v$时能得到的价值就是$h\left(v\right)$

例如01背包就是$h\left(v\right)=\{\begin{array}{ll}w,& v=c\\ 0,& otherwise\end{array}$

再说…

其他

输出具体方案

以01背包为例

用二维的数组
如果不要求字典序可以考虑从右下角开始
如果$dp[i][j]=dp[i-1][j]$那么说明没有用物品$i$就向上走
否则使用了物品$i$则跳到$dp[i-1][j-w[i]]$

最后一直跳到$dp[0][0]$

另一种是使用二维bool数组
dp的时候如果不使用物品$i$$g[i][j]=false$,否则$g[i][j]=true$
剩下的就是跟上面一样

字典序
逆序存物品输出的时候再变换回来

代码

acwing12

#include<cstdio>

const int MAXN = 1005;
const int MAXM = 1005;

int dp[MAXM], V;
bool g[MAXN][MAXM];
int v[MAXN];
int w[MAXN];

int main() {
	int N;
	scanf("%d%d", &N, &V);
	for (int i = N; i >= 1; --i) {
		scanf("%d%d", &v[i], &w[i]);
	}
	for (int i = 1; i <= N; ++i) {
		for (int j = V; j >= v[i]; --j) {
			int temp = dp[j - v[i]] + w[i];
			if (temp >= dp[j]) {
				dp[j] = temp;
				g[i][j] = true;
			}
		}
	}

	bool flag = false;
	int x = N, y = V;
	while (x > 0) {
		if (g[x][y]) {
			y -= v[x];
			if (flag) {
				printf(" ");
			}
			else {
				flag = true;
			}
			printf("%d", N - x + 1);
		}
		--x;
	}
	printf("\n");
	return 0;
}

求方案总数

把之前的$\max$,换成$sum$

求最优方案总数

设$f[i][j]$为只能放前$i$个物品的情况下容量为$j$的背包正好装满所能到达的最大价值
$g[i][j]$为只能放前$i$个物品的情况下容量为$j$的背包正好装满的方案数

代码

acwing11

#include<cstdio>
#include<cstring>
#include<algorithm>

const int M = 1005;
const int mod = 1e9 + 7;

int dp[M], V;
int g[M] = { 1 };

int main() {
	memset(dp, 0xc0, sizeof(dp));
	dp[0] = 0;
	int N, v, w;
	scanf("%d%d", &N, &V);
	for (int i = 0; i < N; ++i) {
		scanf("%d%d", &v, &w);
		for (int j = V; j >= v; --j) {
			int temp = std::max(dp[j], dp[j - v] + w);
			int cnt = 0;
			if (dp[j] == temp) cnt = (cnt + g[j]) % mod;
			if (dp[j - v] + w == temp)cnt = (cnt + g[j - v]) % mod;
			dp[j] = temp;
			g[j] = cnt;
		}
	}
	int ans = 0;
	for (int i = 0; i <= V; ++i) {
		ans = std::max(ans, dp[i]);
	}
	int res = 0;
	for (int i = 0; i <= V; ++i) {
		if (dp[i] == ans)res = (res + g[i]) % mod;
	}
	printf("%d\n", res);
	return 0;
}

第 k 优解

再说

参考
https://github.com/tianyicui/pack