机器学习实战教程(九):模型泛化
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
泛化能力
模型泛化是指机器学习模型对新的、未见过的数据的适应能力。在机器学习中我们通常会将已有的数据集划分为训练集和测试集使用训练集训练模型然后使用测试集来评估模型的性能。模型在训练集上表现得好并不一定能在测试集或实际应用中表现得好。因此我们需要保证模型具有良好的泛化能力才能确保其在实际场景中的效果。
为了提高模型的泛化能力我们通常需要采取一系列措施例如增加数据集的大小、特征选择、特征缩放、正则化、交叉验证等。通过这些方法可以减少模型的过拟合提高对新数据的预测能力。
总之模型泛化是机器学习中非常重要的一个概念。它直接关系到模型在实际应用中的效果并且也是评估机器学习算法和模型的重要指标之一。
模型评价与选择
差错分析
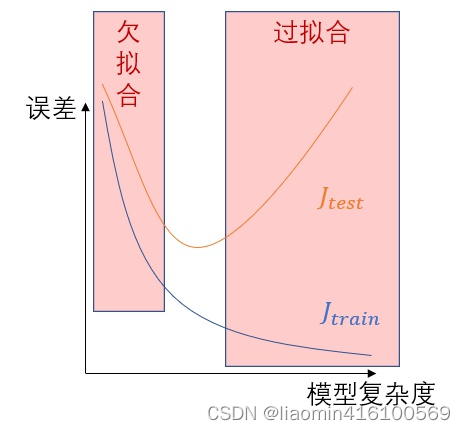
机器预测时就好像在投飞镖越接近靶心则预测越准。可以把差错分为两类偏差bias和方差variance。可以用下图来形象描绘

具体到学习任务上若假设函数取得不够好拟合结果可能会出现两种问题
- 欠拟合underfit参数过少假设函数太不自由过于简单连样本集都拟合不好预测时容易偏向一侧偏差大。
- 过拟合overfit参数过多假设函数太自由不抗干扰对样本集拟合得很好但是假设函数过于畸形预测时忽左忽右方差大。
欠拟合与过拟合可用下图来形象地说明

在改变模型的复杂度和训练集大小时训练集和测试集的误差的函数图改变模型复杂度时的误差
改变数据集时的误差
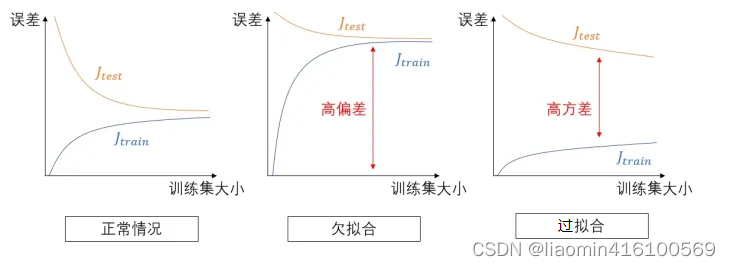
解决欠拟合比较简单增加参数或增加特征就行了麻烦的是过拟合。
解决过拟合的办法有
- 减少该模型的参数或者改为更简单的模型。
- 正则化。
- 增大训练集减少噪音成分等。
泛化误差
θ \theta θ代表超参数 J 未知 J_{未知} J未知 { \{ { θ \theta θ } \} }代表训练出模型 θ \theta θ参数后对于未知数据的误差越小泛化能力越强 J t e s t J_{test} Jtest { \{ { θ \theta θ } \} }代表模型对测试机的误差越小泛化能力越强。
我们希望我们的模型有泛化能力即面对未训练到的、未知的情景也能发挥作用。泛化误差generalization error指的是模型在处理未知数据时的代价函数
J
未知
J_{未知}
J未知
{
\{
{
θ
\theta
θ
}
\}
}
的值它可以量化模型的泛化能力。
然而我们训练和测试模型时并没有未知的数据。我们会根据模型在训练集上的表现改进模型再进行训练与测试。但在测试集上最终算出的
J
t
e
s
t
J_{test}
Jtest
{
\{
{
θ
\theta
θ
}
\}
}已经对测试集进行优化了它明显对泛化误差的估计过于乐观会偏低。也就是说把模型放在实际应用中的效果会比预想的差很多。
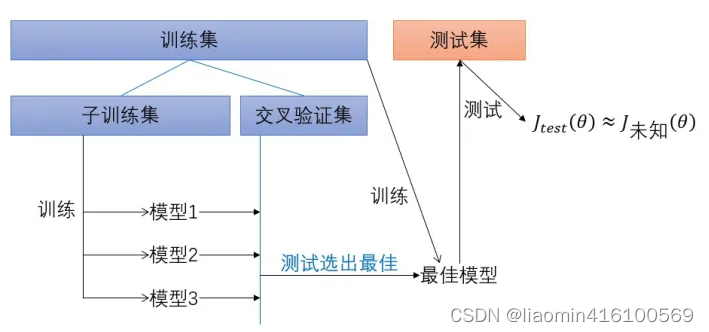
为了解决这个问题人们提出了交叉验证cross validation的方法
交叉验证
交叉验证的步骤
- 把训练集进一步分为子训练集与交叉验证集。把测试集藏好先不用它。测试集是对未知数据的模拟
- 使用各种不同的模型在子训练集上训练并测出各模型在交叉验证集上的 J c v J_{cv} Jcv { \{ { θ \theta θ } \} }
- 选择 J c v J_{cv} Jcv { \{ { θ \theta θ } \} }最小的模型认为它最佳。把子训练集和交叉验证集合并为训练集训练出最终的模型。
交叉验证的改进方法是K折K-fold交叉验证图6把训练集分为许多小块每一种情况取其中一小块作为交叉验证集其余部分合并作为子训练集求出该模型的
J
c
v
J_{cv}
Jcv
{
\{
{
θ
\theta
θ
}
\}
}把每一种情况算遍求出该模型的平均
J
c
v
J_{cv}
Jcv
{
\{
{
θ
\theta
θ
}
\}
}认为平均最小的模型为最佳模型。最终仍然是用整个训练集训练最佳模型在测试集上估计泛化误差。
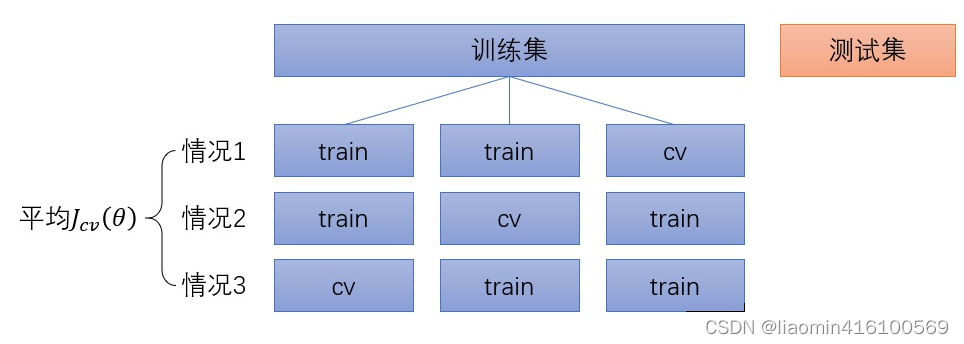
K折交叉验证的优点是进一步确保交叉验证集没有特殊性对泛化误差的估计更为准确。
KFold拆分
在sklearn中我们可以使用KFold类来实现k折交叉验证。
在进行k折交叉验证时KFold对象会将原始数据集随机分成k个近似大小的子集每个子集称为“折”fold。比如10个元素数组k=5的话会拆分为5个数据集每个折数据集就是2个5个折数据集都会被作为一次测试机所以会有5个组合。
from sklearn.model_selection import KFold
import numpy as np
# 创建一个包含10个元素的数组作为样本数据
X = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# 定义K值
k = 5
# 创建KFold对象并指定n_splits参数为K
kf = KFold(n_splits=k)
# 遍历KFold对象中的每一组训练集和测试集
for train_index, test_index in kf.split(X):
print("train_index:", train_index, "test_index:", test_index)
输出结果如下
train_index: [2 3 4 5 6 7 8 9] test_index: [0 1]
train_index: [0 1 4 5 6 7 8 9] test_index: [2 3]
train_index: [0 1 2 3 6 7 8 9] test_index: [4 5]
train_index: [0 1 2 3 4 5 8 9] test_index: [6 7]
train_index: [0 1 2 3 4 5 6 7] test_index: [8 9]
fold的值也就决定了最后使用cv数据集验证的得分个数。
cross_val_score实战
cross_val_score函数是Scikit-learn库中用于评估模型性能的快速方法之一。它计算基于交叉验证的模型评分并返回每个fold的测试性能得分。与KFold不同cross_val_score不需要显示拆分数据集。您只需提供模型和数据集即可进行评估该函数将自动处理交叉验证过程从而使代码更加简洁和易于理解。
数据集和模型
load_digits 是 Scikit-learn 库中的一个函数用于加载手写数字图像数据集。这个数据集包含 8x8 像素大小的 1797 张手写数字图像每张图像都对应一个 0 到 9 的数字标签。
from sklearn.datasets import load_digits
digits = load_digits()
import matplotlib.pyplot as plt
fig, axes = plt.subplots(nrows=1, ncols=5, figsize=(10, 3))
for i, ax in enumerate(axes):
ax.imshow(digits.images[i], cmap='gray')
ax.set_title(digits.target[i])
plt.show()

在Scikit-learn库中的KNeighborsClassifier实现了k近邻算法其中的超参数k和p影响着模型的性能。
- n_neighbors即k指定要考虑的最近邻居的个数。默认情况下它为5表示预测一个新样本时将使用数据集中距离其最近的5个数据点的标签,5个中最多的那个标签就是当前数据的标签。
- p用于计算距离的指标。默认情况下使用Minkowski距离p 为2表示使用欧几里得距离。不同的 p 值对应不同的距离度量方式例如p=1 表示曼哈顿距离p=3 可以使用一种更为复杂的曼哈顿距离度量方式。
使用数据集和测试集获取最佳kp
将数据集拆分为训练集和测试集然后k从1到11p从1到6测试训练集的得分得到最佳的k和p。
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
digits = datasets.load_digits()
x = digits.data
y = digits.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.4, random_state=666)
best_score, best_p, best_k = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
knn_clf.fit(x_train, y_train)
score = knn_clf.score(x_test, y_test)
if score > best_score:
best_score, best_p, best_k = score, p, k
print("Best K=", best_k)
print("Best P=", best_p)
print("Best score=", best_score)
输出结果
Best K= 3
Best P= 4
Best score= 0.9860917941585535
使用交叉验证获取最佳kp
cross_val_score函数默认使用的交叉验证方法是3-Fold交叉验证即将数据集分为3个相等的部分其中2个部分用于训练1个部分用于测试。在每个fold迭代中使用测试集得到性能度量得分然后将所有fold的结果平均并返回。
需要注意的是cross_val_score还有一个名为cv的参数可以用来指定交叉验证的折叠数量即k值。例如cv=5表示5-Fold交叉验证将数据集拆分为5个相等的部分其中4个部分用于训练1个部分用于测试。对于分类问题和回归问题通常选择 3, 5 或 10 折交叉验证。通常交叉验证的折叠数量越多模型的评估结果越可靠但计算成本也会增加。
总之在没有显式设置cv参数时默认情况下cross_val_score使用的是3-Fold交叉验证即默认的k值是3。
best_score, best_p, best_k = 0, 0, 0
for k in range(2, 11):
for p in range(1, 6):
knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
scores = cross_val_score(knn_clf, x_train, y_train)
score = np.mean(scores)
if score > best_score:
best_score, best_p, best_k = score, p, k
print("Best K=", best_k)
print("Best P=", best_p)
print("Best score=", best_score)
输出
Best K= 2
Best P= 2
Best score= 0.9823599874006478
对比第一种情况我们发现得到的最优超参数是不一样的虽然score会稍微低一些但是一般第二种情况更加可信。但是这个score只是说明这组参数最优并不是指的是模型对于测试集的准确率因此接下来看一下准确率。
best_knn_clf = KNeighborsClassifier(weights='distance', n_neighbors=2, p=2)
best_knn_clf.fit(x_train, y_train)
best_knn_clf.score(x_test, y_test)
输出结果0.980528511821975这才是模型的准确度。
正则化regularization
原理
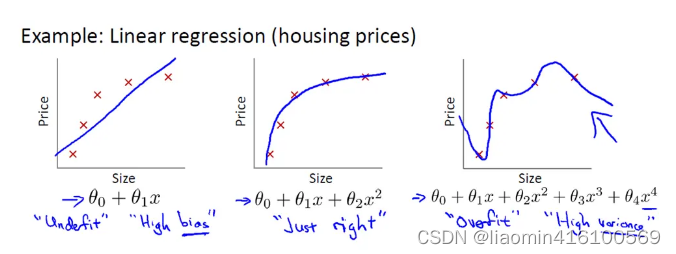
想要理解什么是正则化首先我们先来了解上图的方程式。当训练的特征和数据很少时往往会造成欠拟合的情况对应的是左边的坐标而我们想要达到的目的往往是中间的坐标适当的特征和数据用来训练但往往现实生活中影响结果的因素是很多的也就是说会有很多个特征值所以训练模型的时候往往会造成过拟合的情况如上图所示。
以图中的公式为例往往我们得到的模型是
θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 + θ 4 x 4 \theta_{0}+\theta_{1}x+\theta_{2}x^2+\theta_{3}x^3+\theta_{4}x^4 θ0+θ1x+θ2x2+θ3x3+θ4x4
为了能够得到中间坐标的图形肯定是希望θ3和θ4越小越好因为这两项越小就越接近于0就可以得到中间的图形了。
对于损失函数:
(
1
2
m
[
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
2
]
)
({1\over2m}[\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)^2}])
(2m1[i=1∑m(hθ(xi)−yi)2])
在线性回归中就是通过最小二乘法计算损失函数的最小值
m
i
n
(
1
2
m
[
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
2
]
)
min({1\over2m}[\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)^2}])
min(2m1[i=1∑m(hθ(xi)−yi)2])
而计算出每个特征的
θ
\theta
θ值。
如果损失函数加上一个数求最小值那个这个数肯定越趋近于0最小是肯定越小
那么这个值加什么了我们是希望
θ
\theta
θ趋近于0对于损失函数的影响越小越好也就是减少特征。
把公式通用化得
1
2
m
[
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
2
]
)
+
λ
∑
j
=
1
n
θ
j
2
{1\over2m}[\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)^2}])+\lambda\sum_{j=1}^{n}\theta_{j}^2
2m1[i=1∑m(hθ(xi)−yi)2])+λj=1∑nθj2
为了损失函数求得最小值使θ值趋近于0这就达到了我们的目的。
相当于在原始损失函数中加上了一个惩罚项(λ项)
这就是防止过拟合的一个方法通常叫做L2正则化也叫作岭回归。
我们可以认为加入L2正则项后估计参数长度变短了这在数学上被称为特征缩减shrinkage。
shrinkage方法介绍指训练求解参数过程中考虑到系数的大小通过设置惩罚系数使得影响较小的特征的系数衰减到0只保留重要特征的从而减少模型复杂度进而达到规避过拟合的目的。常用的shinkage的方法有LassoL1正则化和岭回归L2正则化等。
LassoL1正则化公式
1
2
m
[
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
2
]
+
λ
∑
j
=
1
n
∣
θ
j
∣
{1\over2m}[\sum_{i=1}^{m}{(h_\theta(x^i)-y^i)^2}]+\lambda\sum_{j=1}^{n}|\theta_{j}|
2m1[i=1∑m(hθ(xi)−yi)2]+λj=1∑n∣θj∣
上面的逻辑可能看出是拉格朗日乘子法的应用
采用shrinkage方法的主要目的包括两个
- 一方面因为模型可能考虑到很多没必要的特征这些特征对于模型来说就是噪声shrinkage可以通过消除噪声从而减少模型复杂度
- 另一方面模型特征存在多重共线性变量之间相互关联的话可能导致模型多解而多解模型的一个解往往不能反映模型的真实情况shrinkage可以消除关联的特征提高模型稳定性。
对应图形
我们可以简化L2正则化的方程
J
=
J
0
+
λ
∑
w
w
2
J=J_{0}+\lambda\sum_ww^2
J=J0+λ∑ww2
J0表示原始的损失函数咱们假设正则化项为
假设是2个特征w有两个值w1和w2
L
=
λ
(
w
1
2
+
w
2
2
)
L=\lambda(w_{1}^2+w_{2}^2)
L=λ(w12+w22)
我们不妨回忆一下圆形的方程
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
(x-a)^2+(y-b)^2=r^2
(x−a)2+(y−b)2=r2
其中(a,b)为圆心坐标r为半径。那么经过坐标原点的单位元可以写成
正和L2正则化项一样同时机器学习的任务就是要通过一些方法比如梯度下降求出损失函数的最小值。
此时我们的任务变成在L约束下求出J0取最小值的解(拉格朗日乘子法)。
求解J0的过程可以画出等值线。同时L2正则化的函数L也可以在w1w2的二维平面上画出来。如下图
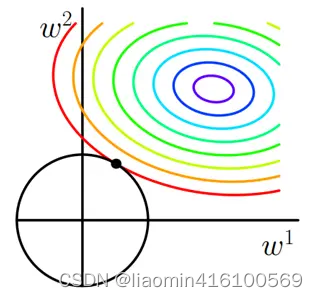
L表示为图中的黑色圆形随着梯度下降法的不断逼近与圆第一次产生交点而这个交点很难出现在坐标轴上。
这就说明了L2正则化不容易得到稀疏矩阵同时为了求出损失函数的最小值使得w1和w2无限接近于0达到防止过拟合的问题。
岭回归Ridege Regression
就是L2正则化
测试用例
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
plt.scatter(x, y)
plt.show()

使用20项式来进行拟合模拟过拟合
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
def PolynomiaRegression(degree):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scale', StandardScaler()),
('lin_reg', LinearRegression()),
])
np.random.seed(666)
x_train, x_test, y_train, y_test = train_test_split(X, y)
poly_reg = PolynomiaRegression(degree=20)
poly_reg.fit(x_train, y_train)
y_poly_predict = poly_reg.predict(x_test)
print(mean_squared_error(y_test, y_poly_predict))
# 167.9401085999025
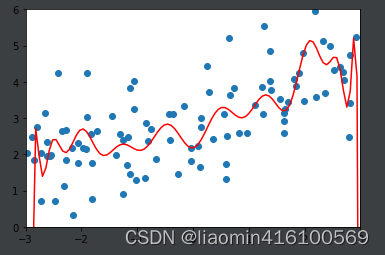
import matplotlib.pyplot as plt
x_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly_reg.predict(x_plot)
plt.scatter(x, y)
plt.plot(x_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
封装一个函数生成测试集并测试模型
def plot_model(model):
x_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = model.predict(x_plot)
plt.scatter(x, y)
plt.plot(x_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
使用岭回归
from sklearn.linear_model import Ridge
def RidgeRegression(degree, alpha):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scale', StandardScaler()),
('lin_reg', Ridge(alpha=alpha)),
])
ridege1_reg = RidgeRegression(20, alpha=0.0001)
ridege1_reg.fit(x_train, y_train)
y1_predict = ridege1_reg.predict(x_test)
print(mean_squared_error(y_test, y1_predict))
# 跟之前的136.相比小了很多
plot_model(ridege1_reg)
输出误差1.3233492754136291

调整
α
\alpha
α=1
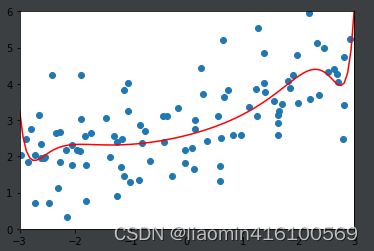
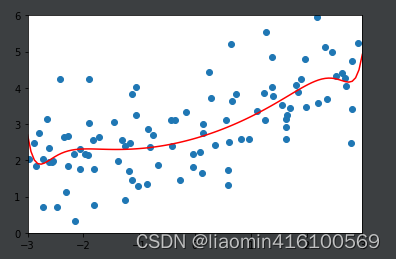
ridege2_reg = RidgeRegression(20, alpha=1)
ridege2_reg.fit(x_train, y_train)
y2_predict = ridege2_reg.predict(x_test)
print(mean_squared_error(y_test, y2_predict))
plot_model(ridege2_reg)
输出1.1888759304218461
调整
α
\alpha
α=100
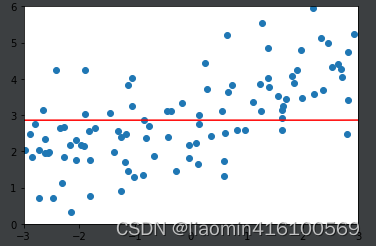
ridege2_reg = RidgeRegression(20, alpha=100)
ridege2_reg.fit(x_train, y_train)
y2_predict = ridege2_reg.predict(x_test)
print(mean_squared_error(y_test, y2_predict))
# 1.3196456113086197
plot_model(ridege2_reg)
输出1.3196456113086197
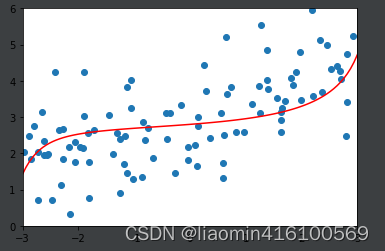
调整
α
\alpha
α=1000000
ridege2_reg = RidgeRegression(20, alpha=1000000)
ridege2_reg.fit(x_train, y_train)
y2_predict = ridege2_reg.predict(x_test)
print(mean_squared_error(y_test, y2_predict))
# 1.8404103153255003
plot_model(ridege2_reg)
输出1.8404103153255003
通过上面几种alpha的取值可以看出我们可以在1-100进行更加细致的搜索找到最合适的一条相对比较平滑的曲线去拟合。这就是L2正则。
LASSO Regularization
封装
#%%
import numpy as np
import matplotlib.pyplot as plt
from skimage.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
np.random.seed(666)
x_train, x_test, y_train, y_test = train_test_split(X, y)
plt.scatter(x, y)
plt.show()
#%%
from sklearn.linear_model import Lasso
def plot_model(model):
x_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = model.predict(x_plot)
plt.scatter(x, y)
plt.plot(x_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
def LassoRegression(degree, alpha):
return Pipeline([
('poly', PolynomialFeatures(degree=degree)),
('std_scale', StandardScaler()),
('lin_reg', Lasso(alpha=alpha)),
])
def TestRegression(degree, alpha):
lasso1_reg = LassoRegression(degree, alpha)
#这里相比Ridge的alpha小了很多这是因为在Ridge中是平方项
lasso1_reg.fit(x_train, y_train)
y1_predict = lasso1_reg.predict(x_test)
print(mean_squared_error(y_test, y1_predict))
# 1.149608084325997
plot_model(lasso1_reg)
使用lasso回归
调整
α
\alpha
α=0.01
TestRegression(20,0.01)
输出1.149608084325997
调整 α \alpha α=0.1
TestRegression(20,0.1)
输出1.1213911351818648

调整
α
\alpha
α=1
TestRegression(20,1)
输出1.8408939659515595

解释Ridge和LASSO

通过这两幅图进行对比发现LASSO拟合的模型更倾向于是一条直线而Ridge拟合的模型更趋向与一条曲线。这是因为两个正则的本质不同Ridge是趋向于使所有
的加和尽可能的小而Lasso则是趋向于使得一部分
的值变为0因此可作为特征选择用这也是为什么叫Selection Operation的原因。
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

