期权定价数值方法之蒙特卡洛模拟【python量化】

阿里云国内75折 回扣 微信号：monov8
阿里云国际，腾讯云国际，低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号：monov8 飞机：@monov6

期权定价数值方法之蒙特卡洛模拟

前言

蒙特卡洛模拟最重要的应用之一是对未定权益如期权、衍生品、混合型工具的估值。在风险世界中未定权益的价值是风险中立鞅测度下的折现后的预期收益。

一、蒙特卡洛模拟思路

蒙特卡洛模拟需要用到风险中立世界思想。其基本思路为尽可能的模拟风险中性世界中标的资产价格的多种路径计算每种路径下的期权回报均值再贴现就可得期权价格。
①在风险中性世界里对S的随机路径进行抽样这就给出了标的资产价格路径的一个实现。
②计算这条路径下的期权回报。
③重复计算步骤①、②得到许多样本结果即风险中性世界中的期权回报值。
④计算这些回报的均值得到风险中性世界中的预期期权回报值。
⑤用无风险利率进行贴现得到这个期权的估计价值。
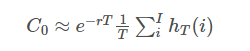
在这里插入图片描述

二、随机过程

前文说到蒙特卡洛模拟方法需要模拟标的资产的价格路径而价格路径的变化是随机的可以通过数学上的随机过程进行模型。因此本部分将介绍集中主流的随机过程。

粗略地讲随机过程是一个随机变量序列。但是随机数的选取一般不是独立的而是依赖于前几次选取的结果。不过金融学中使用的随机过程通常表现出马尔科夫特性 ——主要的含义是明天的过程值只依赖于今天的过程状态而不依赖其他任何“历史”状态甚至不依赖整个路径历史。这种过程也被称做“无记忆过程 ”

1.几何布朗运动

根据Black-Scholes模型在风险中性世界中标的资产价格变量遵循几何布朗运动几何布朗运动的数学公式为
在这里插入图片描述
式中的Zt 是标准布朗运动SDE被称作几何布朗运动。St 的值呈对数正态分布。

几何布朗运动的代码实现如下所示

# 随机过程
# 几何布朗运动
S0=100
r=0.05
sigma=0.25
T=2
I=10000
M=50
dt=T/M
S=np.zeros((M+1,I))
S[0]=S0
for t in range(1,M+1):
    S[t]=S[t-1]*np.exp((r-0.5*sigma**2)*dt+sigma*np.sqrt(dt)*npr.standard_normal(I))
plt.figure(figsize=(10,8))
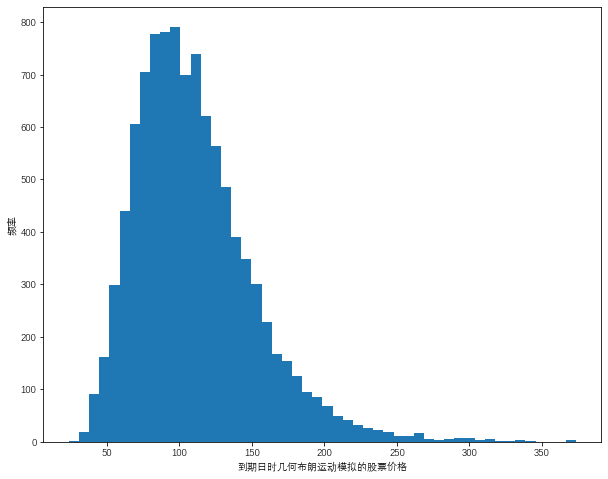
plt.hist(S[-1],bins=50)
plt.xlabel('到期日时几何布朗运动模拟的股票价格')
plt.ylabel('频率')

plt.figure(figsize=(10,8))
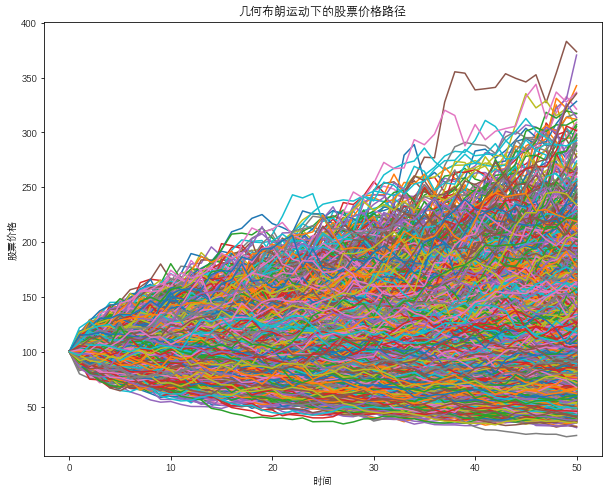
plt.plot(S[:100],lw=1.5)
plt.xlabel('时间')
plt.ylabel('股票价格')
plt.title('几何布朗运动下的股票价格路径')

这里假设标的资产的初始价格为100利率r为0.05波动率为0.25。从图中可以看出几何布朗运动模拟标的资产价格路径呈现对数正态分布且价格路径的分析多集中在初始价格100左右这说明模拟结果出现极端数值的概率比较小。
在这里插入图片描述
在这里插入图片描述

2.Heston随机波动率

在Black-Scholes模型中最重要的简化假设之一便是波动率恒定不变。而在市场中波动率不是恒定不变的而是随着时间的变化而变化是具有随机性的。因此随机波动率过程的提出对之前的几何布朗运动进行了改进。
在这里插入图片描述
Heston模型的代码实现如下所示

# heston随机波动率
S0=100
r=0.05
v0=0.1
kappa=3
theta=0.25
sigma=0.1
rho=0.6
T=1
corr_mat=np.zeros((2,2))
corr_mat[0,:]=[1,rho]
corr_mat[1,:]=[rho,1]
cho_mat=np.linalg.cholesky(corr_mat)
cho_mat

M=50
I=10000
dt=T/M
ran_num=npr.standard_normal((2,M+1,I))
v=np.zeros_like(ran_num[0])
vh=np.zeros_like(v)
v[0]=v0
vh[0]=v0
for t in range(1,M+1):
    ran=np.dot(cho_mat,ran_num[:,t,:])
    vh[t]=(vh[t-1]+kappa*(theta-np.maximum(vh[t-1],0))*dt+sigma*np.sqrt(np.maximum(vh[t-1],0))*np.sqrt(dt)*ran[1])
v=np.maximum(vh,0)
S=np.zeros_like(ran_num[0])
S[0]=S0
for t in range(1,M+1):
    ran=np.dot(cho_mat,ran_num[:,t,:])
    S[t]=S[t-1]*np.exp((r-0.5*v[t])*dt+np.sqrt(v[t])*ran[0]*np.sqrt(dt))
fig,(ax1,ax2)=plt.subplots(1,2,figsize=(10,6))
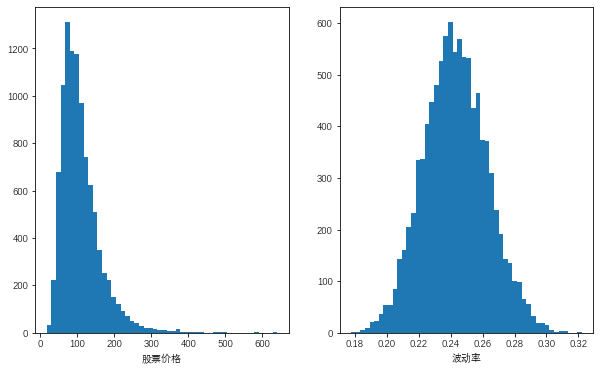
ax1.hist(S[-1],bins=50)
ax1.set_xlabel('股票价格')

ax2.hist(v[-1],bins=50)
ax2.set_xlabel('波动率')

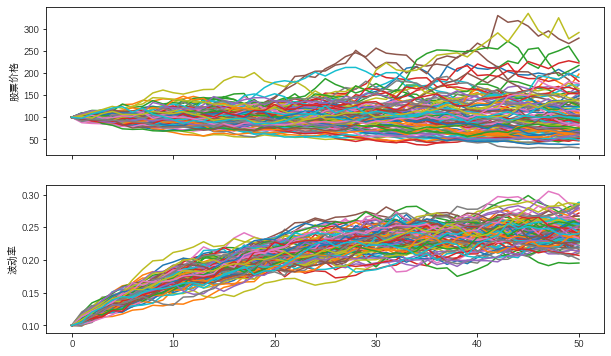
fig,(ax1,ax2)=plt.subplots(2,1,sharex=True,
                          figsize=(10,6))
ax1.plot(S[:,:100],lw=1.5)
ax1.set_ylabel('股票价格')
ax2.plot(v[:,:100],lw=1.5)
ax2.set_ylabel('波动率')

从图中可以看出Heston随机波动率模型对价格路径的模型情况相比于几何布朗运动而言呈现出明显的波动性特征且波动率过程的平均飘移值收敛于0.25θ数值。

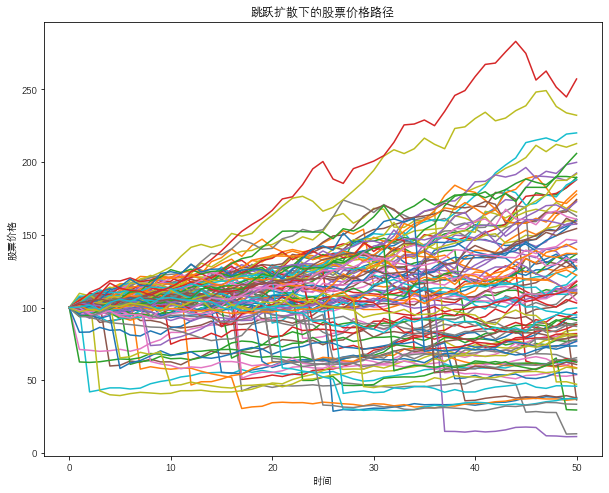
在这里插入图片描述
在这里插入图片描述

3.Merton跳跃-扩散

随机波动率和杠杆效应是许多市场中的典型现象。在市场交易中标的资产价格往往会因为突发事件而发生突然的跳跃。
1976年Merton提出了跳跃-扩散模型来模拟标的资产价格的路径。

Merton 模型假设标的资产价格的变化路径服从跳跃扩散过程。其中标的资产的价格变化过程中的跳跃部分属于可分散风险具有系统性风险的标的资产价格变化用几何布朗运动描述非系统性风险的标的资产价格跳跃用泊松跳跃过程描述跳跃的幅度则用正态分布表示。
在这里插入图片描述
Merton跳跃-扩散模型的代码实现为

# 跳跃扩散
S0=100
r=0.05
sigma=0.2
lamb=0.75
mu=-0.6
delta=0.25
rj=lamb*(math.exp(mu+0.5*delta**2)-1)
T=1
M=50
I=10000
dt=T/M
S=np.zeros((M+1,I))
S[0]=S0
sn1=npr.standard_normal((M+1,I))
sn2=npr.standard_normal((M+1,I))
poi=npr.poisson(lamb*dt,(M+1,I))
for t in range(1,M+1,1):
    S[t]=S[t-1]*(np.exp((r-rj-0.5*sigma**2)*dt+sigma*np.sqrt(dt)*sn1[t])+(np.exp(mu+delta*sn2[t])-1)*poi[t])
    S[t]=np.maximum(S[t],0)
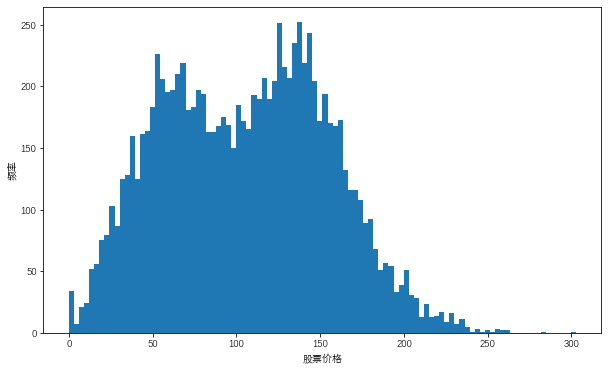
plt.figure(figsize=(10,6))
plt.hist(S[-1],bins=100)
plt.ylabel('频率')
plt.xlabel('股票价格')

从图中可以看出Merton模型对价格路径的模型呈现出明显的跳跃特征这表明在价格方程中加入跳跃因子以后对价格的模拟更加贴合实际市场。

在这里插入图片描述
在这里插入图片描述

三、三种随机过程下的蒙特卡洛模拟

金融期权表示在规定行权期日期欧式期权 或者规定时期美式期权内以规定价格所谓行权价 购买看涨期权 或者出售看跌期权 指定金融工具。这里我们考虑估值较为简单的情况——欧式期权。

基于某种指数的欧式看涨期权到期日收益通过公式h (ST )≡max(ST -K ,0)得出其中ST 是到期日T 的指数水平K 是行权价格。

给定相关随机过程例如几何布朗运动、Heston随机波动率模型、Merton跳跃-扩散模型等的风险中立测度或者在一个完备市场中这种权证的价格为
在这里插入图片描述

1.几何布朗运动下的蒙特卡洛模拟

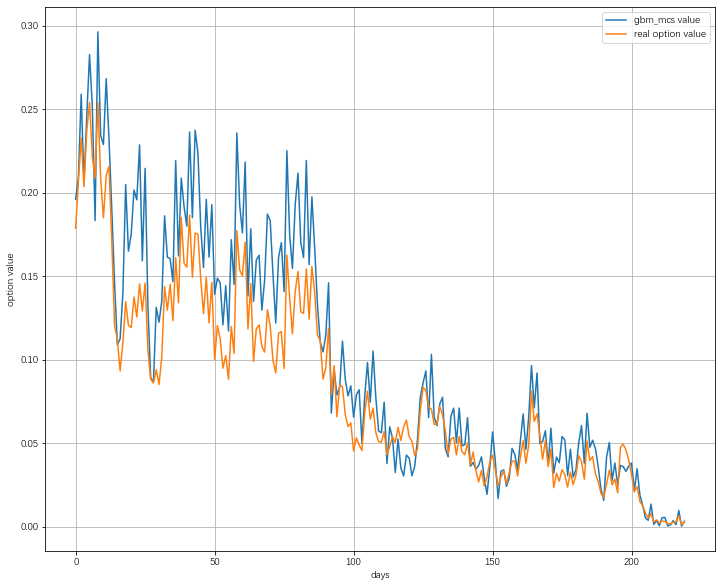
在前文中讲到蒙特卡洛模拟需要使用随机过程来模拟标的资产价格的变化路径首先采用几何布朗运动来模拟价格路径代码实现在前文中已给出。

几何布朗运动的蒙特卡洛模拟实现过程如下所示

# 几何布朗运动的随机过程下的蒙特卡洛模拟
S0=100
r=0.05
sigma=0.25
T=1
I=50000
M=50
def gbm_mcs_dyna(K,T,S0,option='call'):
    dt=T/M
    S=np.zeros((M+1,I))
    S[0]=S0
    sn=gen_sn(M,I)
    for t in range(1,M+1):
        S[t]=S[t-1]*np.exp((r-0.5*sigma**2)*dt+sigma*math.sqrt(dt)*sn[t])
    if option=='call':
        hT=np.maximum(S[-1]-K,0)
    else:
        hT=np.maximum(K-S[-1],0)
    C0=math.exp(-r*T)*np.mean(hT)
    return C0

和期权定价的数值方法之二叉树模型一样本文的数据采用沪深300期权。
【 期权定价的数值方法之二项式期权定价模型【附pyrhon代码】_xiaowu1997的博客-CSDN博客 https://blog.csdn.net/xiaowu1997/article/details/121730380】
数据一览
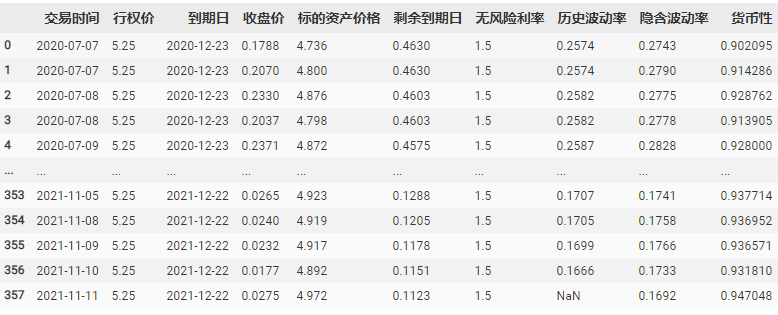
在这里插入图片描述
在这里插入图片描述

2.Heston随机波动率模型下的蒙特卡洛模拟

# heston随机波动率下的蒙特卡洛模拟
S0=100
r=0.015
v0=0.001
kappa=1.5
theta=0.25
sigma=0.25
rho=0.05
T=1
corr_mat=np.zeros((2,2))
corr_mat[0,:]=[1,rho]
corr_mat[1,:]=[rho,1]
cho_mat=np.linalg.cholesky(corr_mat)
cho_mat


M=50
I=50000
def heston_mcs_dyna(K,T,S0,option='call'):
    dt=T/M
    ran_num=npr.standard_normal((2,M+1,I))
    v=np.zeros_like(ran_num[0])
    vh=np.zeros_like(v)
    v[0]=v0
    vh[0]=v0
    for t in range(1,M+1):
        ran=np.dot(cho_mat,ran_num[:,t,:])
        vh[t]=(vh[t-1]+kappa*(theta-np.maximum(vh[t-1],0))*dt+sigma*np.sqrt(np.maximum(vh[t-1],0))*np.sqrt(dt)*ran[1])
    v=np.maximum(vh,0)
    S=np.zeros_like(ran_num[0])
    S[0]=S0
    for t in range(1,M+1):
        ran=np.dot(cho_mat,ran_num[:,t,:])
        S[t]=S[t-1]*np.exp((r-0.5*v[t])*dt+np.sqrt(v[t])*ran[0]*np.sqrt(dt))
    if option=='call':
        hT=np.maximum(S[-1]-K,0)
    else:
        hT=np.maximum(K-S[-1],0)
    C0=math.exp(-r*T)*np.mean(hT)
    return C0

结果如下所示
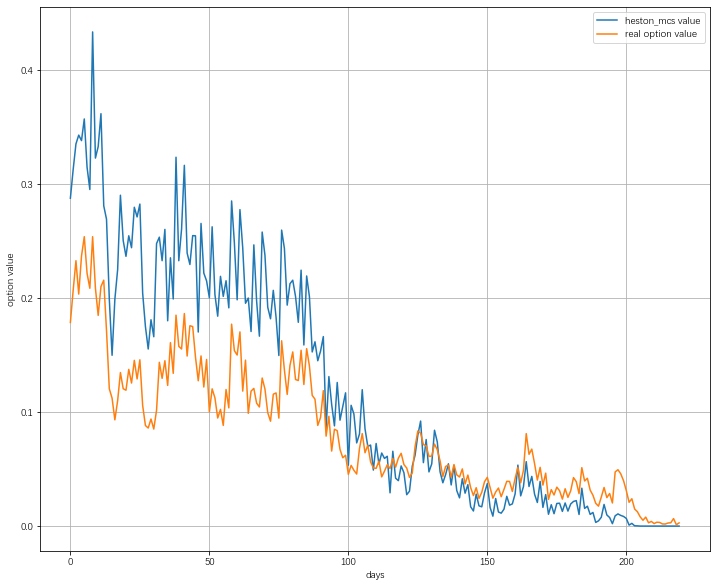
在这里插入图片描述

3.Merton跳跃-扩散模型下的蒙特卡洛模拟

# 跳跃扩散下的蒙特卡洛模拟
S0=100
r=0.015
sigma=0.15
lamb=0.25
mu=-0.45
delta=0.35
rj=lamb*(math.exp(mu+0.5*delta**2)-1)
T=1
def merton_mcs_dyna(K,T,S0,option='call'):
    M=50
    I=10000
    dt=T/M
    S=np.zeros((M+1,I))
    S[0]=S0
    sn1=npr.standard_normal((M+1,I))
    sn2=npr.standard_normal((M+1,I))
    poi=npr.poisson(lamb*dt,(M+1,I))
    for t in range(1,M+1,1):
        S[t]=S[t-1]*(np.exp((r-rj-0.5*sigma**2)*dt+sigma*np.sqrt(dt)*sn1[t])+(np.exp(mu+delta*sn2[t])-1)*poi[t])
        S[t]=np.maximum(S[t],0)
    if option=='call':
        hT=np.maximum(S[-1]-K,0)
    else:
        hT=np.maximum(K-S[-1],0)
    C0=math.exp(-r*T)*np.mean(hT)
    return C0

结果如下所示
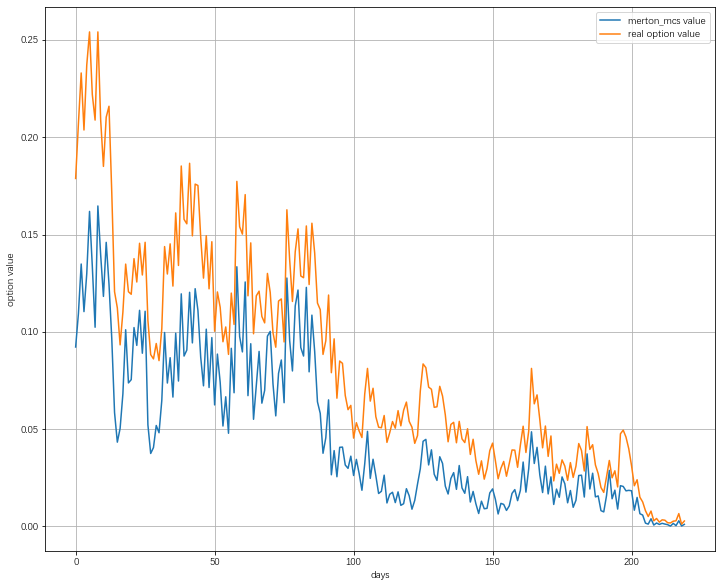
在这里插入图片描述
将三种随机过程下的蒙特卡洛模拟定价结果进行汇总可得
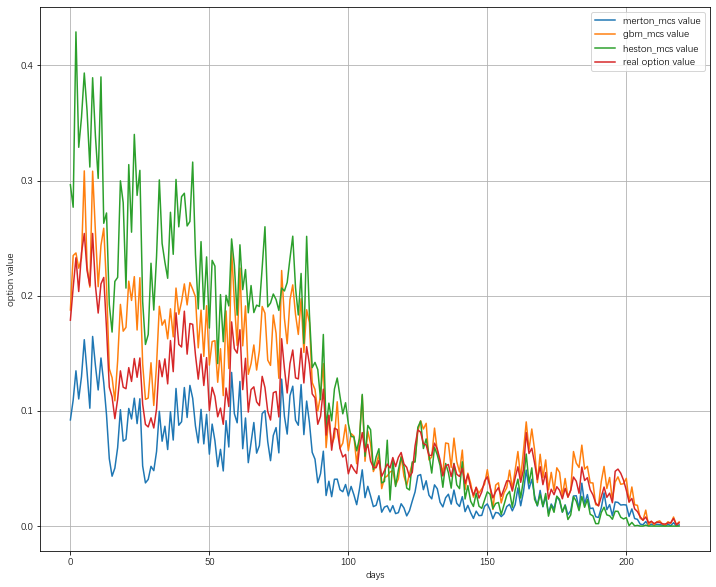
在这里插入图片描述
从图中可以看出Heston随机波动率模型下的蒙特卡洛模拟结果与期权真实数值偏离较大这是由于Heston模型的五个参数设置引起的实际上这五个参数的设置对模型的结果影响甚大因此在使用Heston随机波动率、Merton跳跃-扩散模型时模型的参数校准是很重要的参数设置如何直接影响到模型定价效果。

最后将三种随机过程下的蒙特卡洛模拟结果进行误差分析分析指标如下
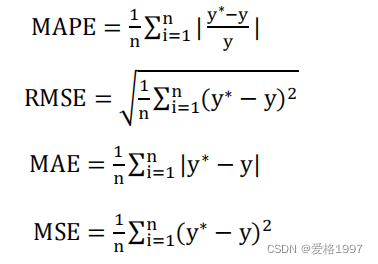
在这里插入图片描述

# mape
mape=np.mean(np.abs((pred-label)/label))
# rmse
rmse=np.sqrt(np.mean(np.square(pred-label)))
# mae
mae=np.mean(np.abs(pred-label))

#MSE
mse=np.sum((label-pred)**2)/len(pred)


MCS模型测试集的mape: 0.24558352558988158  rmse: 0.02772822093999324  mae: 0.020338912894752575 MSE: 0.0007688542364970798

MCS_heston模型测试集的mape: 0.5694931305822826  rmse: 0.0683480757390468  mae: 0.048791757486744324 MSE: 0.0046714594572304785

MCS_merton模型测试集的mape: 0.47548594626983554  rmse: 0.040602865373948735  mae: 0.034560276796007636 MSE: 0.001648592676575005

从指标中可以看出几何布朗运动下的蒙特卡洛模拟结果比heston随机波动率模型与merton跳跃扩散模型下的蒙特卡洛模拟结果要更加准确这也说明了对于heston模型与merton模型而言参数校准的重要性。

后续也会出一期关于heston模型与merton模型参数校准的博文。

总结

本章对蒙特卡洛模拟定价方法进行了简要的介绍并且对比了在三种不同的随机过程下的蒙特卡洛模拟定价结果。

如果对期权和期权定价有兴趣的话可以访问我写的期权机理与python量化的系统文章。
【期权机理与python实践】_xiaowu1997的博客-CSDN博客 https://blog.csdn.net/xiaowu1997/article/details/121478671

阿里云国内75折 回扣 微信号：monov8
阿里云国际，腾讯云国际，低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号：monov8 飞机：@monov6
标签: python
返回列表

上一篇：【算法笔记】三种背包问题——背包 DP

下一篇：含分布式电源的配电网可靠性评估研究（Matlab代码实现）

“期权定价数值方法之蒙特卡洛模拟【python量化】” 的相关文章

头歌-信息安全技术-用Python实现自己的区块链、支持以太坊的云笔记服务器端开发、编写并测试用于保存云笔记的智能合约、支持以太坊的云笔记小程序开发基础_头歌用什么技术开发的1年前 (2023-02-02)
2021：Python的下载安装教程（很详细，初学者也能懂）1年前 (2023-02-02)
我用Python做了个动图生成器，把一千个MM生成了GIF设置桌面，只为每天愉悦心情1年前 (2023-02-02)
python 如何使用 pandas 在 flask web 网页中分页显示 csv 文件数据1年前 (2023-02-02)
python删除目录下指定格式的所有文件1年前 (2023-02-02)
基于python知识图谱医疗领域问答系统实现（完整代码+数据可直接运行）1年前 (2023-02-02)
用Python的内置包Tkinter写一个练习系统2.01年前 (2023-02-02)
【阶段四】Python深度学习05篇：深度学习项目实战：卷积神经网络的定义、卷积网络的结构与卷积层的原理1年前 (2023-02-02)
Python经典编程习题100例：第31例：判断星期几1年前 (2023-02-02)
【阶段四】Python深度学习06篇：深度学习项目实战：卷积神经网络进行狗狗图像分类项目1年前 (2023-02-02)

阿里云国际版