使用Python从零实现多分类SVM-CSDN博客
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
本文将首先简要概述支持向量机及其训练和推理方程然后将其转换为代码以开发支持向量机模型。之后然后将其扩展成多分类的场景并通过使用Sci-kit Learn测试我们的模型来结束。
SVM概述
支持向量机的目标是拟合获得最大边缘的超平面(两个类中最近点的距离)。可以直观地表明这样的超平面(A)比没有最大化边际的超平面(B)具有更好的泛化特性和对噪声的鲁棒性。
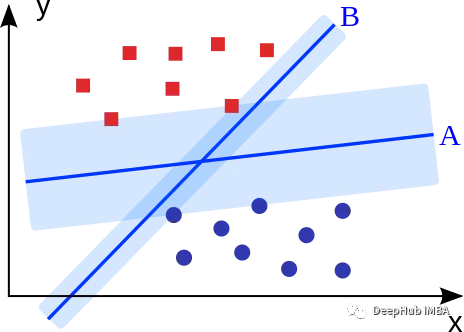
为了实现这一点SVM通过求解以下优化问题找到超平面的W和b:

它试图找到W,b使最近点的距离最大化并正确分类所有内容(如y取±1的约束)。这可以被证明相当于以下优化问题:

可以写出等价的对偶优化问题

这个问题的解决方案产生了一个拉格朗日乘数我们假设数据集中的每个点的大小为m:(α 1 α 2…α _n)。目标函数在α中明显是二次的约束是线性的这意味着它可以很容易地用二次规划求解。一旦找到解由对偶的推导可知:

注意只有具有α>0的点才定义超平面(对和有贡献)。这些被称为支持向量。因此当给定一个新例子x时返回其预测y=±1的预测方程为:
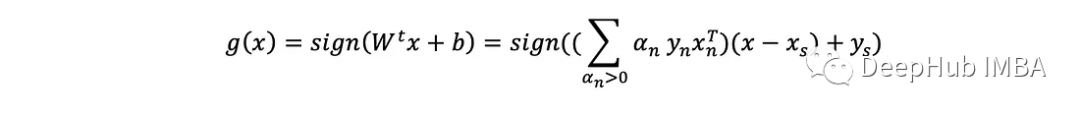
这种支持向量机的基本形式被称为硬边界支持向量机hard margin SVM因为它解决的优化问题(如上所述)强制要求训练中的所有点必须被正确分类。但在实际场景中可能存在一些噪声阻止或限制了完美分离数据的超平面在这种情况下优化问题将不返回或返回一个糟糕的解决方案。

软边界支持向量机soft margin SVM通过引入C常数(用户给定的超参数)来适应优化问题该常数控制它应该有多“硬”。特别地它将原优化问题修改为:

它允许每个点产生一些错误λ(例如在超平面的错误一侧)并且通过将它们在目标函数中的总和加权C来减少它们。当C趋于无穷时(一般情况下肯定不会)它就等于硬边界。与此同时较小的C将允许更多的“违规行为”(以换取更大的支持;例如更小的w (w)。
可以证明等价对偶问题只有在约束每个点的α≤C时才会发生变化。

由于允许违例支持向量(带有α>0的点)不再都在边界的边缘。任何错误的支持向量都具有α=C而非支持向量(α=0)不能发生错误。我们称潜在错误(α=C)的支持向量为“非错误编剧支持向量”和其他纯粹的支持向量(没有违规;“边界支持向量”(0<α<C)。
这样推理方程不变:
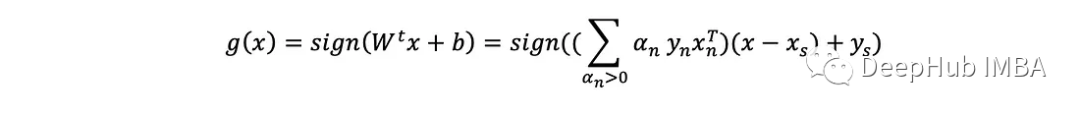
现在(xₛyₛ)必须是一个没有违规的支持向量因为方程假设它在边界的边缘。
软边界支持向量机扩展了硬边界支持向量机来处理噪声但通常由于噪声以外的因素例如自然非线性数据不能被超平面分离。软边界支持向量机可以用于这样的情况但是最优解决方案的超平面它允许的误差远远超过现实中可以容忍的误差。
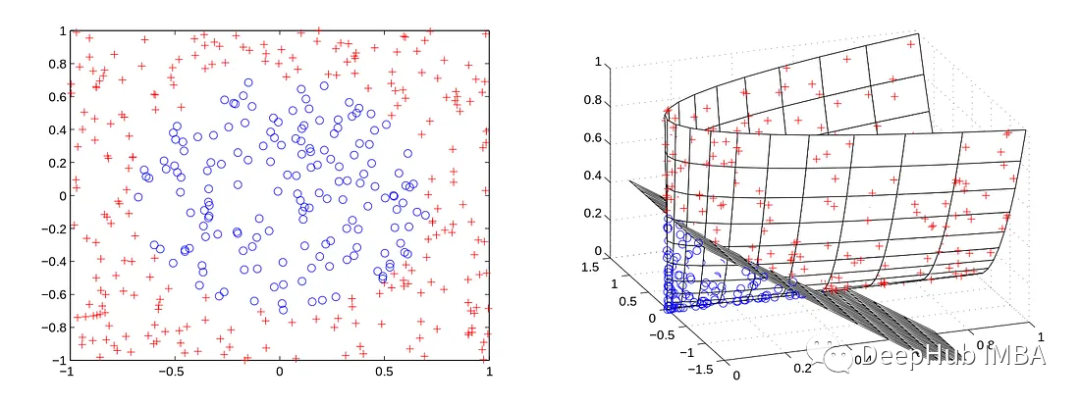
例如在左边的例子中无论C的设置如何软边界支持向量机都找不到线性超平面。但是可以通过某种转换函数z=Φ(x)将数据集中的每个点x映射到更高的维度从而使数据在新的高维空间中更加线性(或完全线性)。这相当于用z替换x得到:

在现实中特别是当Φ转换为非常高维的空间时计算z可能需要很长时间。所以就出现了核函数。它用一个数学函数(称为核函数)的等效计算来取代z并且更快(例如对z进行代数简化)。例如这里有一些流行的核函数(每个都对应于一些转换Φ到更高维度空间):
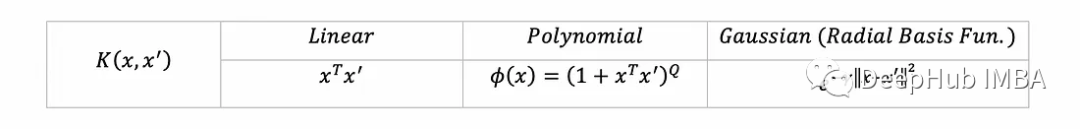
这样对偶优化问题就变成:
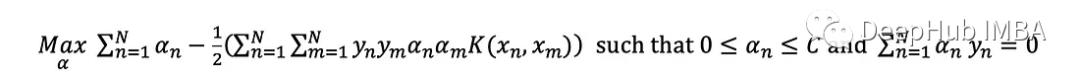
直观地推理方程(经过代数处理后)为:

上面所有方程的完整推导有很多相关的文章了我们就不详细介绍了。
Python实现
对于实现我们将使用下面这些库
import numpy as np # for basic operations over arrays
from scipy.spatial import distance # to compute the Gaussian kernel
import cvxopt # to solve the dual opt. problem
import copy # to copy numpy arrays
定义核和SVM超参数我们将实现常见的三个核函数
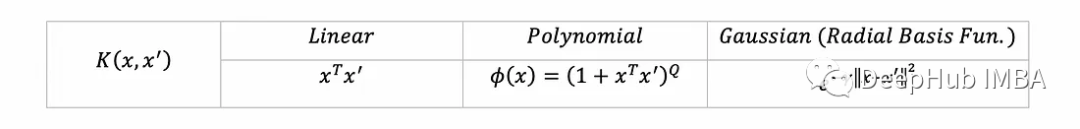
class SVM:
linear = lambda x, xࠤ , c=0: x @ xࠤ.T
polynomial = lambda x, xࠤ , Q=5: (1 + x @ xࠤ.T)**Q
rbf = lambda x, xࠤ, γ=10: np.exp(-γ*distance.cdist(x, xࠤ,'sqeuclidean'))
kernel_funs = {'linear': linear, 'polynomial': polynomial, 'rbf': rbf}
为了与其他核保持一致线性核采用了一个额外的无用的超参数。kernel_funs接受核函数名称的字符串并返回相应的内核函数。
继续定义构造函数:
class SVM:
linear = lambda x, xࠤ , c=0: x @ xࠤ.T
polynomial = lambda x, xࠤ , Q=5: (1 + x @ xࠤ.T)**Q
rbf = lambda x, xࠤ, γ=10: np.exp(-γ*distance.cdist(x, xࠤ,'sqeuclidean'))
kernel_funs = {'linear': linear, 'polynomial': polynomial, 'rbf': rbf}
def __init__(self, kernel='rbf', C=1, k=2):
# set the hyperparameters
self.kernel_str = kernel
self.kernel = SVM.kernel_funs[kernel]
self.C = C # regularization parameter
self.k = k # kernel parameter
# training data and support vectors (set later)
self.X, y = None, None
self.αs = None
# for multi-class classification (set later)
self.multiclass = False
self.clfs = []
SVM有三个主要的超参数核(我们存储给定的字符串和相应的核函数)正则化参数C和核超参数(传递给核函数);它表示多项式核的Q和RBF核的γ。
为了兼容sklearn的形式我们需要使用fit和predict函数来扩展这个类定义以下函数并在稍后将其用作装饰器:
SVMClass = lambda func: setattr(SVM, func.__name__, func) or func
拟合SVM对应于通过求解对偶优化问题找到每个点的支持向量α:
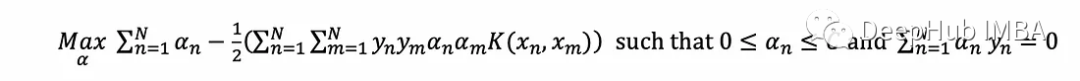
设α为可变列向量(α₁α₂…α _n);y为标签(y₁α₂…y_N)常数列向量;K为常数矩阵其中K[n,m]计算核在(x, x)处的值。点积、外积和二次型分别基于索引的等价表达式:
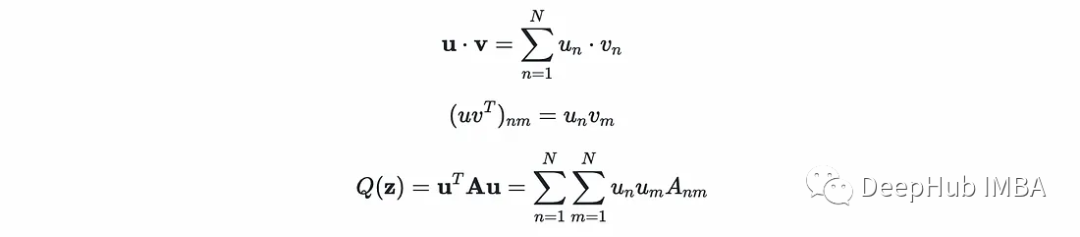
可以将对偶优化问题写成矩阵形式如下:
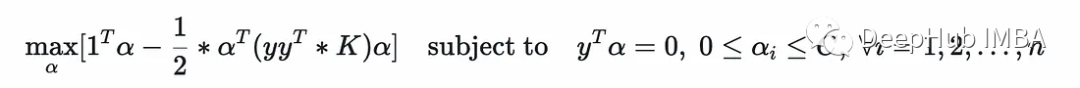
这是一个二次规划CVXOPT的文档中解释如下:

可以只使用(P,q)或(P,q,G,h)或(P,q,G,h, A, b)等等来调用它(任何未给出的都将由默认值设置例如1)。
对于(P, q, G, h, A, b)的值我们的例子可以做以下比较:

为了便于比较将第一个重写如下:
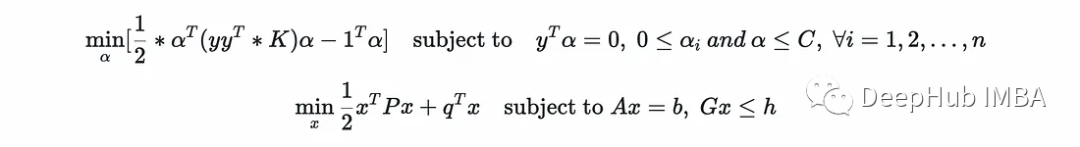
现在很明显(0≤α等价于-α≤0):

我们就可以写出如下的fit函数:
@SVMClass
def fit(self, X, y, eval_train=False):
# if more than two unique labels, call the multiclass version
if len(np.unique(y)) > 2:
self.multiclass = True
return self.multi_fit(X, y, eval_train)
# if labels given in {0,1} change it to {-1,1}
if set(np.unique(y)) == {0, 1}: y[y == 0] = -1
# ensure y is a Nx1 column vector (needed by CVXOPT)
self.y = y.reshape(-1, 1).astype(np.double) # Has to be a column vector
self.X = X
N = X.shape[0] # Number of points
# compute the kernel over all possible pairs of (x, x') in the data
# by Numpy's vectorization this yields the matrix K
self.K = self.kernel(X, X, self.k)
### Set up optimization parameters
# For 1/2 x^T P x + q^T x
P = cvxopt.matrix(self.y @ self.y.T * self.K)
q = cvxopt.matrix(-np.ones((N, 1)))
# For Ax = b
A = cvxopt.matrix(self.y.T)
b = cvxopt.matrix(np.zeros(1))
# For Gx <= h
G = cvxopt.matrix(np.vstack((-np.identity(N),
np.identity(N))))
h = cvxopt.matrix(np.vstack((np.zeros((N,1)),
np.ones((N,1)) * self.C)))
# Solve
cvxopt.solvers.options['show_progress'] = False
sol = cvxopt.solvers.qp(P, q, G, h, A, b)
self.αs = np.array(sol["x"]) # our solution
# a Boolean array that flags points which are support vectors
self.is_sv = ((self.αs-1e-3 > 0)&(self.αs <= self.C)).squeeze()
# an index of some margin support vector
self.margin_sv = np.argmax((0 < self.αs-1e-3)&(self.αs < self.C-1e-3))
if eval_train:
print(f"Finished training with accuracy{self.evaluate(X, y)}")
我们确保这是一个二进制问题并且二进制标签按照支持向量机(±1)的假设设置并且y是一个维数为(N,1)的列向量。然后求解求解(α₁α₂…α _n) 的优化问题。
使用(α₁α₂…α _n) _来获得在与支持向量对应的任何索引处为1的标志数组然后可以通过仅对支持向量和(xₛyₛ)的边界支持向量的索引求和来应用预测方程。我们确实假设非支持向量可能不完全具有α=0如果它的α≤1e-3那么这是近似为零(CVXOPT结果可能不是最终精确的)。同样假设非边际支持向量可能不完全具有α=C。
下面就是预测的方法预测方程为:
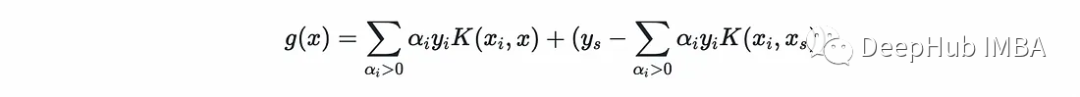
@SVMClass
def predict(self, X_t):
if self.multiclass: return self.multi_predict(X_t)
# compute (xₛ, yₛ)
xₛ, yₛ = self.X[self.margin_sv, np.newaxis], self.y[self.margin_sv]
# find support vectors
αs, y, X= self.αs[self.is_sv], self.y[self.is_sv], self.X[self.is_sv]
# compute the second term
b = yₛ - np.sum(αs * y * self.kernel(X, xₛ, self.k), axis=0)
# compute the score
score = np.sum(αs * y * self.kernel(X, X_t, self.k), axis=0) + b
return np.sign(score).astype(int), score
我们还可以实现一个评估方法来计算精度(在上面的fit中使用)。
@SVMClass
def evaluate(self, X,y):
outputs, _ = self.predict(X)
accuracy = np.sum(outputs == y) / len(y)
return round(accuracy, 2)
最后测试我们的完整代码
from sklearn.datasets import make_classification
import numpy as np
# Load the dataset
np.random.seed(1)
X, y = make_classification(n_samples=2500, n_features=5,
n_redundant=0, n_informative=5,
n_classes=2, class_sep=0.3)
# Test Implemented SVM
svm = SVM(kernel='rbf', k=1)
svm.fit(X, y, eval_train=True)
y_pred, _ = svm.predict(X)
print(f"Accuracy: {np.sum(y==y_pred)/y.shape[0]}") #0.9108
# Test with Scikit
from sklearn.svm import SVC
clf = SVC(kernel='rbf', C=1, gamma=1)
clf.fit(X, y)
y_pred = clf.predict(X)
print(f"Accuracy: {sum(y==y_pred)/y.shape[0]}") #0.9108
多分类SVM
我们都知道SVM的目标是二元分类如果要将模型推广到多类则需要为每个类训练一个二元SVM分类器然后对每个类进行循环并将属于它的点重新标记为+1并将所有其他类的点重新标记为-1。
当给定k个类时训练的结果是k个分类器其中第i个分类器在数据上进行训练第i个分类器被标记为+1所有其他分类器被标记为-1。
@SVMClass
def multi_fit(self, X, y, eval_train=False):
self.k = len(np.unique(y)) # number of classes
# for each pair of classes
for i in range(self.k):
# get the data for the pair
Xs, Ys = X, copy.copy(y)
# change the labels to -1 and 1
Ys[Ys!=i], Ys[Ys==i] = -1, +1
# fit the classifier
clf = SVM(kernel=self.kernel_str, C=self.C, k=self.k)
clf.fit(Xs, Ys)
# save the classifier
self.clfs.append(clf)
if eval_train:
print(f"Finished training with accuracy {self.evaluate(X, y)}")
然后为了对新示例执行预测我们选择相应分类器最自信(得分最高)的类。
@SVMClass
def multi_predict(self, X):
# get the predictions from all classifiers
N = X.shape[0]
preds = np.zeros((N, self.k))
for i, clf in enumerate(self.clfs):
_, preds[:, i] = clf.predict(X)
# get the argmax and the corresponding score
return np.argmax(preds, axis=1), np.max(preds, axis=1)
完整测试代码
from sklearn.datasets import make_classification
import numpy as np
# Load the dataset
np.random.seed(1)
X, y = make_classification(n_samples=500, n_features=2,
n_redundant=0, n_informative=2,
n_classes=4, n_clusters_per_class=1,
class_sep=0.3)
# Test SVM
svm = SVM(kernel='rbf', k=4)
svm.fit(X, y, eval_train=True)
y_pred = svm.predict(X)
print(f"Accuracy: {np.sum(y==y_pred)/y.shape[0]}") # 0.65
# Test with Scikit
from sklearn.multiclass import OneVsRestClassifier
from sklearn.svm import SVC
clf = OneVsRestClassifier(SVC(kernel='rbf', C=1, gamma=4)).fit(X, y)
y_pred = clf.predict(X)
print(f"Accuracy: {sum(y==y_pred)/y.shape[0]}") # 0.65
绘制每个决策区域的图示得到以下图:
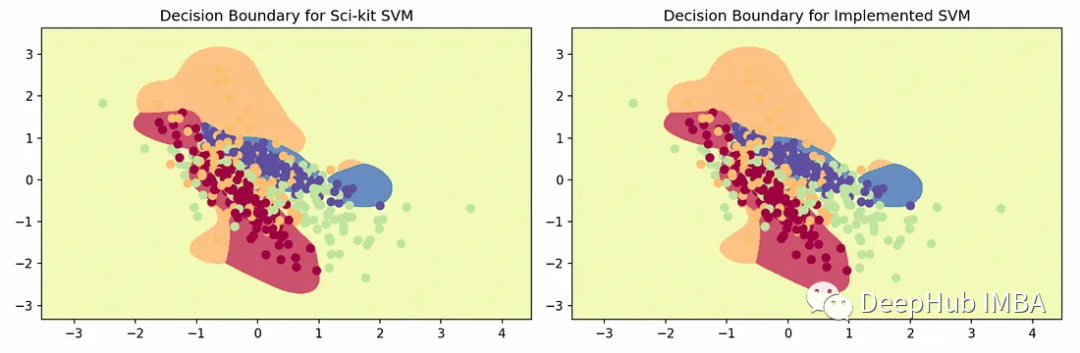
可以看到我们的实现与Sci-kit Learn结果相当说明在算法实现上没有问题。注意SVM默认支持OVR(没有如上所示的显式调用)它是特定于SVM的进一步优化。
总结
我们使用Python实现了支持向量机(SVM)学习算法并且包括了软边界和常用的三个核函数。我们还将SVM扩展到多分类的场景并使用Sci-kit Learn验证了我们的实现。希望通过本文你可以更好的了解SVM。
https://avoid.overfit.cn/post/0b2410e6737a4911be507ca29cb3136c
作者Essam Wisam
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

