【Python数据科学快速入门系列 | 04】Numpy四则运算、矩阵运算和广播机制的爱恨情仇
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
这是机器未来的第43篇文章
原文首发地址https://blog.csdn.net/RobotFutures/article/details/126493989

文章目录
1. 概述
本文总结了numpy常见的运算四则运算与矩阵运算以及它们的区别。同时描述了在形状不满足要求时在特定情况下仍然可以运算的广播机制。
2. 四则运算
四则运算即是小学时学过的+、-、*、/在numpy中ndarray数组对象怎么进行四则运算呢
四则运算都是对位运算数学公式如下
# 生成2个3*3数组
import numpy as np
a = np.random.randint(low=1,high=100,size=(3,3))
b = np.random.randint(low=1,high=100,size=(3,3))
print(f"a:\n{a}, type:{type(a)}")
print(f"b:\n{b}")
a:
[[84 16 27]
[39 33 87]
[82 16 37]], type:<class 'numpy.ndarray'>
b:
[[68 33 96]
[92 43 69]
[14 4 88]]
2.1 加法
s u m = ∑ i , j M , N ( a i j + b i j ) sum = \sum_{i, j}^{M,N}(a_{ij}+b_{ij}) sum=i,j∑M,N(aij+bij)
# 加法
sum = a + b
print(f"sum:\n{sum}")
sum:
[[128 154 172]
[ 79 133 16]
[ 96 39 115]]
2.2 减法
d i f f = ∑ i , j M , N ( a i j − b i j ) diff = \sum_{i, j}^{M,N}(a_{ij}-b_{ij}) diff=i,j∑M,N(aij−bij)
# 减法
diff = a - b
print(f"diff:\n{diff}")
diff:
[[-30 2 -26]
[ 13 1 -6]
[-18 -3 21]]
2.3 乘法
p r o d u c t = ∑ i , j M , N ( a i j ∗ b i j ) product = \sum_{i, j}^{M,N}(a_{ij}*b_{ij}) product=i,j∑M,N(aij∗bij)
# 乘法
product = a * b
print(f"product:\n{product}")
product:
[[3871 5928 7227]
[1518 4422 55]
[2223 378 3196]]
2.4 除法
q u o t i e n t = ∑ i , j M , N ( a i j / b i j ) quotient = \sum_{i, j}^{M,N}(a_{ij}/b_{ij}) quotient=i,j∑M,N(aij/bij)
# 除法
quotient = a / b
print(f"quotient:\n{quotient}")
quotient:
[[0.62025316 1.02631579 0.73737374]
[1.39393939 1.01515152 0.45454545]
[0.68421053 0.85714286 1.44680851]]
3. 矩阵运算
上面描述了ndarray数组对象的四则运算如何利用numpy进行矩阵运算呢
矩阵运算基本运算为加、减、乘法及数乘。
矩阵的加法、减法运算和数组的加法、减法运算一样都是对位运算数乘运算也比较简单就是每个元素都乘以数但是矩阵乘法和数组的乘法差距较大。
假设有两个矩阵, MxN矩阵A和NxS矩阵B, 两个矩阵矩阵相乘后结果为MxS矩阵。
矩阵A的列和矩阵B的行必须相等才可以进行矩阵运算。
假设矩阵A为4*3的矩阵矩阵B为3*2的矩阵
矩阵A
[
a
0
,
0
a
0
,
1
a
0
,
2
a
1
,
0
a
1
,
1
a
1
,
2
a
2
,
0
a
2
,
1
a
2
,
2
a
3
,
0
a
3
,
1
a
3
,
2
]
\begin{bmatrix} a_{0,0} & a_{0,1} & a_{0,2} \\ a_{1,0} & a_{1,1} & a_{1,2} \\ a_{2,0} & a_{2,1} & a_{2,2} \\ a_{3,0} & a_{3,1} & a_{3,2} \end{bmatrix}
⎣
⎡a0,0a1,0a2,0a3,0a0,1a1,1a2,1a3,1a0,2a1,2a2,2a3,2⎦
⎤
矩阵B
[
b
0
,
0
b
0
,
1
b
1
,
0
b
1
,
1
b
2
,
0
b
2
,
1
]
\begin{bmatrix} b_{0,0} & b_{0,1} \\ b_{1,0} & b_{1,1} \\ b_{2,0} & b_{2,1} \\ \end{bmatrix}
⎣
⎡b0,0b1,0b2,0b0,1b1,1b2,1⎦
⎤
矩阵A乘以矩阵B的结果4*2的矩阵
[
a
0
,
0
∗
b
0
,
0
+
a
0
,
1
∗
b
1
,
0
+
a
0
,
2
∗
b
2
,
0
a
0
,
0
∗
b
0
,
1
+
a
0
,
1
∗
b
1
,
1
+
a
0
,
2
∗
b
2
,
1
a
1
,
0
∗
b
0
,
0
+
a
1
,
1
∗
b
1
,
0
+
a
1
,
2
∗
b
2
,
0
a
1
,
0
∗
b
0
,
1
+
a
1
,
1
∗
b
1
,
1
+
a
1
,
2
∗
b
2
,
1
a
2
,
0
∗
b
0
,
0
+
a
2
,
1
∗
b
1
,
0
+
a
2
,
2
∗
b
2
,
0
a
2
,
0
∗
b
0
,
1
+
a
2
,
1
∗
b
1
,
1
+
a
2
,
2
∗
b
2
,
1
a
3
,
0
∗
b
0
,
0
+
a
3
,
1
∗
b
1
,
0
+
a
3
,
2
∗
b
2
,
0
a
3
,
0
∗
b
0
,
1
+
a
3
,
1
∗
b
1
,
1
+
a
3
,
2
∗
b
2
,
1
]
\begin{bmatrix} a_{0,0}*b_{0,0}+a_{0,1}*b_{1,0}+a_{0,2}*b_{2,0} & a_{0,0}*b_{0, 1}+a_{0,1}*b_{1,1}+ a_{0,2} *b_{2,1}\\ a_{1,0}*b_{0,0}+a_{1,1}*b_{1,0}+a_{1,2}*b_{2,0} & a_{1,0}*b_{0, 1}+a_{1,1}*b_{1,1}+ a_{1,2} *b_{2,1}\\ a_{2,0}*b_{0,0}+a_{2,1}*b_{1,0}+a_{2,2}*b_{2,0} & a_{2,0}*b_{0, 1}+a_{2,1}*b_{1,1}+ a_{2,2} *b_{2,1}\\ a_{3,0}*b_{0,0}+a_{3,1}*b_{1,0}+a_{3,2}*b_{2,0} & a_{3,0}*b_{0, 1}+a_{3,1}*b_{1,1}+ a_{3,2} *b_{2,1}\\ \end{bmatrix}
⎣
⎡a0,0∗b0,0+a0,1∗b1,0+a0,2∗b2,0a1,0∗b0,0+a1,1∗b1,0+a1,2∗b2,0a2,0∗b0,0+a2,1∗b1,0+a2,2∗b2,0a3,0∗b0,0+a3,1∗b1,0+a3,2∗b2,0a0,0∗b0,1+a0,1∗b1,1+a0,2∗b2,1a1,0∗b0,1+a1,1∗b1,1+a1,2∗b2,1a2,0∗b0,1+a2,1∗b1,1+a2,2∗b2,1a3,0∗b0,1+a3,1∗b1,1+a3,2∗b2,1⎦
⎤
矩阵相乘的计算过程为
矩阵A和第k行和矩阵B的第k列相乘矩阵A的第k行第i列的元素乘以矩阵B第j列第i行的元素然后它们的乘积再想加就是结果的第ij元素。
C
i
,
j
=
a
i
,
0
∗
b
0
,
j
+
a
i
,
1
∗
b
1
,
j
+
.
.
.
+
a
i
,
n
∗
b
n
,
j
=
∑
k
=
0
n
a
i
k
b
k
j
C_{i,j} = a_{i,0}*b_{0,j}+a_{i,1}*b_{1,j}+...+a_{i,n}*b_{n,j} = \sum_{k=0}^{n}a_{ik}b_{kj}
Ci,j=ai,0∗b0,j+ai,1∗b1,j+...+ai,n∗bn,j=k=0∑naikbkj
矩阵乘法也叫求矩阵的内积是深度学习神经网络最底层的数学基础。
numpy中计算矩阵乘法的方式有4种
3.1 np.dot函数
arr_a = np.array([[1,2,3],[4, 5, 6], [7, 8, 9], [1, 2, 3]])
arr_b = np.array([[1, 1], [2, 2], [3, 3]])
print(f"arr_a:{arr_a.shape},{type(arr_a)}\n{arr_a}")
print(f"arr_b:{arr_b.shape},{type(arr_b)}\n{arr_b}")
matrix_c = np.dot(arr_a, arr_b)
print(f"matrix_c:{matrix_c.shape},{type(matrix_c)}\n{matrix_c}")
arr_a:(4, 3),<class 'numpy.ndarray'>
[[1 2 3]
[4 5 6]
[7 8 9]
[1 2 3]]
arr_b:(3, 2),<class 'numpy.ndarray'>
[[1 1]
[2 2]
[3 3]]
matrix_c:(4, 2),<class 'numpy.ndarray'>
[[14 14]
[32 32]
[50 50]
[14 14]]
3.2 np.matmul函数
从numpy1.10.0开始支持。
arr_a = np.array([[1,2,3],[4, 5, 6], [7, 8, 9], [1, 2, 3]])
arr_b = np.array([[1, 1], [2, 2], [3, 3]])
print(f"arr_a:{arr_a.shape},{type(arr_a)}\n{arr_a}")
print(f"arr_b:{arr_b.shape},{type(arr_b)}\n{arr_b}")
matrix_c = np.matmul(arr_a, arr_b)
print(f"matrix_c:{matrix_c.shape},{type(matrix_c)}\n{matrix_c}")
arr_a:(4, 3),<class 'numpy.ndarray'>
[[1 2 3]
[4 5 6]
[7 8 9]
[1 2 3]]
arr_b:(3, 2),<class 'numpy.ndarray'>
[[1 1]
[2 2]
[3 3]]
matrix_c:(4, 2),<class 'numpy.ndarray'>
[[14 14]
[32 32]
[50 50]
[14 14]]
3.3 @运算符
arr_a = np.array([[1,2,3],[4, 5, 6], [7, 8, 9], [1, 2, 3]])
arr_b = np.array([[1, 1], [2, 2], [3, 3]])
print(f"arr_a:{arr_a.shape},{type(arr_a)}\n{arr_a}")
print(f"arr_b:{arr_b.shape},{type(arr_b)}\n{arr_b}")
matrix_c = arr_a @ arr_b
print(f"matrix_c:{matrix_c.shape},{type(matrix_c)}\n{matrix_c}")
arr_a:(4, 3),<class 'numpy.ndarray'>
[[1 2 3]
[4 5 6]
[7 8 9]
[1 2 3]]
arr_b:(3, 2),<class 'numpy.ndarray'>
[[1 1]
[2 2]
[3 3]]
matrix_c:(4, 2),<class 'numpy.ndarray'>
[[14 14]
[32 32]
[50 50]
[14 14]]
3.4 转换为矩阵再运算
利用np.asmatrix方法
arr_a = np.array([[1,2,3],[4, 5, 6], [7, 8, 9], [1, 2, 3]])
arr_b = np.array([[1, 1], [2, 2], [3, 3]])
print(f"arr_a:{arr_a.shape},{type(arr_a)}\n{arr_a}")
print(f"arr_b:{arr_b.shape},{type(arr_b)}\n{arr_b}")
# np.matrix方法已不推荐使用将来会移除asmatrix不会拷贝副本
matrix_c = np.asmatrix(arr_a) * np.asmatrix(arr_b)
print(f"matrix_c:{matrix_c.shape},{type(matrix_c)}\n{matrix_c}")
arr_a:(4, 3),<class 'numpy.ndarray'>
[[1 2 3]
[4 5 6]
[7 8 9]
[1 2 3]]
arr_b:(3, 2),<class 'numpy.ndarray'>
[[1 1]
[2 2]
[3 3]]
matrix_c:(4, 2),<class 'numpy.matrix'>
[[14 14]
[32 32]
[50 50]
[14 14]]
4. numpy的广播机制
Numpy的四则运算在计算时必须满足形状一致而Numpy的广播机制在满足广播条件约束的情况可以将不同形状的数组扩展成统一的形状然后再进行运算。
一般广播规则
当对两个数组进行操作时NumPy 会逐元素比较它们的形状。 它从尾随即最右边维度开始从右向左比较
(1)维度不相等两个数组的右侧轴元素个数相符
(2)维度相等且其中之一的轴的元素个数为1且其它轴的元素个数相等
(3)维度不相等两个数组的右侧元素个数不相符且一侧元素个数为1则按照两侧元素个数多的为标准进行广播
则满足广播机制。
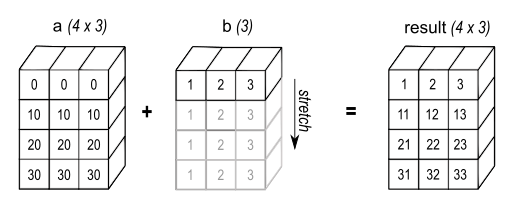
4.1 举例1
数组a,其形状为4*3数组b其形状为3,从尾部开始比较数组a的形状4*3包含数组b的形状3因此满足广播机制。
import numpy as np
a = np.array([[ 0.0, 0.0, 0.0],
[10.0, 10.0, 10.0],
[20.0, 20.0, 20.0],
[30.0, 30.0, 30.0]])
b = np.array([1.0, 2.0, 3.0])
c = a + b
print(a.shape, b.shape, c.shape)
print(c)
(4, 3) (3,) (4, 3)
[[ 1. 2. 3.]
[11. 12. 13.]
[21. 22. 23.]
[31. 32. 33.]]
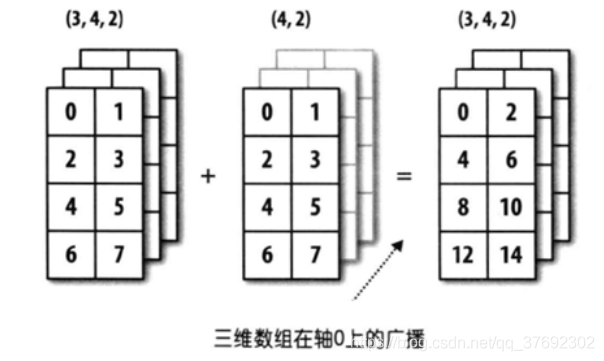
4.2 举例2
数组a,其形状为3*4*2数组b其形状为4*2,从尾部开始比较数组a的形状3*4*2包含数组b的形状4*2因此满足广播机制。
a = np.random.randint(low=0, high=10, size=(3, 4, 2))
b = np.random.randint(low=0, high=10, size=(4,2))
c = a + b
print(a.shape, b.shape, c.shape)
print(f"a:{a}\nb:{b}\nc:{c}")
(3, 4, 2) (4, 2) (3, 4, 2)
a:[[[6 0]
[2 3]
[7 6]
[9 7]]
[[3 1]
[0 5]
[6 0]
[1 9]]
[[7 2]
[0 3]
[2 3]
[0 6]]]
b:[[7 3]
[0 5]
[6 7]
[1 7]]
c:[[[13 3]
[ 2 8]
[13 13]
[10 14]]
[[10 4]
[ 0 10]
[12 7]
[ 2 16]]
[[14 5]
[ 0 8]
[ 8 10]
[ 1 13]]]
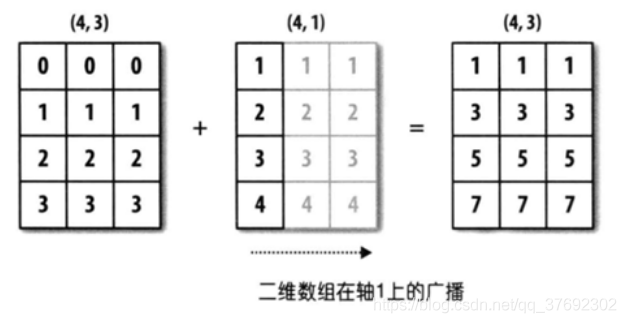
4.3 举例3
数组a形状为4*3,数组b形状为4*1数组维度相同有2个维度其中一个维度元素个数为1另外一个维度元素个数相等满足广播机制
import numpy as np
a = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]]) #arr1.shape = (4,3)
b = np.array([[1],[2],[3],[4]]) #arr2.shape = (4, 1)
c = a + b
print(c)
[[1 1 1]
[3 3 3]
[5 5 5]
[7 7 7]]
4.4 举例4
数组a形状为(5, 4, 3),数组b形状为(5, 1, 3)数组维度相同有3个维度其中一个维度元素个数为1另外2个维度元素个数相等满足广播机制
a = np.random.randint(low=0, high=10, size=(5, 4, 3))
b = np.random.randint(low=0, high=10, size=(5, 1, 3))
c = a + b
print(a.shape, b.shape, c.shape)
print(f"a:{a}\nb:{b}\nc:{c}")
(5, 4, 3) (5, 1, 3) (5, 4, 3)
a:[[[7 4 5]
[9 9 1]
[7 6 8]
[9 5 7]]
[[3 0 0]
[1 2 4]
[0 1 8]
[5 2 6]]
[[9 5 0]
[5 8 5]
[7 1 8]
[9 2 9]]
[[7 9 0]
[4 5 3]
[7 2 7]
[0 8 9]]
[[2 4 2]
[2 3 1]
[8 3 5]
[5 7 4]]]
b:[[[2 5 2]]
[[4 3 3]]
[[5 3 0]]
[[0 6 6]]
[[3 6 8]]]
c:[[[ 9 9 7]
[11 14 3]
[ 9 11 10]
[11 10 9]]
[[ 7 3 3]
[ 5 5 7]
[ 4 4 11]
[ 9 5 9]]
[[14 8 0]
[10 11 5]
[12 4 8]
[14 5 9]]
[[ 7 15 6]
[ 4 11 9]
[ 7 8 13]
[ 0 14 15]]
[[ 5 10 10]
[ 5 9 9]
[11 9 13]
[ 8 13 12]]]
4.5 举例5
数组a的形状为(3, 1, 2)数组b的形状为(4, 1)从右侧向左比较数组a和数组b的维度不相等右侧元素个数也不相等但是两侧都有出现轴的元素个数为1的情况则轴元素个数为1的维度根据两者的较大值进行广播。
从右向左比较数据b首先在第2维上广播为(4, 2)然后数组a在第1维广播为(3, 4, 2)数组b在第0维广播为(3, 4, 2)
a = np.random.randint(low=0, high=10, size=(3, 1, 2))
b = np.random.randint(low=0, high=10, size=(4, 1))
c = a + b
print(a.shape, b.shape, c.shape)
print(f"a:{a}\nb:{b}\nc:{c}")
(3, 1, 2) (4, 1) (3, 4, 2)
a:[[[7 1]]
[[8 5]]
[[4 8]]]
b:[[2]
[0]
[7]
[0]]
c:[[[ 9 3]
[ 7 1]
[14 8]
[ 7 1]]
[[10 7]
[ 8 5]
[15 12]
[ 8 5]]
[[ 6 10]
[ 4 8]
[11 15]
[ 4 8]]]
以上就是numpy的四则运算、矩阵运算以及广播机制的作用机制了。
5. 总结
- 数组的四则运算
∑ i , j M , N ( a i j + ∣ − ∣ ∗ ∣ / b i j ) \sum_{i, j}^{M,N}(a_{ij} + | - | * | / b_{ij}) i,j∑M,N(aij+∣−∣∗∣/bij)
- 矩阵相乘
C i , j = a i , 0 ∗ b 0 , j + a i , 1 ∗ b 1 , j + . . . + a i , n ∗ b n , j = ∑ k = 0 n a i k b k j C_{i,j} = a_{i,0}*b_{0,j}+a_{i,1}*b_{1,j}+...+a_{i,n}*b_{n,j} = \sum_{k=0}^{n}a_{ik}b_{kj} Ci,j=ai,0∗b0,j+ai,1∗b1,j+...+ai,n∗bn,j=k=0∑naikbkj
-
广播机制的三种场景
-
维度不相等两个数组的右侧轴元素个数相符
-
维度相等且其中之一的轴的元素个数为1且其它轴的元素个数相等
-
维度不相等两个数组的右侧元素个数不相符且一侧元素个数为1则按照两侧元素个数多的为标准进行广播
则满足广播机制。
-
写在末尾
- 博客简介专注AIoT领域追逐未来时代的脉搏记录路途中的技术成长
- 专栏简介从0到1掌握数据科学常用库Numpy、Matploblib、Pandas。
- 面向人群AI初级学习者
- 专栏计划接下来会逐步发布跨入人工智能的系列博文敬请期待
- Python零基础快速入门系列
- Python数据科学系列
- 人工智能开发环境搭建系列
- 机器学习系列
- 物体检测快速入门系列
- 自动驾驶物体检测系列
- …


