1. 协方差

概念

方差和标准差的原理和实例演示请参考

方差

方差Variance是度量一组数据的分散程度。方差是各个样本与样本均值的差的平方和的均值

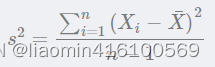
标准差

标准差是数值分散的测量。
标准差的符号是 σ 希腊语字母 西格马英语 sigma
公式很简单方差的平方根。

协方差

通俗理解

可以通俗的理解为两个变量在变化过程中是同方向变化还是反方向变化同向或反向程度如何
你变大同时我也变大说明两个变量是同向变化的这时协方差就是正的。
你变大同时我变小说明两个变量是反向变化的这时协方差就是负的。
从数值来看协方差的数值越大两个变量同向程度也就越大。反之亦然。
通俗易懂的理解看知乎文章 或者 gitlab转载

协方差矩阵

协方差Covariance在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况即当两个变量是相同的情况。 这个解释摘自维基百科看起来很是抽象不好理解。其实简单来讲协方差就是衡量两个变量相关性的变量。当协方差为正时两个变量呈正相关关系同增同减当协方差为负时两个变量呈负相关关系一增一减。而协方差矩阵只是将所有变量的协方差关系用矩阵的形式表现出来而已。通过矩阵这一工具可以更方便地进行数学运算。
数学定义
回想概率统计里面关于方差的数学定义

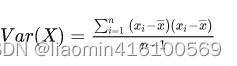
协方差的数学定义异曲同工

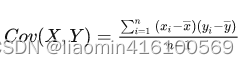
这里的 x和y表示两个变量空间。用机器学习的话讲就是样本有 x和 y两种特征
而 X 就是包含所有样本的 x特征的集合
Y就是包含所有样本的 y特征的集合。
用一个例子来解释会更加形象。

用一个矩阵表示为

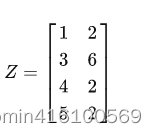
现在我们用两个变量空间X Y 来表示这两个特征

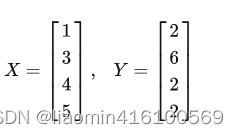
由于协方差反应的是两个变量之间的相关性因此协方差矩阵表示的是所有变量之间两两相关的关系具体来讲一个包含两个特征的矩阵其协方差矩阵应该有 2*2 大小

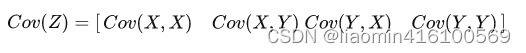
接下来就来逐一计算 Cov(Z)的值。 首先我们需要先计算出 XY 两个特征空间的平均值
AVG(X)=3.25,AVG(Y)=3 。 然后根据协方差的数学定义计算协方差矩阵的每个元素

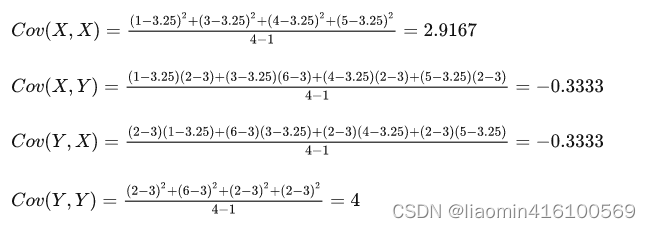
所以协方差矩阵

好了虽然这只是一个二维特征的例子但我们已经可以从中总结出协方差矩阵
的「计算套路」

python协方差原理

# 协方差主要是多个特征
pa=np.array([
     [1,2] ,
     [3,6] ,
     [4,2] ,
     [5,2] 
   ])
'''
 x应该是个二维矩阵表示
 [
     [1] ,
     [3] ,
     [4] ,
     [5] 
   ]
'''
x=np.array([pa[:,0]]).reshape((4,1))
'''
 y应该是个二维矩阵表示
 [
     [2] ,
     [6] ,
     [2] ,
     [2] 
   ]
'''
y=np.array([pa[:,1]]).reshape((4,1))
print("分别获取X和Y:",x,y)
x_mean=np.mean(x)
y_mean=np.mean(y)
print("x和y特征的均值",x_mean,y_mean)
'''
这里只是求第一个特征x第一列和第二个特征(第二列)的方差cov(x,y)
实际还有cov(x,x),cov(y,x),cov(y,y)
x-x_mean转置T就变成了
 [
     [1-xmean,3-xmean,4-xmean,5-xmean] 
 ]
y-ymean是
 [
     [2-ymean] ,
     [6-ymean] ,
     [2-ymean] ,
     [2-ymean] 
 ]
(x-x_mean).T.dot(y-y_mean)就变成了矩阵乘法了

1-xmean*2-ymean+3-xmean*6-ymean+4-xmean*2-ymean+5-xmean*2-ymean
然后除以n-1就是协方差了cov(x,y)
'''
print("cov(x,y)=",np.sum((x-x_mean).T.dot(y-y_mean))/(len(pa)-1))

#数学表示横表示列竖表示行默认行横表示特征
'''
[[1 3 4 5]
 [2 6 2 2]]
'''
print(pa.T)
print("conv",np.cov(pa.T))
# 使用rowvar=False表示列是变量是特征
print("conv",np.cov(pa,rowvar=False))

输出结果可查看github

2. PCA

概念

主成分分析(Principal Component Analysis):

• 一个非监督的机器学习算法
• 主要用于数据的降维
• 通过降维可以发现更便于人类理解的特征
• 其他应用可视化降噪

假设存在一根直线将所有的点都映射在该条指直线上这样的话点的整体分布和原来的点的分布就没有很大的差异点和点的距离比映射到x轴或者映射到y轴都要大区分度就更加明显与此同时所有的点都在一个轴上理解成一个维度虽然这个轴是斜着的。用这种方式将二维降到了一维度

公式推导

那么如何找到这个让样本间距最大的轴

如何定义样本间间距 使用方差(Variance)

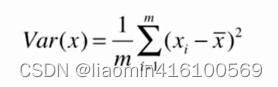
方差越大代表样本之间越稀疏方差越小代表样本之间越紧密。
移动坐标轴使得样本在每一个维度均值都为0

创建一个3x+4线性附近20个随机样本样例和结果https://github.com/lzeqian/machinelearn/blob/master/sklean_pca/demean.ipynb

import numpy as np;
import matplotlib.pyplot as plot
from commons.common import setXY
#生成一个 3x+4附近的点
np.random.seed(100);
# 获取randc个随机点
randc=20
x1=np.random.rand(randc);
x2=x1*3+4+np.random.rand(randc);
plot.plot(x1,x2,"o");

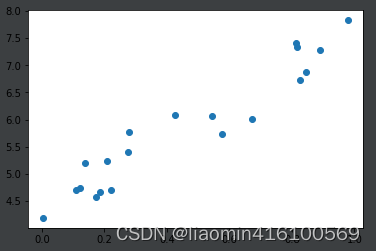
转换为矩阵表示

#使用矩阵数组表示,x1,x2  x1和x2是两个特征
'''
[   [x1,x2]
    [1,2],
    [3,4]
]
X=x1.reshape(-1,1); 等价于x1.reshape(len(x1),1)
[1,2]转换为
x1=[
  [1],
  [2]
]
x2=[
  [4],
  [5]
]
x1.hstack(x2)
[
  [1,4],
  [2,5]
]
'''
X=np.hstack((x1.reshape(len(x1),1),x2.reshape(len(x2),1)))
print(X)
[[0.54340494 6.06191901]
 [0.27836939 5.77513797]
 [0.42451759 6.09120215]
 [0.84477613 6.87044035]
 [0.00471886 4.18956702]
 [0.12156912 4.73753941]
 [0.67074908 6.01793576]
 [0.82585276 6.72998462]
 [0.13670659 5.20578228]
 [0.57509333 5.74053496]
 [0.89132195 7.27280924]
 [0.20920212 5.23141091]
 [0.18532822 4.66113234]
 [0.10837689 4.70707412]
 [0.21969749 4.69556853]
 [0.97862378 7.82628292]
 [0.81168315 7.4159703 ]
 [0.17194101 4.57576503]
 [0.81622475 7.33922019]
 [0.27407375 5.39912274]]

demean均值归0处理

np.set_printoptions(suppress=True) #不使用科学计数法
setXY()
def demean(X):
    return X-np.mean(X,axis=0) #取对应列的均值
#均值归零的算法是x1-xmeanx2-x2mean
X_demean=demean(X)
plot.plot(X_demean[:,0],X_demean[:,1],"o");

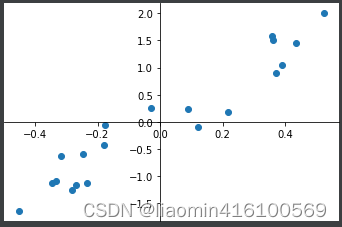
demean之后的方差最大其实就是求映射后每个点到(0,0)的距离最大再求和假设降维后轴的方向是w=(w1, w2)

Xi是映射前的向量Xi(project)是映射后的向量这里注意w向量是单位向量 |w|=1

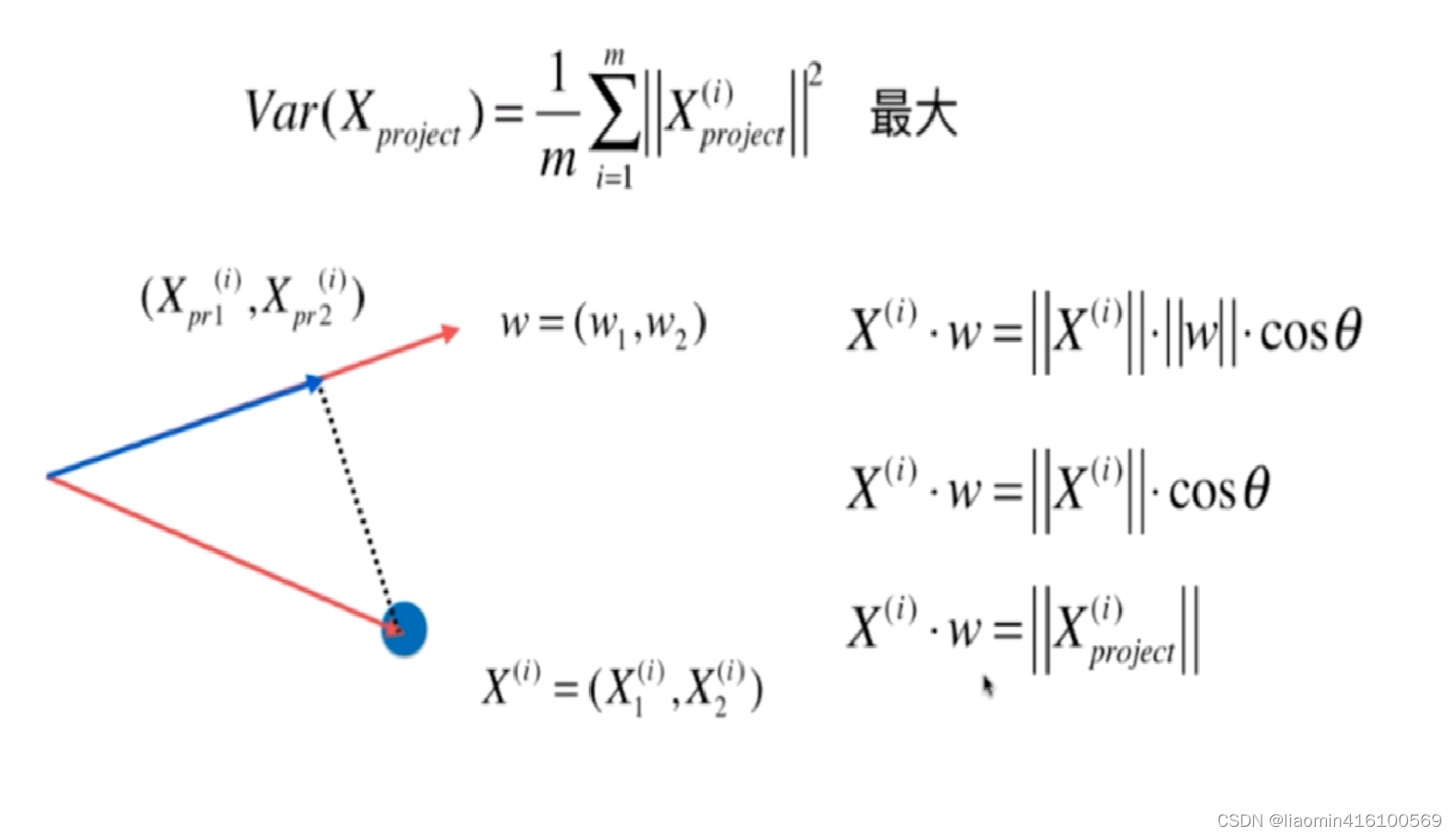
以上是推导公式
目标函数是

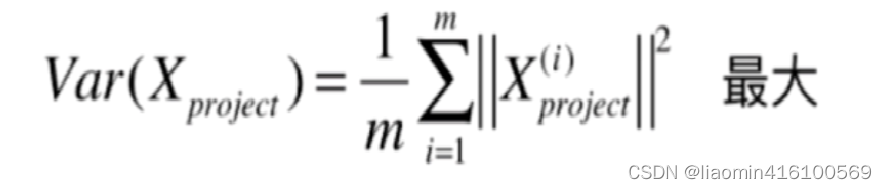
通过公司可知

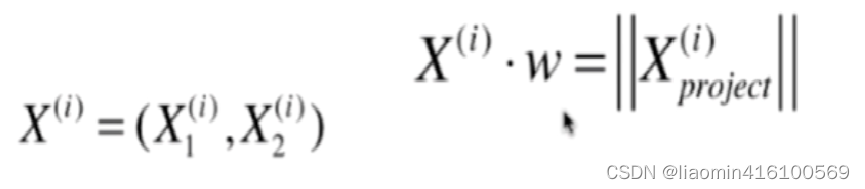
注意i是样本索引下标12是特征数x1是特征1x2是特征2 xj是特征j每个特征xj对应一个维度wj

目标函数即

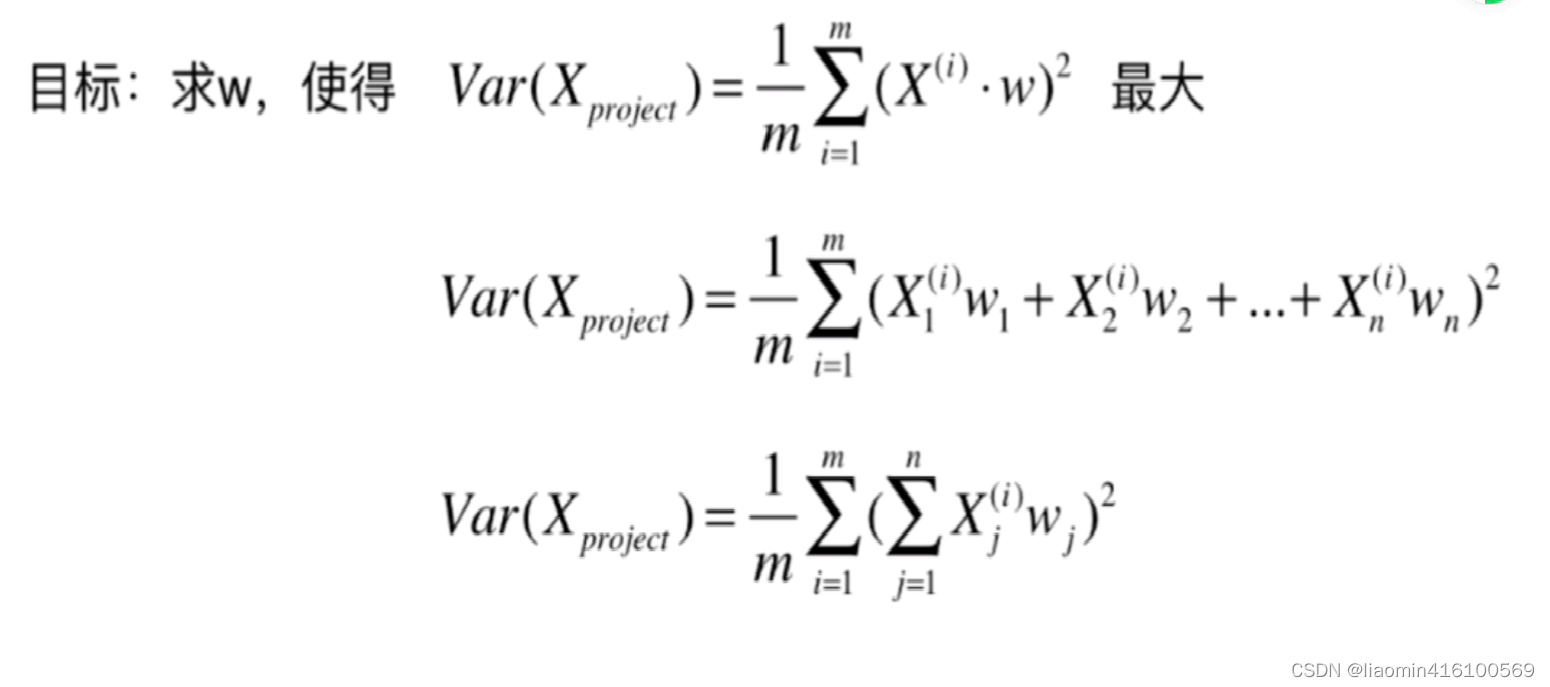
对目标函数求梯度

转化为

由于最终转换的结果是一个1行m列的矩阵而我们想要得到一个n行1列的矩阵所以还要进行一次转置

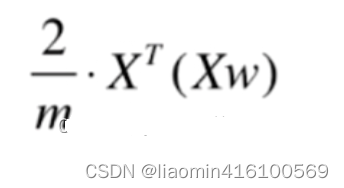
编程实现第一主成分

产生一个 3x+4附近的点

import numpy as np;
import matplotlib.pyplot as plot
from commons.common import setXY
#生成一个 3x+4附近的点
#np.random.seed(100);
# 获取randc个随机点
randc=100
# 0-1的数*多少倍注意太小的样本点abs(f(w=w, X=X) - f(w=last_w, X=X)) 的值增量过小可能导致循环次数后还没有到<epsilon导致拟合不准确
# 如果是1建议循环次数加大100000
# 如果是100 可以设置为100
blow=100
x1=np.random.rand(randc)*blow;
x2=x1*3+4+np.random.rand(randc)*blow;
plot.plot(x1,x2,"o");
X=np.hstack((x1.reshape(len(x1),1),x2.reshape(len(x2),1)))
np.set_printoptions(suppress=True) #不使用科学计数法

定义目标函数

# 这是目标函数 np.sumX*W**2)/M
# 注意目标函数是传入X是已知的数据样本w是个2个特征向量 f(w1,w2)是个三位空间

def f(X,w):
    return np.sum((X.dot(w))**2)/len(X)

获取w在各个特征的导数

# 获取各个维度的导数    
def df_w(X,w):
    return X.T.dot(X.dot(w))*2/len(X)

也可以用这个通用的方法求导数

'''
通用计算某个点的斜率的方法
为了验证我们的这个是正确的使用这个df_debug这个函数
和线性下降法一样使两个点之间连成的直线不断的靠近应得的直线
使其斜率相当注意的是这里的epsilon取值比较小是因为在PCA的梯度上升法中
w是一个方向向量其模为1所以w的每一个维度其实都很小那么为了适应相应的epsilon也要小一些
'''
def df_debug(w,X,epsilon=0.0001):
      res = np.empty(len(w))
      for i in range(len(w)):
          w_1 = w.copy()
          w_1[i] += epsilon
          w_2 = w.copy()
          w_2[i] -= epsilon
          res[i] = (f(w=w_1,X=X) - f(w=w_2,X=X)) / (2*epsilon)

将w向量转换为单位向量

# 将任意向量转换为单位向量 np.linalg.norm(w)是 x**2+x1**2开根号
# (3,4)/5=(3/5,4/5)就是单位向量模是1
def direction(w):
    return w / np.linalg.norm(w)

梯度上升测试

wapp=np.array([])
def gradient_ascent(df, X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
    w = direction(initial_w)
    i_iter = 1
    global wapp
    wapp=np.append(wapp,w).reshape((1,len(w)))
    while i_iter < n_iters:
        gradient = df(w=w, X=X)
        last_w = w
        # gradient是对每个维度求偏导得到的列表如果偏导数为负则w的这个维度加上一个负值降维后的方差趋于变大
        # 如果偏导数为正则w的这个维度加上一个正值降维后的方差趋于变大因此w加上导数值降维后的方差趋于变大
        # 在eta合适的情况下随着循环进行导数值逐渐趋近0eta是常数降维后的方差的变化量会越来越小
        w = w + eta * gradient
        w = direction(w)  # 注意1每次求一个单位向量
        wapp=np.vstack((wapp,np.array([w])))
        # abs求绝对值
        if (abs(f(w=w, X=X) - f(w=last_w, X=X)) < epsilon):
            print("精度",abs(f(w=w, X=X) - f(w=last_w, X=X)),epsilon)
            print("梯度",gradient)
            
            break
        i_iter += 1
    return w


initial_w = np.random.random(X.shape[1])  # 注意2不能用0向量开始
eta = 0.0001
# print(gradient_ascent(df_debug, X=X_demean, initial_w=initial_w, eta=eta))
w=(gradient_ascent(df_w, X=X_demean, initial_w=initial_w, eta=eta, n_iters=100))
setXY()
plot.plot(X_demean[:,0],X_demean[:,1],"o");
print(w)
# 单位向量乘同一个方向是相同的
plot.plot([0,w[0]*(blow)],[0,w[1]*blow])
#plot.plot(X_demean[:,0],w[1]/w[0]*X_demean[:,0])
#%%
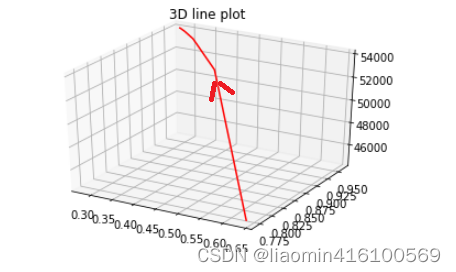
fig = plot.figure()
#创建梯度上升的过程
ax = plot.axes(projection='3d')
wappy=[f(w=w_t, X=X) for w_t in wapp]
ax.plot3D(wapp[:,0],wapp[:,1],wappy, 'red')
print("w1值",wapp[:,0])
print("w2值",wapp[:,1])
print("方差",wappy)

ax.set_title('3D line plot')
plot.show()

拟合的直线

梯度上升过程