机器学习笔记之深度玻尔兹曼机(二)深度玻尔兹曼机的预训练过程

引言

上一节介绍了玻尔兹曼机系列的相关模型本节将介绍深度玻尔兹曼机的预训练过程。

深度信念网络预训练过程的问题

在玻尔兹曼机系列整体介绍中提到过无论是深度信念网络还是深度玻尔兹曼机它们建模的核心思想是叠加$\text{RBM}$结构。以一个三层结构$v,h^{(1)},h^{(2)}$为例观察未叠加时的状态表示如下

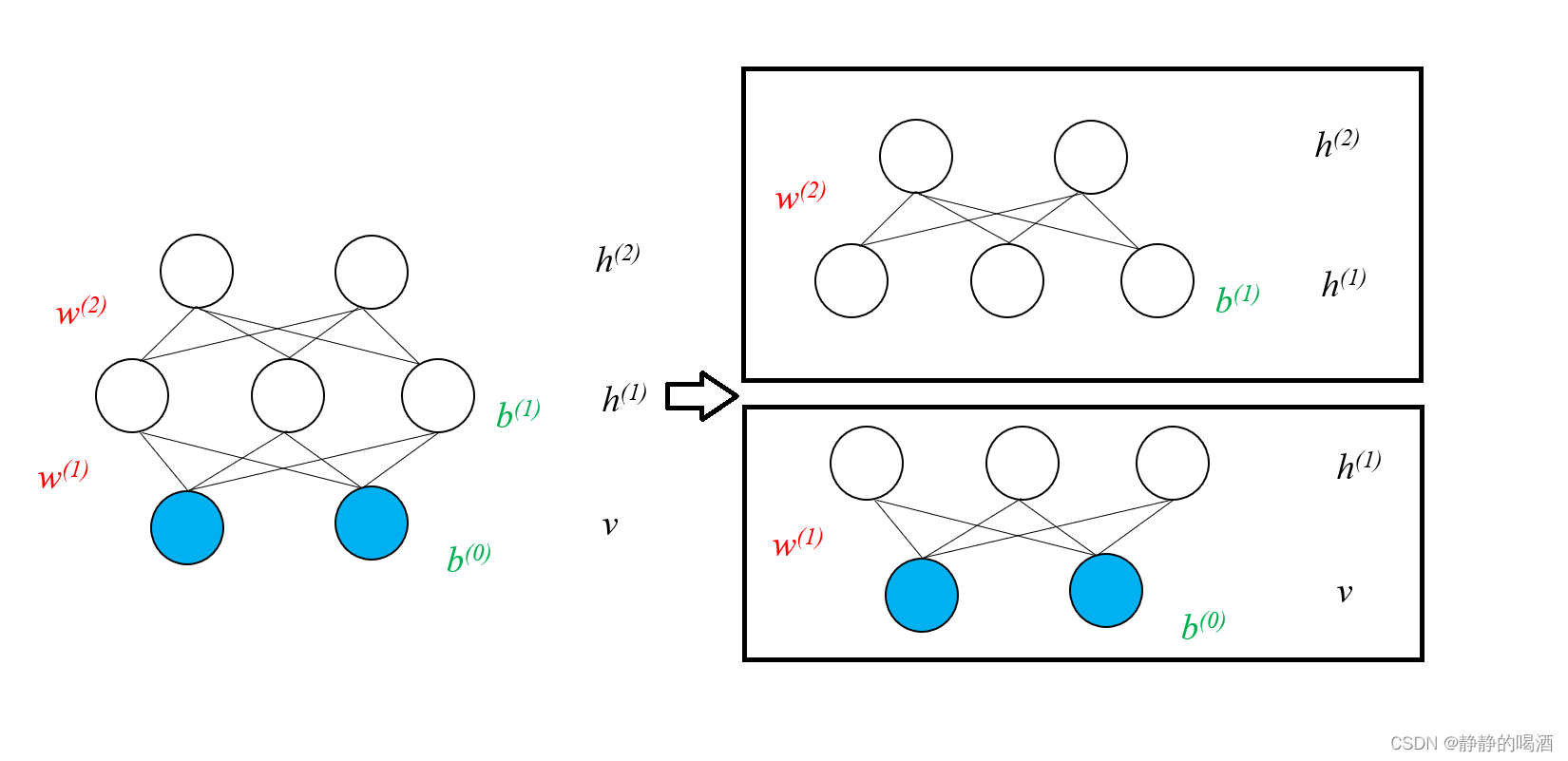
实际上深度信念网络与深度玻尔兹曼机的学习过程是相同的。以深度信念网络为例上图的学习过程可分为两个部分
在受限玻尔兹曼机——对数似然梯度中介绍过可以通过'对比散度'的方式求解模型参数的对数似然梯度再通过梯度上升法对模型参数进行近似求解。在这里求解模型参数并不是重点只需要知道模型参数是可以求解的即可。

• 第一层学习过程第一层本质上就是一个受限玻尔兹曼机关于观测变量的似然函数$\mathcal{P}(v)$可表示如下:
  $$\mathcal{P}(v)=\sum _{h^{(1)}}\mathcal{P}(v,h^{(1)})=\sum _{h^{(1)}}\mathcal{P}(h^{(1)})\cdot \mathcal{P}(v\mid h^{(1)})$$
  关于两个概率分布$\mathcal{P}(h^{(1)}),\mathcal{P}(v\mid h^{(1)})$在玻尔兹曼机系列整体介绍中提到过它们均可以通过模型参数进行表示

  • $\mathcal{P}(h^{(1)})$可表示为如下形式
    关于‘联合概率分布’$\mathcal{P}(v,h^{(1)})$详见受限玻尔兹曼机——模型表示
    这里为方便观看起见暂时将各随机变量与自身关联关系对应的偏置项$b,c$忽略掉。
    $$\begin{array}{rl}\mathcal{P}(h^{(1)})& =\sum _v\mathcal{P}(v,h^{(1)})\\ & =\sum _v\frac{1}{\mathcal{Z}}\exp [v^T{\mathcal{W}}^{(1)}\cdot h^{(1)}]\end{array}$$
  • $\mathcal{P}(v\mid h^{(1)})$根据受限玻尔兹曼机——后验概率可表示为如下形式
    $$\begin{array}{rl}\mathcal{P}(v\mid h^{(1)})& =\prod _{k=1}^{|\mathcal{D}|}\mathcal{P}(v_k\mid h^{(1)})\\ \mathcal{P}(v_k\mid h^{(1)})& =\text{Sigmoid}\left(\sum _{j=1}^{|\mathcal{P}|}{w}_{k}j\cdot h_j+b_k\right)w_{kj}\in {\mathcal{W}}^{(1)}\end{array}$$

  这里仅需要知道$\mathcal{P}(h^{(1)}),\mathcal{P}(v\mid h^{(1)})$可以使用${\mathcal{W}}^{(1)}$进行表示即可这里使用符号$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)}),\mathcal{P}(v\mid h^{(1)};{\mathcal{W}}^{(1)})$进行表示
  第一层学习过程的重点在于边缘概率分布$\mathcal{P}(h^{(1)})$仅和模型参数${\mathcal{W}}^{(1)}$之间存在关联关系。
  $$\mathcal{P}(v;{\mathcal{W}}^{(1)})=\sum _{h^{(1)}}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})\cdot \mathcal{P}(v\mid h^{(1)};{\mathcal{W}}^{(1)})$$

• 第二层学习过程第二层同样也是一个受限玻尔兹曼机如果是处理方式和第一层是完全相同的。但第二层需要的样本是关于$h^{(1)}$随机变量结点相关的样本而我们只有观测变量$v$的样本$\mathcal{V}$。
  因此必然需要关于$h^{(1)}$的样本。因而需要从第一层的后验$\mathcal{P}(h^{(1)}\mid v)$中采集样本。关于后验$\mathcal{P}(h^{(1)}\mid v)$表示如下
  受限玻尔兹曼机各隐变量之间相互条件独立这是受限玻尔兹曼机自身的结构性质。
  $$\mathcal{P}(h^{(1)}\mid v)=\prod _{l=1}^{|{\mathcal{P}}^{(1)}|}\mathcal{P}(h_l\mid v)$$
  关于隐变量集合$h^{(1)}$中的某一个隐变量$h_l$的后验分布表示如下。通过对该概率分布进行采样可以得到关于$\mathcal{P}(h_l\mid v)$的样本信息。
  $$\mathcal{P}(h_l\mid v)=\{\begin{array}{l}\text{Sigmoid}\left({\sum }_{i=1}^n{w}_{li}\cdot v_i+c_l\right)h_l=1\\ 1-\text{Sigmoid}\left({\sum }_{i=1}^n{w}_{li}\cdot v_i+c_l\right)h_l=0\end{array}$$
  至此有了关于$h^{(1)}$的样本之后可以和第一层学习过程一样对第二层的隐变量$h^{(2)}$进行表示
  和第一层的过程相同这里不再赘述。
  $$\begin{array}{rl}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})& =\sum _{h^{(2)}}\mathcal{P}(h^{(1)},h^{(2)};{\mathcal{W}}^{(2)})\\ & =\sum _{h^{(2)}}\mathcal{P}(h^{(2)};{\mathcal{W}}^{(2)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\end{array}$$

在深度信念网络中它将上述两层受限玻尔兹曼机堆叠的过程中它仅仅是将$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$通过新构建一层模型从而构成新的受限玻尔兹曼机进行学习。从公式的角度观察它将$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$替换了$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$
$$\begin{array}{rl}\text{DBN : }\mathcal{P}(v;{\mathcal{W}}^{(1)})& =\sum _{h^{(1)}}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})\cdot \mathcal{P}(v\mid h^{(1)};{\mathcal{W}}^{(1)})\\ & =\sum _{h^{(1)}}\left[\sum _{h^{(2)}}\mathcal{P}(h^{(2)};{\mathcal{W}}^{(2)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\right]\cdot \mathcal{P}(v\mid h^{(1)};{\mathcal{W}}^{(1)})\end{array}$$
但在3层网络中也就是第一层第二层合并的情况下关于隐变量集合$h^{(1)}$的 真实后验 是什么在混合后的3层网络中边缘概率分布$\mathcal{P}(h^{(1)})$表示如下
$$\mathcal{P}(h^{(1)})=\sum _{h^{(2)},v}\mathcal{P}(v,h^{(1)},h^{(2)})$$
虽然此时没有办法写出该网络的联合概率分布表示但不可否认的是$\mathcal{P}(v,h^{(1)},h^{(2)})$必然和参数${\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)}$均有关联
$$\mathcal{P}(h^{(1)})\Rightarrow \mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})$$
也就是说深度信念网络仅用包含${\mathcal{W}}^{(2)}$的表示近似了真实表示
$$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})\approx \mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})$$
此时在两个受限玻尔兹曼机叠加之后无论是单个受限玻尔兹曼机的$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$还是深度信念网络的$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$它们的表示 都是不准确的。能否存在一个想法让$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$和$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$联合在一起去近似$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})$呢

深度玻尔兹曼机的预训练过程(2023/1/24)

针对上述问题存在这样一个想法既然想要联合近似可以将$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$和$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$对应取算数平均值
$$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})\approx \frac{1}{2}\left[\mathcal{P}(h^{(1)}\mid {\mathcal{W}}^{(1)})+\mathcal{P}(h^{(1)}\mid {\mathcal{W}}^{(2)})\right]$$
这种说法并非绝对算数平均值仅是一种具体操作而背后的思想是相比于深度信念网络$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})\approx \mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)},{\mathcal{W}}^{(2)})$能否在两个受限玻尔兹曼机结合在一起后关于边缘概率分布$\mathcal{P}(h^{(1)})$的描述让${\mathcal{W}}^{(1)}$也参与进来而不是仅使用${\mathcal{W}}^{(2)}$进行描述。

虽然受限玻尔兹曼机对模型结构存在严苛要求但这些要求主要影响的是观测变量、隐变量之间的关系对应的是条件概率$\mathcal{P}(h^{(1)}\mid v^{(1)})$或者$\mathcal{P}(v^{(1)}\mid h^{(1)})$。这意味着条件概率能够被准确表示。

但边缘概率分布$\mathcal{P}(h^{(1)})$并不能被精确表示而只能被近似表示。观察$\mathcal{P}(h^{(1)})$的展开式可以通过蒙特卡洛方法进行近似

• 关于${\sum }_{v^{(1)}}$内包含$N$个也就是样本数量个连加项可看作计算代价为∞而针对这种期望形式的表达使用蒙特卡洛方法近似是完全可以实现的。
• 关于$\frac{1}{N}{\sum }_{v^{(i)}\in \mathcal{V}}\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})$这种求解方式也被称作$\text{appregated posterior Distribution}$聚合后验分布后验自然是指$\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})$,而聚合是指本想从‘真实分布’${\mathcal{P}}_{data}/\mathcal{P}(v^{(1)})$中进行采样但实际上真实分布是无法得到的而只有$N$个真实样本通过$N$个真实样本的‘经验分布’作为采样分布来近似${\mathcal{P}}_{data}$.

$$\begin{array}{rl}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})& =\sum _{v^{(1)}}\mathcal{P}(v^{(1)},h^{(1)};{\mathcal{W}}^{(1)})\\ & =\sum _{v^{(1)}}\mathcal{P}(v^{(1)})\cdot \mathcal{P}(h^{(1)}\mid v^{(1)};{\mathcal{W}}^{(1)})\\ & ={\mathbb{E}}_{\mathcal{P}(v^{(1)})}\left[\mathcal{P}(h^{(1)}\mid v^{(1)};{\mathcal{W}}^{(1)})\right]\\ & \approx \frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})\end{array}$$
同理关于参数${\mathcal{W}}^{(2)}$表示的边缘概率分布$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$使用蒙特卡洛方法表示为
其中$\mathcal{H}$表示从$\mathcal{P}(h^{(2)})$中采样所产生的样本集合。不同于$\mathcal{P}(v^{(1)})$中的具体样本准确的说它是经过两次迭代采样得到的样本
$$\begin{array}{r}\mathcal{P}(h^{(1)})\Leftarrow {\left\{h^{(1),i}\right\}}_{i=1}^N\sim \mathcal{P}(h^{(1)}\mid v^{(1)};{\mathcal{W}}^{(1)})\end{array}$$

• 上述是第一层产生的样本。很明显它是从后验分布$\mathcal{P}(h^{(1)}\mid v^{(1)};{\mathcal{W}}^{(1)})$中采集出来的但真正想要的是$\mathcal{P}(h^{(1)})$自身的分布。而$\mathcal{P}(h^{(1)})$分布和$\mathcal{P}(v^{(1)})$一样没有办法求出准确解。因此将采样得到的 { h ( 1 ) , i } i = 1 N \{h^{(1),i}\}_{i=1}^N {h(1),i}i=1N​所形成的经验分布近似为 $\mathcal{P}(h^{(1)})$.
  $$\mathcal{P}(h^{(2)})\Leftarrow {\left\{h^{(2),j}\right\}}_{j=1}^N=\mathcal{H}\sim \mathcal{P}(h^{(2)}\mid h^{(1)};{\mathcal{W}}^{(2)})$$
• 此时已经得到了$h^{(1)}$的样本上述描述的是以相同方法产生的第二层样本。

$$\begin{array}{rl}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})& =\sum _{h^{(2)}}\mathcal{P}(h^{(1)},h^{(2)};{\mathcal{W}}^{(2)})\\ & =\sum _{h^{(2)}}\mathcal{P}(h^{(2)})\cdot \mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\\ & ={\mathbb{E}}_{\mathcal{P}(h^{(2)})}\left[\mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\right]\\ & \approx \frac{1}{N}\sum _{h^{(2)}\in \mathcal{H}}\mathcal{P}(h^{(1)}\mid h^{(2)};{\mathcal{W}}^{(2)})\end{array}$$

此时两个网络层关于$\mathcal{P}(h^{(1)})$的聚合后验分布表示结束后在两网络层融合过程中关于$\mathcal{P}(h^{(1)})$的描述以算术平均值为例可能得到如下结果
这仅仅描述的是通过不同参数得到的聚合后验分布的融合过程。
$$\begin{array}{rl}\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)};{\mathcal{W}}^{(2)})& \approx \frac{1}{2}\left[\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})+\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})\right]\\ & =\frac{1}{2N}\left[\sum _{v^{(i)}\in \mathcal{V}}\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})+\sum _{h^{(2)}\in \mathcal{H}}\mathcal{P}(h^{(2)}\mid h^{(1)};{\mathcal{W}}^{(2)})\right]\end{array}$$
这种模型融合的方式是否存在问题这种相加的方式会存在$\text{Double Counting}$现象。在上面的描述中样本集合$\mathcal{V}$和$h^{(2)}$对应的样本集合$\mathcal{H}$之间并不是相互独立的而是通过$\text{bottom-up}$方法逐级生成出来的
$$\begin{array}{rl}\mathcal{V}& \Rightarrow \underset{近似计算\mathcal{P}(h^{(1)})}{\underbrace{\frac{1}{N}\sum _{v^{(i)}\in \mathcal{V}}\mathcal{P}(h^{(1)}\mid v^{(i)};{\mathcal{W}}^{(1)})\approx \mathcal{P}(h^{(1)})}}\\ & \Rightarrow \underset{从\mathcal{P}(h^{(1)})中抽取样本组成关于h^{(1)}的隐变量样本集合\hat{\mathcal{H}}}{\underbrace{\hat{\mathcal{H}}={\left\{h^{(1),i}\right\}}_{i=1}^N\sim \mathcal{P}(h^{(1)})}}\\ & \Rightarrow \underset{近似计算\mathcal{P}(h^{(2)})}{\underbrace{\frac{1}{N}\sum _{h^{(1)\in \hat{\mathcal{H}}}}\mathcal{P}(h^{(2)}\mid h^{(1)};{\mathcal{W}}^{(2)})\approx \mathcal{P}(h^{(2)})}}\\ & \Rightarrow \underset{从\mathcal{P}(h^{(2)})中抽取样本组成关于h^{(2)}的因变量样本集合\mathcal{H}}{\underbrace{\mathcal{H}={\left\{h^{(2),j}\right\}}_{j=1}^N\sim \mathcal{P}(h^{(2)})}}\end{array}$$
很明显可以观察到

• 计算$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(2)})$时需要使用隐变量样本集合$\mathcal{H}$隐变量样本集合$\mathcal{H}$生成过程中就已经用过样本集合$\mathcal{V}$一次
• 计算$\mathcal{P}(h^{(1)};{\mathcal{W}}^{(1)})$时需要使用样本集合$\mathcal{V}$此时又用了一次

这意味着样本集合$\mathcal{V}$被重复使用了。这种操作会产生什么影响会使得该模型表达的分布过于尖锐。何为尖锐即样本分布极差很大。为何会产生这种情况因为假设通过采样得到了两个完全相同的样本即便他们在样本空间中重合那也是两个样本而样本集合在描述概率分布过程中使用的是 经验分布在重复使用样本集合$\mathcal{V}$时整个经验分布会产生严重的数值上的分裂

• 数据密集的部分可能会影响较小(概率密度函数下降的程度较小)或者说经验分布分子、分母之间比率相差不大
• 而数据不密集的部分会有较大影响虽然分子数值上升但远没有分母增加的多这使得概率密度函数相比之前更小了。
• 这种分布可能没有缓冲区间对应模型产生的生成样本也会存在特征上的较大缺陷。

相关参考
深度玻尔兹曼机2-预训练1-介绍