机器学习之求解无约束最优化问题方法(手推公式版)

前言

  本篇博文主要介绍了机器学习里面的常见的求解无约束最优化问题的方法包括梯度下降法、牛顿法和拟牛顿法并给出了相关的推导过程及代码实现。

  本篇博文内容主要来自李航老师的《统计学习方法》附录A和B。

1. 基础知识

1.1 方向导数

  在许多问题中我们不仅要知道函数再坐标轴上的变化率即偏导数而且还要设法求得函数在某点沿着其他特定方向上的变化率这就是方向导数。
  方向导数的计算公式如下设三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,z_0)$处可微分则$u=u(x,y,z)$在点$P_0$处沿任一方向 $\mathbf{l}$ 的方向导数都存在则

1.2 梯度

  在一个数量场中函数在给定点处沿不同的方向其方向导数一般都是不相同的现在我们关心的是沿哪一个方向其方向导数最大最大值是多少函数在点$P$沿哪一个方向增加的速度最快由此引入了梯度这一概念。
  设三元函数$u=u(x,y,z)$在点$P_0(x_0,y_0,z_0)$处具有一阶偏导数则定义$$\mathbf{grad}u{|}_{P_0}=(u_x^{\prime }(P_0),u_y^{\prime }(P_0),u_z^{\prime }(P_0))$$  为函数$u=u(x,y,z)$在点$P_0(x_0,y_0,z_0)$处的梯度。

1.3 方向导数与梯度的关系

  由方向导数的计算公式和梯度的定义可以得到

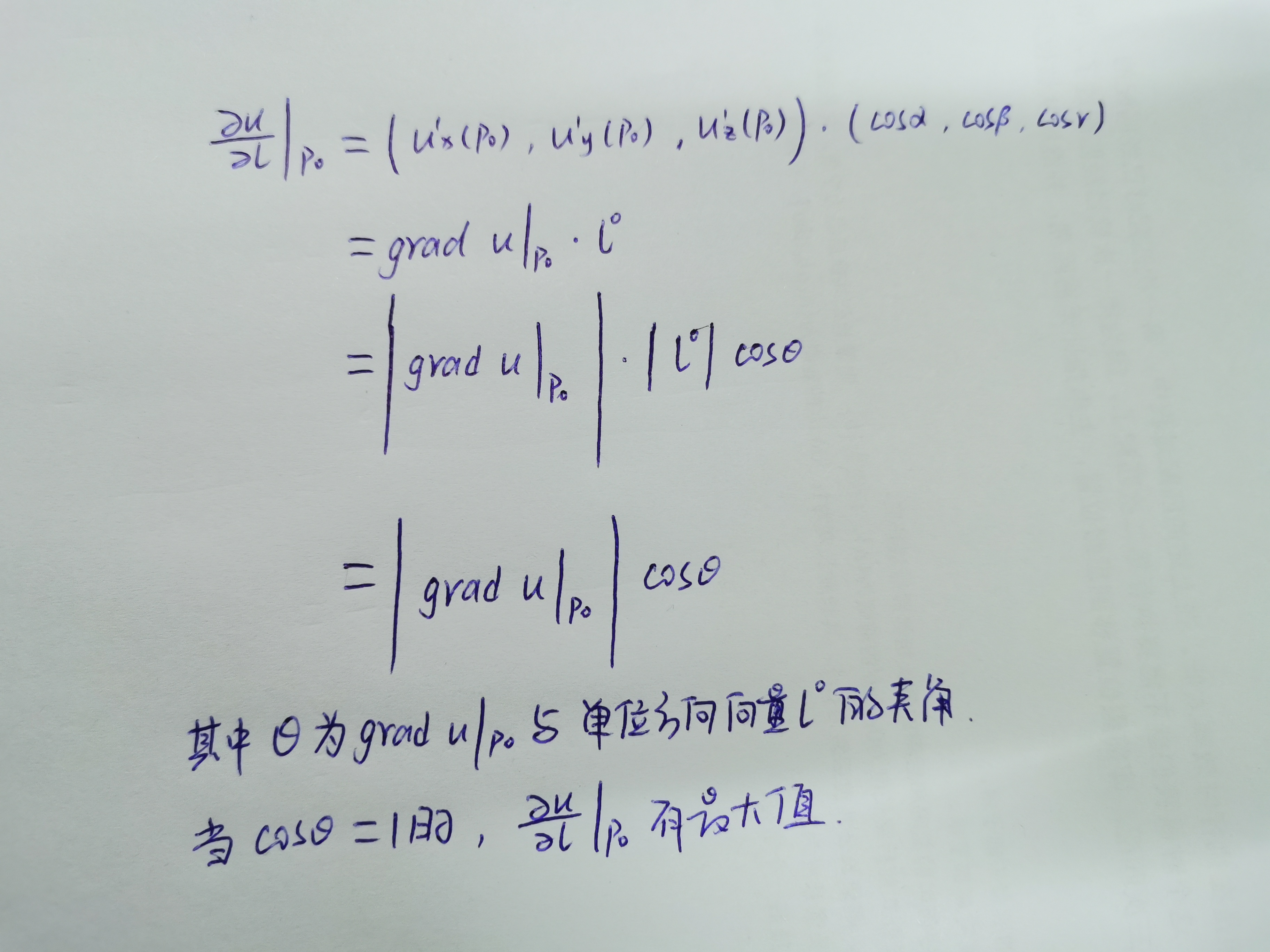
  由上可以得到如下结论函数在某点的梯度是一个向量它的方向与取得最大方向导数的方向一致而它的模为方向导数的最大值再通俗点说梯度的方向就是变化率最快的方向也就是函数值增加最快的方向。

1.4 泰勒展开公式

  设$f(x)$在点$x_0$的某个邻域内n+1阶导数存在则对该邻域内的任意点有$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{1}{2}{f}^{\prime \prime }(x_0)(x-x_0{)}^2+\cdots +\frac{1}{n!}{f}^{(n)}(x_0)(x-x_0{)}^n+\frac{1}{(n+1)!}{f}^{(n+1)}(\xi )(x-x_0{)}^{(n+1)}$$  其中$\xi$介于$x$和$x_0$之间。
  上述公式是带拉格朗日余项的n阶泰勒公式当$x_0=0$时上述泰勒公式又称为麦克劳林公式。

1.5 Jacobian矩阵与Hessian矩阵

  简单来说由一阶偏导数组成的矩阵叫做Jacobian矩阵(雅可比矩阵)由二阶偏导数组成的矩阵叫做Hessian矩阵(黑塞矩阵)。
  称矩阵$$J=\left[\begin{array}{cccc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& \dots & \frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& \dots & \frac{\partial f_2}{\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_n}{\partial x_1}& \frac{\partial f_n}{\partial x_2}& \dots & \frac{\partial f_n}{\partial x_n}\end{array}\right]$$为雅可比矩阵(Jacobian Matrix)也可记作$$\nabla f$$
  若$n$元函数$f(x)$在点$x$处对于自变量的各分量的二阶偏导数连续则称矩阵$$H(x)=\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial {x_1}^2}& \frac{{\partial }^{2}f}{\partial x_1{x}_2}& \dots & \frac{{\partial }^{2}f}{\partial x_1{x}_n}\\ \frac{{\partial }^{2}f}{\partial x_2{x}_1}& \frac{{\partial }^{2}f}{\partial {x_2}^2}& \dots & \frac{{\partial }^{2}f}{\partial x_2{x}_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_n{x}_1}& \frac{{\partial }^{2}f}{\partial x_n{x}_2}& \dots & \frac{{\partial }^{2}f}{\partial {x_n}^2}\end{array}\right]$$为$f(x)$在点$x$处的二阶导数或黑塞矩阵(Hessian Matrix)也可记作$${\nabla }^{2}f(x)$$  由此可以知道Hessian矩阵是一个对称矩阵。

1.6 正定矩阵

  $n$元二次型$f(x_1,x_2,\dots ,x_n)=x^{T}Ax$若对任意的$x=[x_1,x_2,\dots ,x_n{]}^T\ne 0$均有$x^{T}Ax>0$则成$f$为正定二次型二次型对应的矩阵$A$为正定矩阵。
  二次型正定的充分条件
  $n$元二次型$f=x^{T}Ax$正定 $⟺$ 对于任意$x\ne 0$有$x^{T}Ax>0$
              $⟺$ $f$的正惯性指数$p=n$
              $⟺$ 存在可逆矩阵$D$使$A=D^{T}D$
              $⟺$ $A$与$E$合同即存在矩阵$C$是$C^{T}AC=E$
              $⟺$ $A$的特征值${\lambda }_i>0(i=1,2,\dots ,n)$
              $⟺$ $A$的全部顺序主子式均大于0

  二次型正定的必要条件
  (1) $a_{ii}>0(i=0,1,\dots ,n)$
  (2) $|A|>0$

2. 梯度下降法

  梯度下降法$(gradientdescent,GD)$是求解无约束最优化问题的一种常用的方法具有简单的优点。梯度下降算法是迭代算法每一步需要求解目标函数的梯度向量。

  在《统计学习方法》中对梯度下降法的介绍如下
  设$f(x)$是$R^n$上具有一阶连续偏导数的函数。要求解的无约束最优化问题是$$\underset{x\in {\mathbf{R}}^n}{\min }f(x)$$  $x^{\ast }$表示目标函数$f(x)$的极小点。选取适当的初值$x_0$不断迭代更新$x$的值进行目标函数的极小化直到收敛。由于负梯度方向是使函数值下降最快的方向在迭代的每一步以负梯度方向更新$x$的值从而达到减少函数值的目的。
  由于$f(x)$具有一阶连续偏导数若第$k$次迭代值为$x_k$则可将$f(x)$在$x_k$附近进行一阶泰勒展开$$f(x)=f(x_k)+g_k(x-x_k)$$  其中$g_k=g(x_k)=\nabla f(x_k)$为$f(x)$在$x_k$的梯度。
  求出第$k+1$次迭代值$x_{k+1}$$$x_{k+1}\leftarrow x_k+{\lambda }_k{p}_k$$  其中$p_k$是搜索方向取负梯度方向$p_k=-\nabla f(x_k)=-g_k$${\lambda }_k$是步长(也就是学习率)由一维搜索确定即${\lambda }_k$使得$$f(x_k+{\lambda }_k{p}_k)=\underset{\lambda \ge 0}{\min }f(x_k+\lambda p_k)$$
  为方便计算这里将学习率固定

  当目标函数是凸函数时梯度下降法的解是全局最优解。一般情况下其解不保证是全局最优解。梯度下降法的收敛速度也未必是很快的。

3. 牛顿法

  相比梯度下降算法牛顿法使用的是二阶泰勒展开式。
  设$f(x)$具有二阶连续偏导数若第$k$次迭代值为$x_k$则可将$f(x)$在$x_k$附近进行二阶泰勒展开$$f(x)=f(x_k)+g_k(x-x_k)+\frac{1}{2}H(x_k)(x-x_k{)}^2$$  其中$g_k=g(x_k)=\nabla f(x_k)$为$f(x)$的梯度向量在$x_k$处的值$H(x_k)={\nabla }^{2}f(x_k)$为$f(x)$的黑塞矩阵$$H(x)=\left[\frac{{\partial }^{2}f}{\partial x_i\partial x_j}\right]$$在$x_k$处的值。
  函数$f(x)$有极值的必要条件是在极值点处一阶导数为0即梯度向量为0。特别是当$H(x_k)$是正定矩阵时函数$f(x)$的极值为极小值。

  (1) 类比一元函数判别极值的第二充分条件即$f(x)$在$x=x_0$处二阶可导且$f^{\prime }(x_0)=0$$f^{\prime \prime }(x_0)\ne 0$若$f^{\prime \prime }(x_0)>0$则$f(x)$在$x_0$处取极小值。
  (2) 类比二元函数取极值的充分条件若$H=\left[\begin{array}{cc}A& B\\ B& C\end{array}\right]$为正定矩阵根据正定矩阵的全部顺序主子式均大于0可知$A>0$$\Delta =AC-B^2>0$所以$f$有极小值。

  牛顿法利用极小点的必要条件$$\nabla f(x)=0$$  根据这一条件对$f(x)$的二阶泰勒展开式求导可得$$\nabla f(x)=g_k+H(x_k)(x-x_k)$$
  假设在$x_{k+1}$处也满足$\nabla f(x_{k+1})=0$则可以得到$$\nabla f(x_{k+1})=g_k+H(x_k)(x_{k+1}-x_k)$$  假进一步可以得到$$x_{k+1}=x_k-H_k^{-1}{g}_k$$  具体算法如下

  可见相比梯度下降法牛顿法的步长是自动计算出来的且收敛速度较快。

4. 拟牛顿法

  在牛顿法的迭代中需要计算黑塞矩阵的逆矩阵$H^{-1}$这一计算比较复杂考虑用一个$n$阶矩阵$G_k=G(x_k)$来近似代替$H_k^{-1}=H^{-1}(x_k)$这就是拟牛顿法的基本想法。

5. 代码实现

  代码实现如下

# -*- coding:utf-8 -*-
# Author:   liyanpeng
# Email:    youran.xia@foxmail.com
# Datetime: 2023/1/31 15:30
# Filename: grad.py
import numpy as np
from matplotlib import pyplot as plt


def f(x):
    return x ** 2 + 1


def g(x):   # f(x)的导数
    return 2 * x


if __name__ == '__main__':
    max_count = 50000
    lr = 0.05
    x_k = np.random.uniform(-1, 1)
    err = 0.00001
    print('Init x_0 is : ', x_k)

    # fig = plt.figure()
    # plt.ion()
    # x_ = np.linspace(-1, 1, num=200)
    # plt.plot(x_, f(x_))

    for i in range(max_count):
        # if 'sca' in globals():
        #     sca.remove()
        # sca = plt.scatter(x_k, f(x_k), s=100, lw=0, c='red', alpha=0.5)
        # plt.pause(0.1)

        grad = g(x_k)  # 计算梯度
        if abs(grad) < err:  # 梯度收敛到控制误差内
            break
        x_k = x_k + (-grad) * lr  # 更新x(迭代公式: 梯度下降法)
        # x_k = x_k - grad / 2  # 更新x(迭代公式: 牛顿法由于是一元二次函数所以其二阶导数为常数2)

    print('The optimal solution x* is: {:.6f} ==> f(x*)={:.6f}'.format(x_k, f(x_k)))

    # plt.scatter(x_k, f(x_k), s=100, lw=0, c='green')
    # plt.ioff()
    # plt.show()

  可视化效果如下

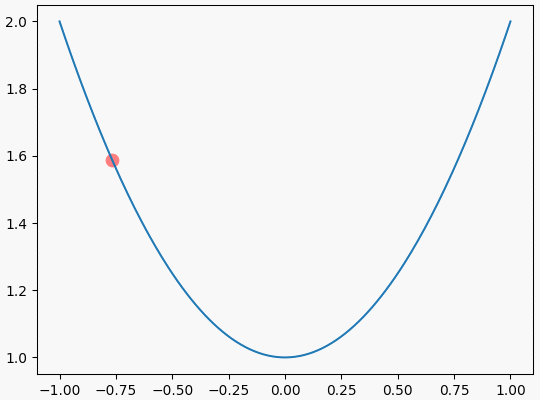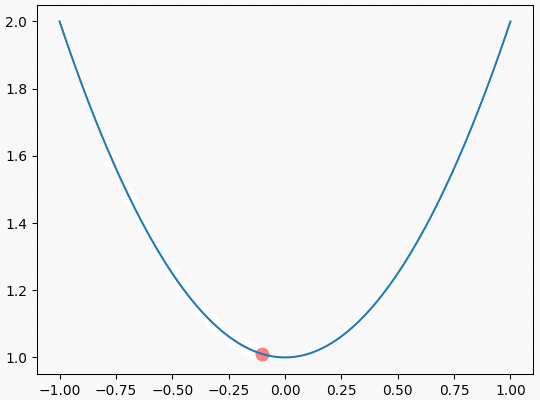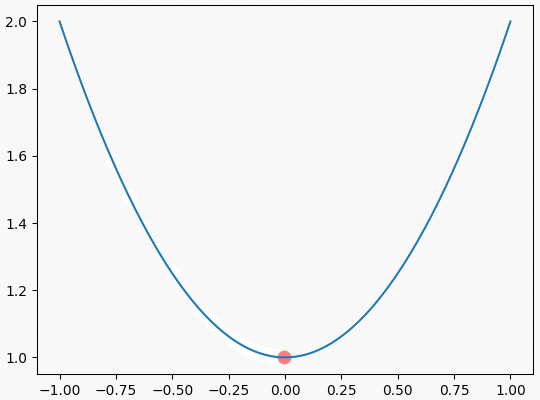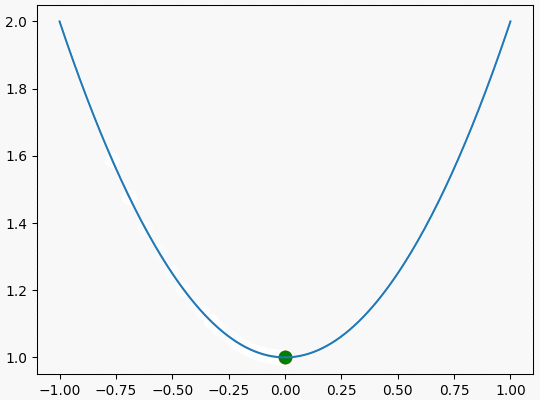
结束语

  持续充电中博客内容也在不断更新补充中如有错误欢迎来私戳小编哦共同进步感谢Thanks♪(･ω･)ﾉ