【机器学习 | 回归问题】超越直线:释放多项式回归的潜力 —— 详解线性回归与非线性 (含详细案例、源码)
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

♂️ 个人主页: @AI_magician
主页地址 作者简介CSDN内容合伙人全栈领域优质创作者。
景愿旨在于能和更多的热爱计算机的伙伴一起成长
♂️声明本人目前大学就读于大二研究兴趣方向人工智能&硬件虽然硬件还没开始玩但一直很感兴趣希望大佬带带

摘要 本系列旨在普及那些深度学习路上必经的核心概念文章内容都是博主用心学习收集所写欢迎大家三联支持本系列会一直更新核心概念系列会一直更新欢迎大家订阅
该文章收录专栏
[✨— 《深入解析机器学习从原理到应用的全面指南》 —✨]
回归问题
线性回归的发展可以追溯到19世纪。以下是一些重要的里程碑
-
1805年卡尔·弗里德里希·高斯Carl Friedrich Gauss提出了最小二乘法的概念为线性回归提供了数学基础。
-
1861年弗朗西斯·高尔顿Francis Galton进行了一项关于遗传与身高之间关系的研究这可以被认为是最早的线性回归应用之一。
-
1897年弗朗西斯·埃杰顿Francis Edgeworth提出了一种用于估计回归系数的方法称为最大似然估计。
-
1922年罗纳德·费舍尔Ronald Fisher提出了最小二乘估计的统计性质并发表了关于线性回归的经典论文。
-
1950年代由于计算机技术的发展线性回归在统计学和经济学中得到广泛应用。
-
1960年代提出了多元线性回归允许模型包含多个自变量。
-
1970年代出现了岭回归和lasso回归等正则化方法用于处理多重共线性和特征选择问题。
-
1990年代至今随着机器学习和统计学的快速发展线性回归仍然是许多预测建模和数据分析任务中的重要方法。同时出现了更复杂的回归模型和非线性回归方法如广义线性模型、多项式回归、支持向量回归等。
线性回归作为一种简单而强大的统计方法在实际应用中得到广泛使用。它被应用于经济学、金融学、社会科学、医学、工程等领域用于建立预测模型、探索变量之间的关系以及进行因果推断。
线性回归
线性回归是一种线性方法用于建立自变量 X X X 和因变量 Y Y Y 之间的线性关系模型这里的X可以是自变量矩阵。这种关系通常形式化为以下等式
Y = β 0 + β 1 X + ϵ Y = \beta_0 + \beta_1X + \epsilon Y=β0+β1X+ϵ
其中 β 0 \beta_0 β0 和 β 1 \beta_1 β1 是模型参数代表截距和斜率 ϵ \epsilon ϵ 是误差项不被训练。
线性回归的目标是找到参数 β 0 \beta_0 β0 和 β 1 \beta_1 β1使得模型预测的 Y Y Y 值与实际 Y Y Y 值之间的残差平方和最小。这被称为最小二乘法。这意味着我们想找到 β ^ 0 \hat{\beta}_0 β^0 和 β ^ 1 \hat{\beta}_1 β^1使得
∑ i = 1 n ( y i − ( β ^ 0 + β ^ 1 x i ) ) 2 \sum_{i=1}^n (y_i - (\hat{\beta}_0 + \hat{\beta}_1 x_i))^2 i=1∑n(yi−(β^0+β^1xi))2
最小其中 ( x i , y i ) (x_i, y_i) (xi,yi) 是第 i i i 个观测值。
下面是如何使用 Python 的 scikit-learn 库进行线性回归的一个例子。在这个例子中我们使用波士顿房价数据集这是一个典型的开源数据集。
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 使用线性回归模型
model = LinearRegression()
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print('Mean Squared Error:', mse)
首先我们导入必要的库和数据集然后划分训练集和测试集。接着我们创建一个线性回归模型实例并使用训练数据对其进行拟合。然后我们使用该模型预测测试数据并计算均方误差来评估模型性能。
多项式回归非线性
多项式回归是一种基于多项式函数的回归分析方法用于拟合非线性关系的数据。它通过引入多项式特征可以拟合更复杂的数据模式。
原理和数学公式推导
假设我们有一个简单的数据集包含一个特征 X 和对应的目标变量 y。我们希望使用多项式回归来拟合这些数据。
多项式回归模型的基本假设是目标变量 y 与特征 X 之间存在一个多项式关系。我们可以用以下公式表示多项式回归模型
y = w0 + w1*X + w2*X^2 + ... + wn*X^n
其中X 是原始特征X^2 表示 X 的平方X^3 表示 X 的立方以此类推。w0, w1, ..., wn 是多项式回归模型的系数需要通过训练拟合得到。
为了使用多项式回归拟合数据我们可以将特征 X 转换为多项式特征。通过引入幂次组合我们可以将原始特征的非线性关系纳入考虑。
具体地我们可以将多项式回归问题转化为普通的线性回归问题。将多项式特征表示为新的特征向量 X_poly然后使用线性回归模型进行训练。将对应的多项式特征即幂方组合当成多元线性来求解
为了将特征 X 转换为多项式特征我们可以使用 PolynomialFeatures 类。它可以生成包含原始特征幂次组合的新特征矩阵。
训练多项式回归模型的步骤如下
- 准备数据集将原始特征
X和目标变量y划分为训练集和测试集。 - 特征转换使用
PolynomialFeatures类将训练集和测试集的特征X转换为多项式特征。可以指定多项式的次数degree 参数。
假设我们有一个简单的数据集包含一个特征x和对应的目标变量y。原始数据如下
x = [1, 2, 3] y = [2, 4, 6]使用PolynomialFeatures
[[1 1 1] [1 2 4] [1 3 9]]可以看到使用PolynomialFeatures对特征x进行多项式扩展后生成了3列特征。第一列是常数项1第二列是原始特征x第三列是x的平方。这样我们就得到了一个包含3个特征的新数据集x_poly。
当面对多个特征时在多个特征上使用PolynomialFeatures。
假设我们有一个包含两个特征x1和x2的数据集以及对应的目标变量y。原始数据如下
x1 = [1, 2, 3] x2 = [4, 5, 6] y = [10, 15, 20]的到如下
[[ 1 1 4 1 4 16] [ 1 2 5 4 10 25] [ 1 3 6 9 18 36]]可以看到使用PolynomialFeatures对特征x1和x2进行多项式扩展后生成了6列特征。第一列是常数项1接下来两列是原始特征x1和x2然后是两列特征的乘积最后两列是各特征的平方。这样我们就得到了一个包含6个特征的新数据集x_poly。
- 训练模型使用线性回归模型如
LinearRegression对转换后的训练集进行训练。模型会学习多项式回归方程的系数。 - 预测使用训练好的模型对转换后的测试集进行预测。
- 评估通过比较预测结果与实际目标变量的值评估多项式回归模型的性能。
经典案例
以下是一个使用多项式回归拟合波士顿房价的经典案例的 Python 代码实现。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.pipeline import Pipeline
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 管道
pipeline = Pipeline([
("PolynomialFeatures", PolynomialFeatures(degree=2)),# 多项式特征转换
("LinearRegression",LinearRegression())# 线性回归模型训练
])
pipeline.fit(X_train, y_train)
# 预测结果
y_pred = pipeline.predict(X_test)
# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
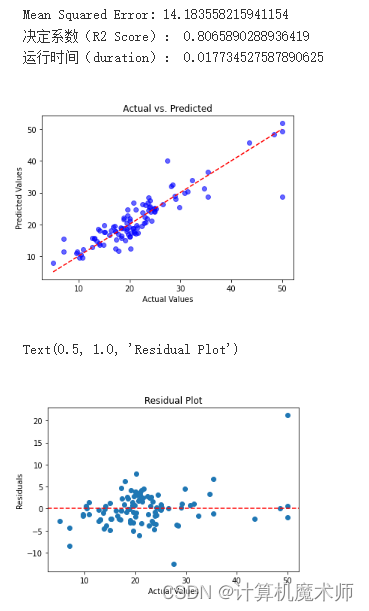
print('Mean Squared Error:', mse)
plt.scatter(y_test, y_pred, c='blue', alpha=0.6)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--') # 绘制对角线
plt.title('Actual vs. Predicted')
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.show()
# 计算残差
residuals = y_test - y_pred
# 绘制残差图
plt.scatter(y_test, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Actual Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
相关学习文档或优秀博客
以下是一些关于多项式回归的学习资源和优秀博客可以帮助你更深入地理解多项式回归算法和其应用
SLSQP 优化训练算法
SLSQPSequential Least Squares Programming算法是一种用于求解带有约束条件的非线性优化问题的算法。它是一种迭代算法通过不断迭代来逼近问题的最优解。下面我将详细介绍SLSQP算法的整体流程并以优化带有约束条件的多项式为例进行说明。
SLSQP算法的整体流程如下
-
确定优化目标函数和约束条件首先需要明确需要优化的目标函数和约束条件。在本例中我们假设我们要最小化一个多项式函数同时满足一些约束条件。
-
初始化给定初始解可以是随机选择的或者根据问题的特点选择的一个可行解。
-
构建拉格朗日函数将目标函数和约束条件结合起来构建拉格朗日函数。拉格朗日函数是由目标函数和约束条件通过引入拉格朗日乘子所得到的一个函数。
-
求解子问题通过求解拉格朗日函数的子问题来更新变量的值。子问题是通过将拉格朗日函数对变量进行最小化求解得到的。
-
更新约束条件根据当前变量的值更新约束条件。如果约束条件中包含不等式约束可能需要使用一些方法来将其转化为等式约束。(引入罚函数或者松弛变量运筹学)
-
判断终止条件判断当前解是否满足终止条件。终止条件可以是达到一定的迭代次数、目标函数的变化量小于某个阈值或者满足约束条件的程度达到一定的要求等。
-
迭代更新如果终止条件不满足则返回第4步继续迭代更新。
-
输出结果当终止条件满足时输出最优解的变量值以及对应的目标函数值。
以上是SLSQP算法的整体流程。下面我们以优化带有约束条件的多项式为例进行说明。
假设我们要最小化一个二次多项式函数 f(x) = x^2 + 2x + 1同时满足约束条件 g(x) = x >= 0。
- 确定优化目标函数和约束条件目标函数为 f(x) = x^2 + 2x + 1约束条件为 g(x) = x >= 0。
- 引入罚函数将不等式约束转化为罚函数惩罚项即将原始的不等式约束 g(x) = x >= 0 转化为 g(x) - ρ其中 ρ 是罚函数的惩罚参数通常为非负数。
- 初始化选择一个初始解例如 x = 0。
- 构建拉格朗日函数构建拉格朗日函数 L(x, λ) = f(x) + λ*g(x)其中 λ 是拉格朗日乘子。
- 求解子问题通过最小化拉格朗日函数 L(x, λ) 对 x 进行求解得到更新后的 x 值。
- 更新约束条件根据当前的 x 值和约束条件 g(x) 的情况更新罚函数参数 ρ。通常情况下如果当前解满足约束条件可以减小 ρ 的值以使罚函数的惩罚项对目标函数的影响减小如果当前解不满足约束条件可以增大 ρ 的值以加大罚函数的惩罚项。
- 判断终止条件判断当前解是否满足终止条件例如目标函数的变化量小于某个阈值。
- 迭代更新如果终止条件不满足返回第4步继续迭代更新。
- 输出结果当终止条件满足时输出最优解的变量值以及对应的目标函数值。
通过以上流程我们可以使用SLSQP算法找到满足约束条件下的多项式的最小值。需要注意的是实际应用中可能需要根据具体问题对SLSQP算法进行一些调整和优化以提高求解效率和准确性。
代码案例
我们首先需要目标函数和损失函数,所以需要先定义以实现
import numpy as np
from sklearn.datasets import load_boston
from sklearn.preprocessing import PolynomialFeatures
from scipy.optimize import minimize
from sklearn.metrics import mean_squared_error, r2_score
from time import time
start = time()
# 加载波士顿数据集
boston = load_boston()
X = boston.data # 特征矩阵
y = boston.target # 目标变量
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42)
# 创建PolynomialFeatures对象生成多项式特征
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X_train)
# 定义损失函数均方误差
def loss_function(theta):
y_pred = np.dot(X_poly, theta)
mse = mean_squared_error(y_train, y_pred)
return mse
# 定义约束条件无约束
constraints = ()
# 定义优化问题 初始参数x0全零向量
optimization_problem = minimize(loss_function, x0=np.zeros(X_poly.shape[1]), constraints=constraints, method='SLSQP')
# 获取优化结果
theta_optimized = optimization_problem.x
# 在测试集上进行预测
X_test_poly = poly_features.transform(X_test)
y_pred = np.dot(X_test_poly, theta_optimized)
# 计算测试集上的均方误差和决定系数
mse_train = mean_squared_error(y_test, y_pred)
r2_train = r2_score(y_test, y_pred)
# 输出结果
print("多项式回归模型拟合结果")
print("均方误差MSE", mse_train)
print("决定系数R2 Score", r2_train)
print("运行时间duration", time() - start)
plt.scatter(y_test, y_pred, c='blue', alpha=0.6)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--') # 绘制对角线
plt.title('Actual vs. Predicted')
plt.xlabel('Actual Values')
plt.ylabel('Predicted Values')
plt.show()
# 计算残差
residuals = y_test - y_pred
# 绘制残差图
plt.scatter(y_test, residuals)
plt.axhline(y=0, color='r', linestyle='--')
plt.xlabel('Actual Values')
plt.ylabel('Residuals')
plt.title('Residual Plot')
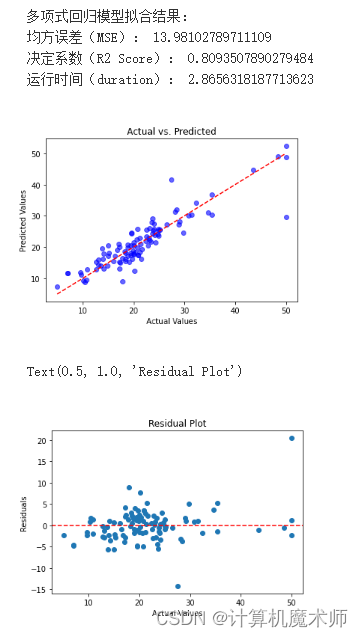
可以看时间是比较久的整体精度更高但是时间较慢还有便是该算法在面对非常数据能够有着非常良好的效果比如六个点拟合带约束

到这里如果还有什么疑问
欢迎私信博主问题哦博主会尽自己能力为你解答疑惑的
如果对你有帮助你的赞是对博主最大的支持
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

