15. 机器学习 - 支持向量机-CSDN博客
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

Hi, 你好。我是茶桁。
逻辑回归预测心脏病
在本节课开始呢我给大家一份逻辑回归的练习利用下面这个数据集做了一次逻辑回归预测心脏病的练习。
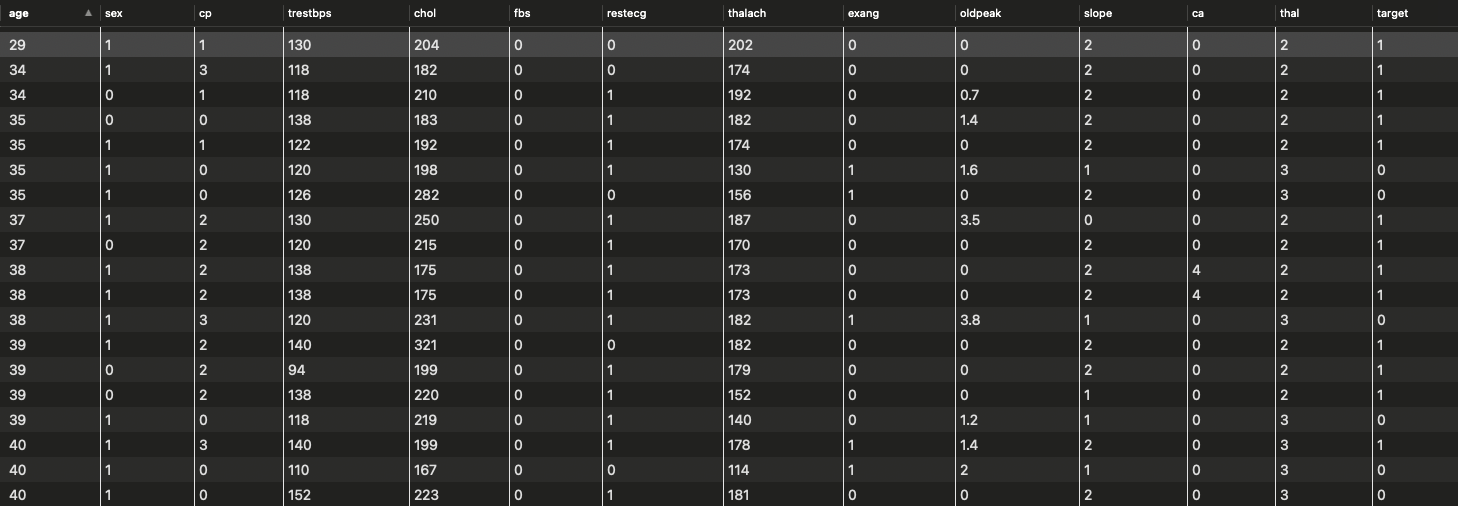
本次练习的代码在「茶桁的AI秘籍」在Github上的代码库内数据集的获取在文末。这样做是因为我的数据集都是和百度盘同步的很多数据集过大了所以也就不传Github了。而且我直接获取盘内同步数据也更方便。
还有一个原因有些数据集可能以后会收费获取。
好让我们进入今天的正课。
因为未来几节课的内容比较多。「核心基础」的这部分内容已经超出我原本的预计咱们「核心基础」的部分刚刚过半可是已经写到15节了本来这部分内容我是想在21节左右结束的所以我们还是要压缩一下内容了。
这节课咱们还是继续讲解经典的机器学习。
支持向量机
接下来要讲解一个非常有趣的方法支持向量机。
支持向量机的原理其实可以很复杂但它是一个很经典的思想方法。咱们就把它的核心思想讲明白就行了。其实我们平时在工作中用的也比较少。但是面试中有一些老一代的面试官会比较喜欢问这个问题。
支持向量机的核心思想假如我们有两堆数据希望找一根线去把它做分类那么咱们找哪一根线呢
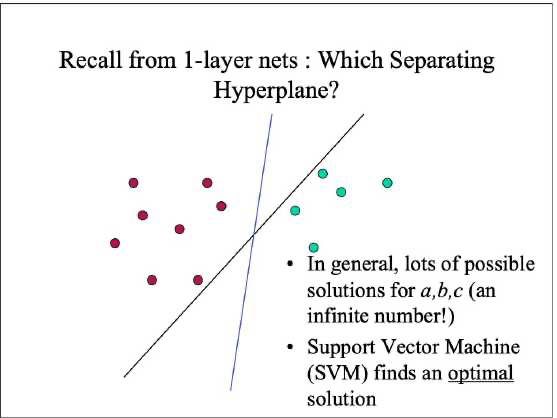
上图中我们假设黑色的那根线定义为l把离这根线最近的点也就是直线距离最小的点找到两个这样的点定义为P1、P2。
现在我们是希望离这个l最近的点假如说是d1,d2那么我们希望这两个距离加起来最大max|d1+d2|。
现在再定义蓝色的线为直线b那直线b做分类就比直线l要好。为什么直线b就比是直线l好呢? 因为直线b离d1,d2普遍都比较远。
现在这里的演示是一个二维平面中用一根线来分割如果是在多维空间中SVM的目标就是找到一个最佳的超平面来最大化间隔同时确保正确分类样本。
假设我们有一组训练样本每个样本用特征向量x表示并且标记为正类别+1或负类别-1。
我们可以表示为以下凸优化问题
m i n w , b 1 2 ∣ ∣ w ∣ ∣ 2 \begin{align*} min_{w, b}\frac{1}{2}||w||^2 \end{align*} minw,b21∣∣w∣∣2
其中对所有样本
y i ( w ⋅ x i + b ) ≥ 1 y_i(w \cdot x_i+b) \ge 1 yi(w⋅xi+b)≥1
w是超平面的法向量b是截距项yi是样本xi的标签也就是+1或者-1。
为了解决这个优化问题我们引入拉格朗日乘子 a i a_i ai来得到拉格朗日函数
L ( w , b , a ) = 1 2 ∣ ∣ w ∣ ∣ 2 − ∑ i = 1 N a i [ y i ( w ⋅ x i + b ) − 1 ] L(w,b,a) = \frac{1}{2}||w||^2 - \sum_{i=1}^Na_i[y_i(w\cdot x_i +b) - 1] L(w,b,a)=21∣∣w∣∣2−i=1∑Nai[yi(w⋅xi+b)−1]
然后我们要最小化拉格朗日函数首先对w和b求偏导数令它们等于0然后代入拉格朗日乘子条件:
a i [ y i ( w ⋅ x i + b ) − 1 ] = 0 a_i[y_i(w\cdot x_i + b)-1] = 0 ai[yi(w⋅xi+b)−1]=0
然后我们就可以得到如下这个式子
w = ∑ i = 1 N a i y i x i s u m i = 1 N a i y i = 0 w = \sum_{i=1}^Na_iy_ix_i \\ sum_{i=1}^N a_iy_i = 0 w=i=1∑Naiyixisumi=1Naiyi=0
使用某种优化算法例如SMO算法求解拉格朗日乘子 a i a_i ai。我们就可以使用求解得到的 a i a_i ai计算超平面参数w和b。
对于新样本x使用超平面 w ⋅ x + b w\cdot x + b w⋅x+b的符号来预测其类别。
那我们讲了这么半天都是一个支持向量机的数学演示过程下面我们来看看具体的代码实现。
我们先来生成两组数据这两组数据咱们让他距离更大
import numpy as np
label_a = np.random.normal(6, 2, size=(50, 2))
label_b = np.random.normal(-6, 2, size=(50, 2))
我们现在来观察以下生成的这些点
import matplotlib.pyplot as plt
plt.scatter(*zip(*label_a))
plt.scatter(*zip(*label_b))
plt.show()
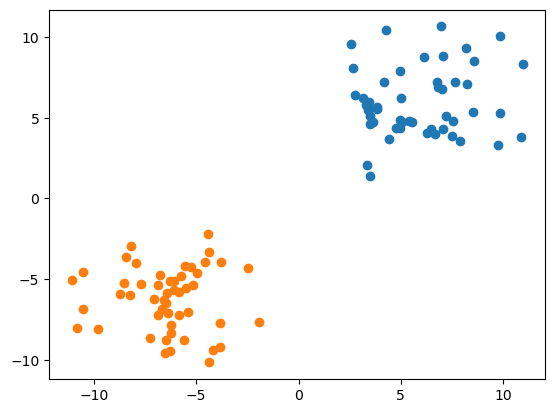
然后我们继续
label_a_x = label_a[:, 0]
label_b_x = label_b[:, 0]
我们就将这两组数据的第一列分别取出来了。
接着我们随机的定义一些w和b
for i in range(100):
w, b = (np.random.random(size=(1, 2)) * 10 - 5)[0]
然后我们按照之前讲的数学演示来定义一个函数
def f(x):
return w*x+b
然后我们之前从数学演示里已经知道 y i ( w ⋅ x + b ) ≥ 1 y_i(w\cdot x+b) \ge 1 yi(w⋅x+b)≥1, 而我们也知道这个说的是距离也就是说同样的$y_i(w\cdot x+b) \le -1 $。
也就是说我们要让函数f小于等于-1并且大于等于1。当然为了保证其被分到两边我们将函数的最大值定义为小于等于-1 将函数的最小值定义为大于等于1。这样就保证(-1,1)之间是不存在任何函数值
np.max(f(label_a_x, w, b)) <= -1 and np.min(f(label_b_x, w, b)) >= 1
只有同时满足这两个条件的值我们才会留下来进行保存。我们可以定义一个变量将其保存
w_and_b = []
for i in range(100):
w, b = (np.random.random(size=(1, 2)) * 10 - 5)[0]
if np.min(f(label_a_x, w, b)) >= -1 and np.min(f(label_b_x, w, b)) >= 1:
w_and_b.append((w, b))
在得到这些w,b之后我们将这些w,b连起来进行画图
for w, b in w_and_b:
x = np.concatenate((label_a_x, label_b_x))
plt.plot(x, f(x, w, b))
plt.show()
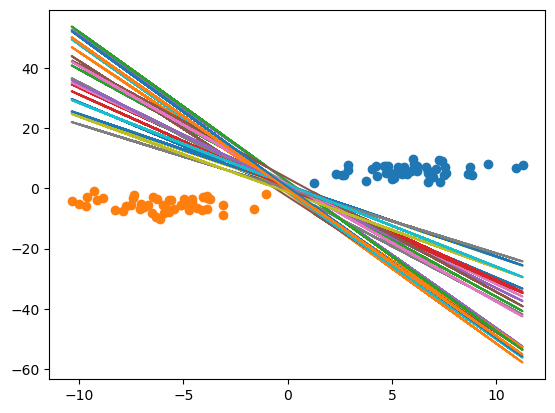
这样我们就拟合出来了很多的曲线。这些个曲线到底哪一个是最好的那一个呢
现在根据刚刚得到的那个结论现在所有的 y i ( w ⋅ x i + b ) y_i(w\cdot x_i + b) yi(w⋅xi+b), 那么现在其实就是 m a r g i n = 2 ∣ ∣ w ∣ ∣ margin = \frac{2}{||w||} margin=∣∣w∣∣2。
那我们现在就找这个w最小的这个值就可以了。
w, b = min(w_and_b, key = lambda w_b: w_b[0])
all_x = np.concatenate((label_a_x, label_b_x))
plt.plot(all_x, f(all_x, w, b), 'r-o')
plt.show()
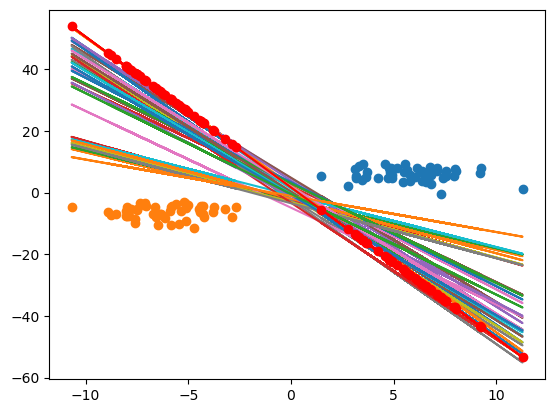
现在我们就可以看到那个最优的直线了就是众多红色的点连接起来的那根线。
当然最后代码执行顺序和讲解顺序有一些不一样为了避免数据每次重新生成造成的差别所以最开始是生成数据之后是定义函数、过滤参数以及生成图像。
这个就是支持向量机的原理我们找到离它所有的点的一个距离让它这个边距最大最后得到一个简化结果。
核函数
然后我们再来看另外一个点「核函数」
核函数是支持向量机里面非常重要的一个东西。
如果支持向量机只要数据是线性可分的那么我们一定能够找到它的分割线。但是在实际的现实生活中有很多点并不是线性可分的。
举个例子我们来画一张图
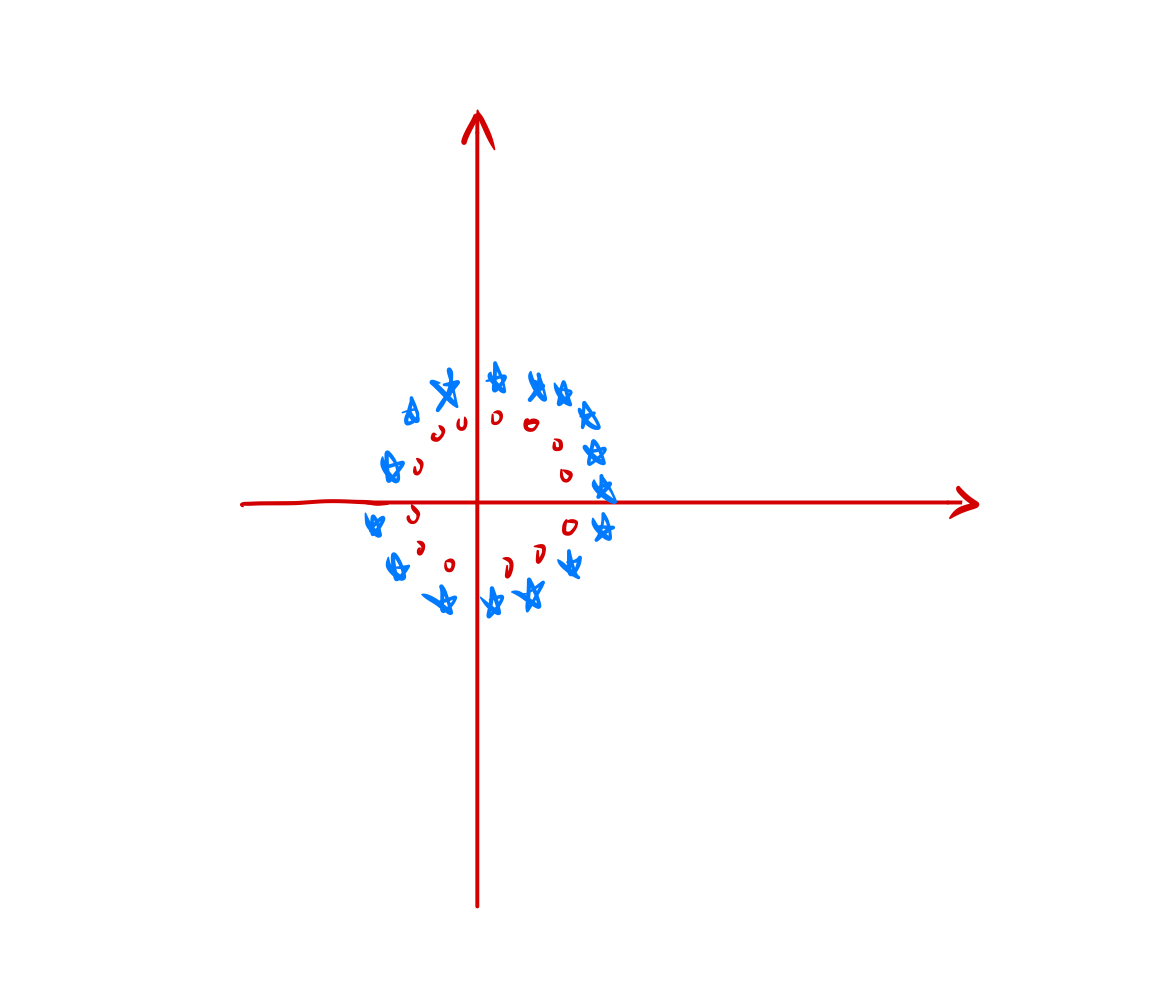
就比如图中的这种数据是无论如何用一条直线无法分割的不管怎么画都无法把蓝色和红色的点分割开。
就像我们下面这张图
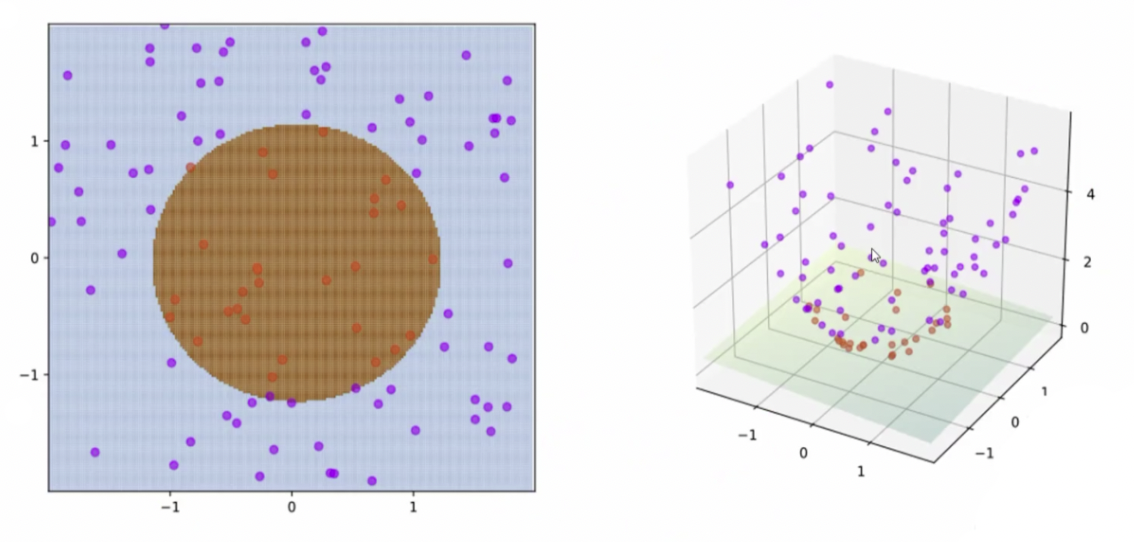
但是我们我们可以做这样一件事情假设我们在一个坐标轴上拥有8个点A、B、C、D为一组a,b,c,d为一组。如下图
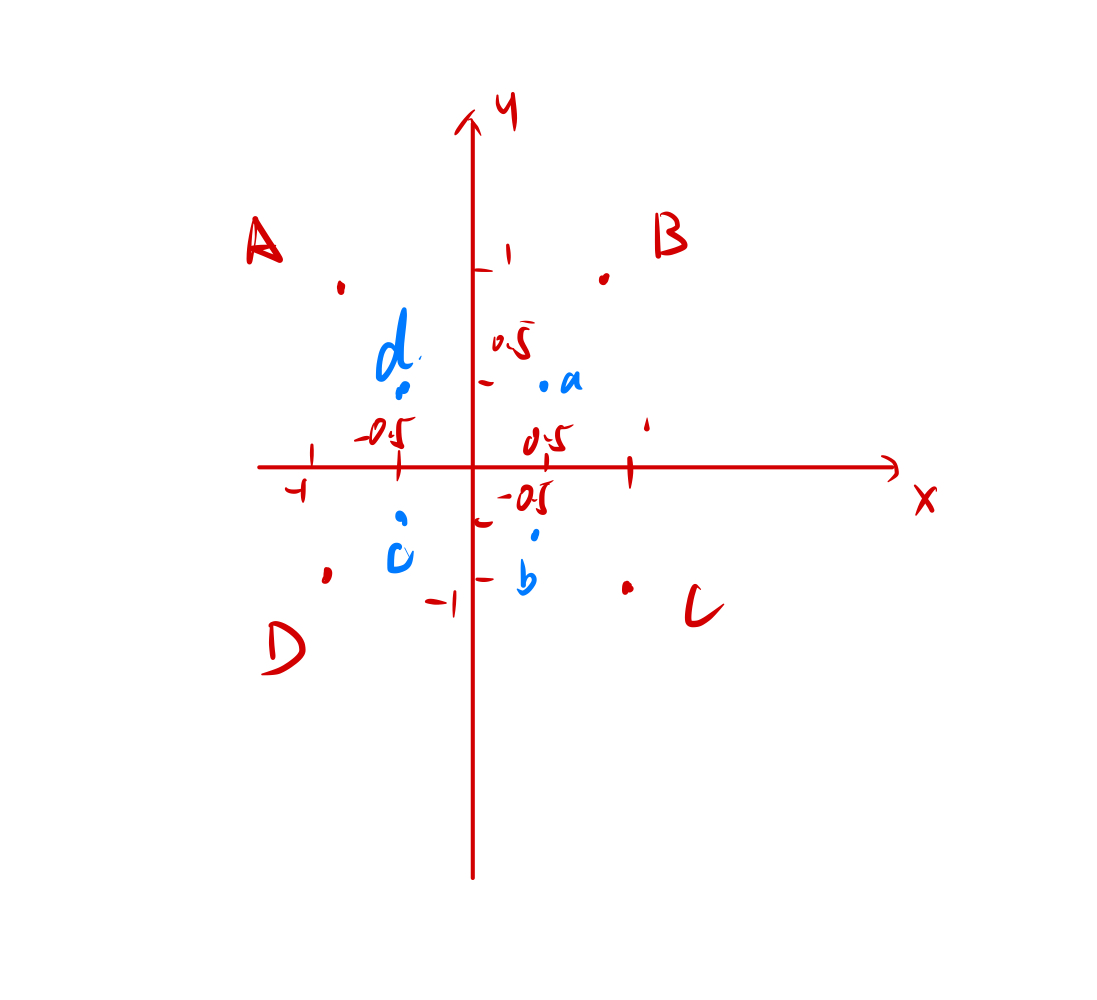
分别为A(-1,1), B(1,1), C(1, -1), D(-1,-1) a(-0.5, 0.5), b(0.5, 0.5), c(0.5, -0.5), d(-0.5, -0.5)。
现在我们ABCD和abcd是无法用一根直线来分割的然后我们令:
f ( x ) = > { x 2 y 2 } \begin{align*} f(x) => \begin{Bmatrix} x^2 \\ y^2 \end{Bmatrix} \end{align*} f(x)=>{x2y2}
那在这种情况下八个点分别就变成了A(1, 1),B(1, 1),C(1, 1),D(1, 1) a(0.25, 0.25),b(0.25, 0.25),c(0.25, 0.25),d(0.25, 0.25)。
那这样的情况下我们就完全可以用一根直线去分割了
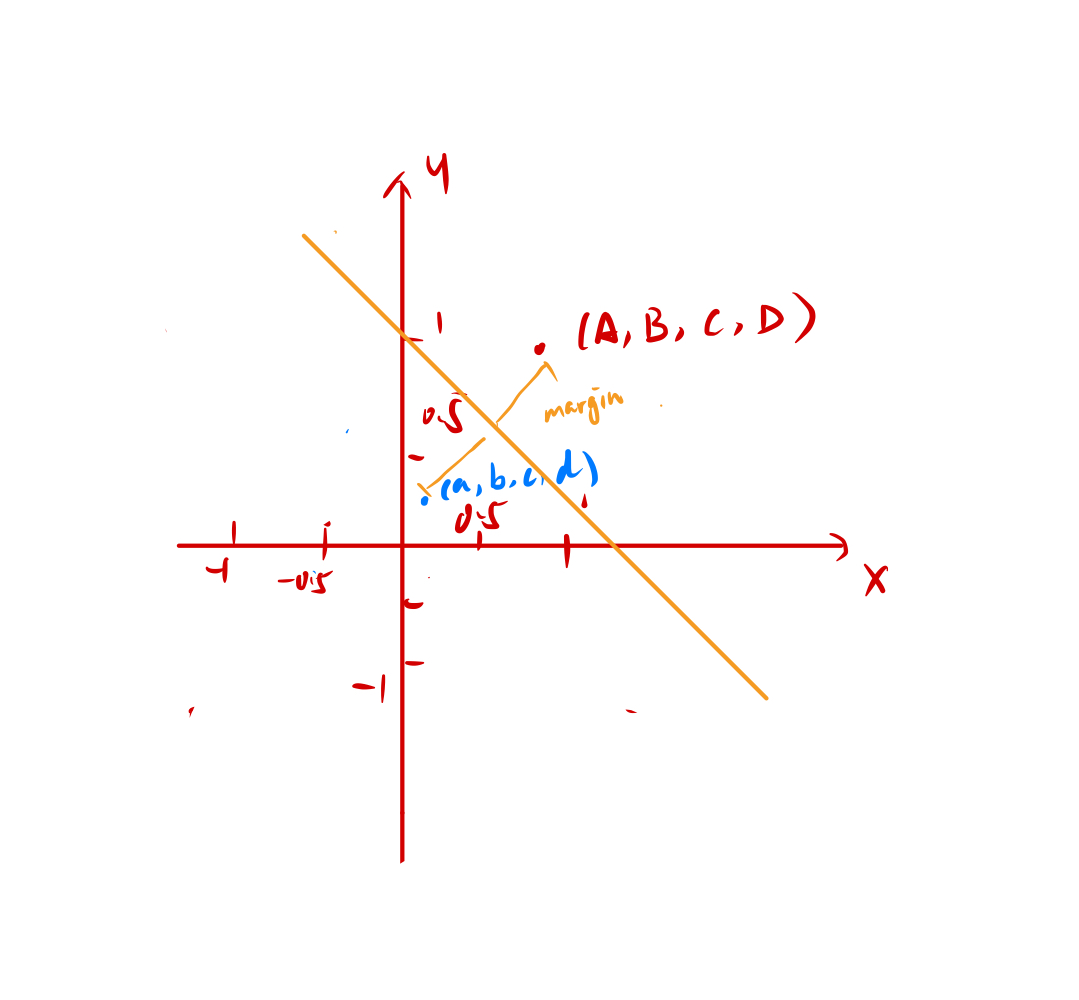
那现在找到这根线是w2 = wx+b那我们遇到新数据应用到这个函数里边再应用到这个线里面做分割就可以了。我们把原本线性不可分的东西变成线性可分的。那么这个就是核函数神奇的地方。
支持向量机通过某非线性变换 φ(x) 将输入空间映射到高维特征空间。特征空间的维数可能非常高。如果支持向量机的求解只用到内积运算而在低维输入空间又存在某个函数 K(x, x′) 它恰好等于在高维空间中这个内积即K(x, x′) =φ(x)⋅φ(x’) ; 。那么支持向量机就不用计算复杂的非线性变换而由这个函数K(x, x′) 直接得到非线性变换的内积使大大简化了计算。我们就将这种函数函数 K(x, x′) 称为核函数。
φ ( x ) = [ x x 2 x 3 ] \varphi (x) = \begin{bmatrix} x \\ x^2 \\ x^3 \end{bmatrix} φ(x)= xx2x3
那其实就类似的事情已经有人总结了一些相应的公式来使用
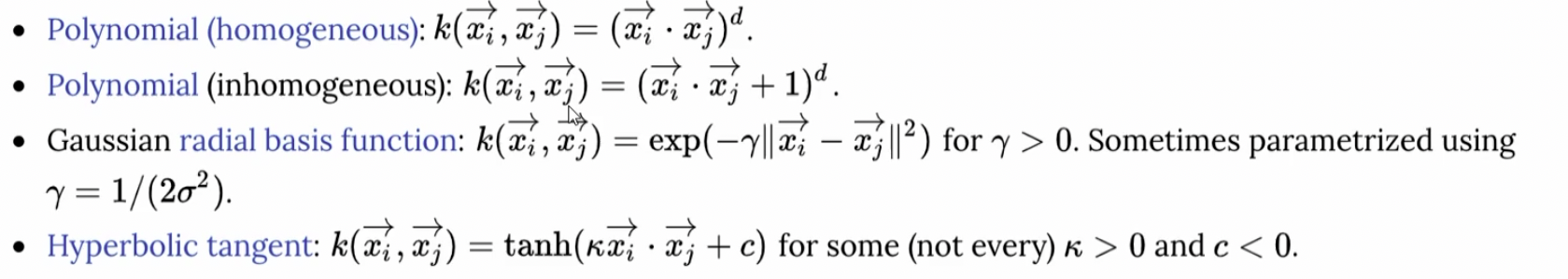
这些是一些常见的核函数。
一般在使用的时候调用它就可以如果在用SVM的时候它会有一个参数。可以自己定义一个核函数但一般不自己定义调用现有的就够了。
SVM其实也有弊端当数据量很复杂的时候现有的核函数就没有作用了。因为它会失效所以我们需要很多的人工分析整个效率很低。
但是在整个机器学习的发展史上它曾经有非常重要的一段历史。有一段时间它的论文量非常的多做科研的非常爱做SVM不是因为快速是因为可以提出来各种各样的Kerno函数。
假如有一组数据不好分割但是你提出了一种新的核函数这个函数量可以比较复杂啊
然后提升了分割率提高了效果。
但是这种方法其实曾经一度让机器学习非常不受人待见在学术圈非常不受人待见。搞机器学习的人就是每天就是发论文说我的曲线比你的曲线强这就是他们干的事。
所以10年左右做机器学习、做人工智能的人都不说自己是做机器学习做人工智能的。都换个名字说做文本挖掘等等。
SVM因为要做各种升维当数据量比较大的时候计算量非常的复杂计算需求量非常的大。
但是SVM它有个好处就是它比较直观还有就是SVM对于不平衡的数据比较有用。
好这节课我们就讲到这里下一节课我们来看「决策树」。
链接: https://pan.baidu.com/s/1Rl8xkQG4c-XSjL6cB4B1XQ?pwd=e8wi 提取码: e8wi 复制这段内容后打开百度网盘手机App操作更方便哦
–来自百度网盘超级会员v6的分享
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |

