【蓝桥杯】简单数论——GCD&LCM

阿里云国内75折回扣微信号：monov8

阿里云国际，腾讯云国际，低至75折。AWS 93折免费开户实名账号代冲值优惠多多微信号：monov8 飞机：@monov6

GCD

最大公约数Greatest Common Divisor(GCD)整数a和b的GCD是指能同时整除a和b的最大整数记为gcd(a,b)。由于-a的因子和a的因子相同因此gcd(a, b)= gcd(al, |bl)。编码时只关注正整数的最大公约数。

GCD性质

(1) gcd(a, b)= gcd(a, a+b)= gcd(a, k·a+b)

(2 gcd(ka,kb)=kgcd(a,b)
(3定义多个整数的最大公约数:gcd(a, b, c)= gcd(gcd(a, b),c)。
(4若gcd(a, b)= d则gcd(a/d, b/d)= 1即a/d与b/d互素。这个定理很重要。
(5) gcd(a+cb, b)= gcd(a, b)

Python库函数gcd()和手写代码

Python函数gcd()

gcd()不会返回负数 ( c++函数std::_gcd()可以返回负数)
gcd()可以带多个参数

from math import *
print(gcd(15,81))        # 3

# 0与其他数b的最大公约数没有意义但会输出b
print(gcd(0,44))         # 44
print(gcd(0,0))          # 0

print(gcd(-6,-15))       # 3  所有数的最大公约数都是正数
print(gcd(-17,289))      # 17
print(gcd(17,-289) )     # 17
print(gcd(48,96,120,688))# 8 多个数的公约数

手写GCD代码

手写gcd函数常用欧几里得算法。
辗转相除法求gcdgcd(a,b) = gcd (b,a mod b) mod取余
这是最常用的方法极为高效。
设a > b辗转相除法的计算复杂度为O( $log_2a^3$ )。

可能输出负数和库函数不同。若不需要输出负数可以将第二行代码的a改成abs(a)。

注意一次只能求两个数的最小公倍数求n个数的需要求n-1次。

def gcd(a, b):
    if b==0: return a # 不需要输出负数可以将a改成abs(a)
    else:    return gcd(b, a%b)
print(gcd(15,81))  # 3

# 第二个数为负数才输出负数
print(gcd(-6,-15)) # -3
print(gcd (-17,289))# 17
print(gcd(17,-289)) # 17

LCM

最小公倍数LCM ( the Least Common Multiple 。
a和b的最小公倍数lcm(a, b)从算术基本定理推理得到。
算术基本定理:任何大于1的正整数n都可以唯一分解为有限个素数的乘积: $n=p_1^{c1}p_2^{c2}...p_m^{cm}$ 其中 $c_i$ 都是正整数 $p_i$ 都是素数且从小到大。

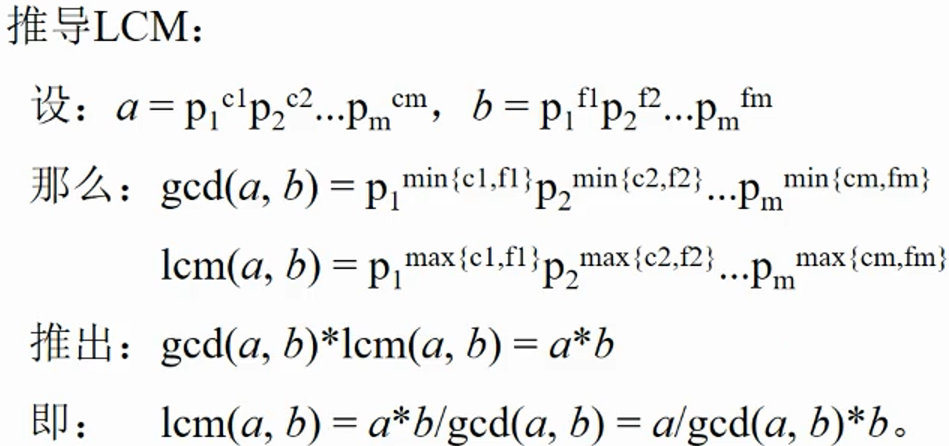
结论lcm(a,b) = a*b/gcd(a,b) = a/gcd(a,b)*b c++先除后乘避免溢出

Python库函数lcm()和手写代码

1、库函数lcm()

在Python新版本(Python3.9才加入了lcm中有库函数lcm()它可以带多个参数。

from math import *
print(lcm(3,6,8,9))  # 72

2、手写lcm()

在Python的旧版本中并没有lcm()函数自己写一个lcm():

from math import *
def lcm(x, y):
    return x*y//gcd(x, y)

例题一核桃的数量

2013年第四届省赛lanaiaoOJ题号210

题目描述

小张是软件项目经理他带领 3 个开发组。工期紧今天都在加班呢。为鼓舞士气小张打算给每个组发一袋核桃据传言能补脑。他的要求是

各组的核桃数量必须相同

各组内必须能平分核桃当然是不能打碎的

尽量提供满足 1,2 条件的最小数量节约闹革命嘛

输入描述

输入一行 a,b,c都是正整数表示每个组正在加班的人数用空格分开(a,b,c<30)。

输出描述

输出一个正整数表示每袋核桃的数量。

输入输出样例

输入
2 4 5
输出
20

简单题答案就是三个数字的最小公倍数。

from math import*
def lcm(x, y):
    return x//gcd(x, y)*y
a,b,c = map(int,input ().split())
k = lcm(a, b)
print(lcm(k,c))

例题二等差数列

2019年第十届省赛lanqiao0J题号192

题目描述

数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列只记得其中 N 个整数。

现在给出这 N 个整数小明想知道包含这 N 个整数的最短的等差数列有几项

输入描述

输入的第一行包含一个整数 N。

第二行包含 N 个整数 1,2,⋅⋅⋅,A1,A2,⋅⋅⋅,AN。(注意 A1 ∼ AN 并不一定是按等差数列中的顺序给出)

其中2≤N≤ $10^5$ 0≤ $A_i$ ≤ $10^9$ 。

输出描述

输出一个整数表示答案。

输入输出样例

输入
5
2 6 4 10 20
输出
10
样例说明包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、 18、20。

思路

所有数字间距离最小的间隔是公差吗?
并不是例如{257}最小的间隔是2但公差不是2是1。
间隔的最小公因数是公差这是gcd问题。把n个数据排序计算它们的间隔对所有间隔做GCD结果为公差。
最少数量等于(最大值-最小值) / 公差+1。

from math import *
n = int (input())
a = list(map(int,input().split() ))
a. sort () # 原地排序
d = 0
for i in range (1, n):
    d = gcd (d, a[i]-a[i-1])
if d == 0:            # 公差为0
    print (n)
else:
    print((a[-1]-a[0])//d + 1)

例题三、 Hankson的趣味题

Hankson的趣味题 lanqiao0J题号520

题目描述

在课堂上老师讲解了如何求两个正整数 c1 和 c2 的最大公约数和最小公倍数。现在 Hankson 认为自己已经熟练地掌握了这些知识他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”这个问题是这样的已知正整数 a0,a1,b0,b1设某未知正整数 x 满足

x 和 a0 的最大公约数是 a1

x 和 b0 的最小公倍数是 b1。

Hankson 的“逆问题”就是求出满足条件的正整数 x。但稍加思索之后他发现这样的 x 并不唯一甚至可能不存在。因此他转而开始考虑如何求解满足条件的 x 的个数。请你帮助他编程求解这个问题。

输入描述

第一行为一个正整数 n表示有 n 组输入数据。

接下来的 n 行每行一组输入数据为四个正整数 a0a1b0b1每两个整数之间用一个空格隔开。输入数据保证 a0 能被 a1 整除b1 能被 b0 整除。

其中保证有 1≤a0a1b0b1≤2× $10^9$ 且n≤2000。

输出描述

输出共 n 行。每组输入数据的输出结果占一行为一个整数。

对于每组数据若不存在这样的 x请输出 0若存在这样的 x请输出满足条件的 x 的个数

输入输出样例

输入
2
41 1 96 288
95 1 37 1776 
输出
6
2

问题解析

1、暴力法

from math import *
def lcm(x, y):
    return x//gcd(x, y)*y

n = int(input())
for i in range(n):
    ans = 0
    a0,a1,b0,b1 = map(int,input().split())
    for x in range(1,b1+1):                  # x的最大可能值为b1
        if gcd (x, a0)==a1 and lcm(x, b0)==b1:
            ans +=1
    print(ans)

本题n≤2000x的范围:x≤b1而b1≤2× $10^9$ O(n*b1)=4* $10^{12}$ 超过蓝桥杯规定的 $10^8$ 故超时了。

2、优化

若x是b1的因子有x*y = b1y也可能是答案。
只需要在范围x<=sqrt(b)内查询同时判断y就行了。
但还是超时因为gcd计算也要花时间加上一个优化: if b1%x==0表示b1是x的公倍数。

from math import*
def lcm(x, y):
    return x//gcd (x, y)*y
n = int(input ())
for _ in range (n):
    a0, a1, b0, b1 = map(int, input().split())
    ans = 0
    for x in range(1,int(sqrt(b1))+1):
        if b1 % x ==0:      #若b1是x的公倍数
            if gcd(x, a0) ==a1 and lcm(x, b0)==b1: ans+=1
            y = b1//x
            if x==y : continue    # 重复了跳过
            if gcd(y, a0)==a1 and lcm(y, b0)==b1: ans+=1
    print(ans)

例题四最大比例

2016年第七届省赛lanqiao0J题号120

题目描述

X 星球的某个大奖赛设了 M 级奖励。每个级别的奖金是一个正整数。并且相邻的两个级别间的比例是个固定值。也就是说所有级别的奖金数构成了一个等比数列。比如16,24,36,54其等比值为3/2

现在我们随机调查了一些获奖者的奖金数。请你据此推算可能的最大的等比值。

输入描述

第一行为数字 N (0<N<100)表示接下的一行包含 N 个正整数

第二行 N 个正整数 Xi(Xi<109)用空格分开。每个整数表示调查到的某人的奖金数额

输出描述

一个形如 A/B 的分数要求 A、B 互质。表示可能的最大比例系数测试数据保证了输入格式正确并且最大比例是存在的。

输入输出样例

输入
3
1250 200 32
输出
25/4

思路

把这些数字排个序然后算出相邻两个数的比值。
最小的那个比值K是否就是答案呢?
不是。例如{2,16, 64}比值是16/2=864/16=4最小比值K=4。但原序列是{2,4,8,16,32,64}比值是2。
答案可能比K小如何求出答案?如果一个个试比K小的分数肯定会超时。

换一个思路

不是算相邻两个数的比值而是每个数对第一个数的比值。
设原序列是 $\{x,xq^{1},xq^2...,q^{n-1}\}$ ,q为公比从中挑出一些数字 $\{xq^c,xq^{d}...,xq^{y},xq^z\}$ ,它们之间的两两相除得到一个比值序列 $\{1,q^{d-c},...,q^{z-y}\}$ 这其中的一些数字可能是相同的。算它们对第一个数的比值得 $\{1,q^{d-c},...,q^{y-c},q^{z-c}\}$ $=\{1,q^{kd},...,q^{ky},q^{qkz}\}$ 这个序列内的所有数字肯定不同。
令q= a/b这个序列变成了 $\{1, (a/b)^{kd}, .... (a/b)^{ky}, (a/b)^{kz}\}$
分成分子和分母两个序列分别是 $A=\{a^{kd},...,a^{ky}, a^{kz}\}, B=\{ b^{kd}, .... b^{ky}, b^{kz}\}$ 。
已知这两个序列A、B中每个元素的值求a和b。

举例A={16,128,512,1024}得a=2即 $A=\{2^{4},2^{7},2^{9},2^{10}\}$

如何根据A求a?
显然A中每个数除以前面一个数都能够整除得到a的一个倍数但是这个倍数还不是a需要继续除直到系列中出现1为止就得到a。以前2个数 $\{2^{4},2^{7}\}$ 为例计算步骤是: $2^{7}/2^{4}=2^{3},2^{4}/2^{3}=2^{1}$ , $2^{3}/2^{1}=2^{2},2^{2}/2^{1}=2,2^{1}/2^{1}=1$ 结束得a=2。这是一个辗转相除的过程。
对A中所有元素都执行这个过程就得到了a。

代码

from math import *
# 得到除1外的最小公因数
def gcd_sub(a, b):
    if a<b: a,b = b, a # 交换保证a>b
    if b==1: return a
    return gcd_sub(b, a//b)
n = int(input())
x = list(set(map(int,input ().split()))) # set有去重的作用,万一输入有相同的数
x.sort ()
n = len(x)
a = []
b =[]
for i in range(1, n):
    d = gcd(x[i],x[0])  # 与第一个数求比值
    a.append(x[i]//d)   # A序列
    b.append(x[0]//d)   # B序列
n = len(a)
up = a[0]   # 分子
down = b[0] # 分母
# 求分子分母的最小公因数
for i in range(1,n):
    up = gcd_sub(up, a[i])
    down = gcd_sub(down,b[i])
print('%d/%d'%(up, down))

例题五寻找整数

2022年第十三届省赛填空题lanaiao0J题号2131

问题描述

本题为填空题只需要算出结果后在代码中使用输出语句将所填结果输出即可。

有一个不超过 $10^{17}$ 的正整数 n知道这个数除以 2 至 49 后的余数如下表所示求这个正整数最小是多少。

解法一模拟

暴力法:一个个检验1～ $10^{17}$ 的每个数
由于这个数n最大可能是 $10^{17}$ 验证的时间太长。

如何减少验证时间?

如果n是某个数k的倍数那么可以递增k来验证for i in range(1, $10^{17}$ ,k)循环 $10^{17}$ /k次k越大验证的次数越少。
从表中看出n是11和17.的倍数,最小的k =11×17=187。
但是k仍然太小, $10^{17}$ /187≈ $10^{14}$ for循环 $10^{14}$ 次仍然耗时太长。即使用C++编码运行也需要 $10^6$ 秒)

如何找到一个较大的k?

证明满足表格中部分例如a= 4546474849)的n从小到大的n1、n2、n3、...它们是一个等差数列即n2-n1,= n3-n2= ...=k'。

cnt = 0
tmp=0
for i in range(187,10**17,187):
    if i % 49 ==46 and i % 48== 41 and i % 47 == 5 \
                   and i % 46 == 15 and i % 45 == 29:
        cnt += 1
        print(i,'k=', i-tmp)    # i-tmp是两次满足这五个要求的公差
        tmp=i
    if cnt > 3: break
# 5458460249 k= 5458460249
# 12590206409 k= 7131746160
# 19721952569 k= 7131746160
# 26853698729 k= 7131746160

先用Python编码求k'得k'=7131746160故从5458460249开始步长k=7131746160的等差数列

完全满足表格的从小到大的n1、n2、n3、...也是等差数列
n2-n1 = n3-n2= ... =k。k是k’的倍数。因为满足后五个要求是满足全部要求的子条件
用k’=7131746160作为for循环的步长暴力检验找到最小的n。
循环次数:1017/k’~14,000,000。

代码演示1

mod = [0,0,1,2,1,4,5,4,1,2,9,0,5,10,11,14,9,0,11,18,9,11,11,15 ,17,9,23,20,25,16,29,27,25,11,17,4,29,22,37,23,9,1,11,11,33,29,15,5,41,46]
for i in range (5458460249,10**17,7131746160):     #开始是5458460249,步长k=7131746160
    for a in range(2,50):
        if i % a != mod[a]:
            break
    else:               # for else结构: 若for正常结束,运行else语句
        print(i)        # 输出答案:2022040920220409
        break

解法二LCM

从表格的第一个数2开始逐个增加后面的数找满足条件的n。
1满足第一个条件除以2余1的数有:3、5、7、9、...此时步长k= 2。

2继续满足第二个条件除以3余2的数只能从上一步骤的3、5、7、9、...中找有5、11、17、...
此时步长k =6为什么k=6?

实际上是LCM: k = lcm(2,3)=6

证明:
设n1和n2满足:
n1= 2a1+1= 3b1+2
n2= 2a2+1 = 3b2+2
n2和n1的差k = n2-n1= 2(a2-a1)= 3(b2-b1)
k是2的倍数也是3的倍数那么k是2和3的最小公倍数k= lcm(2,3)=6。

3继续满足第三个条件除以4余1的数只能从5、11、17、...中找有5、17、29、...此时步长k = lcm(2,3,4)= 12。

4继续满足第四个条件....

逐个检查表格直到满足表格中所有的条件。

代码演示2

代码计算量极小只需要对表格中的2~49做48次LCM即可。

from math import *

mod = [0, 0, 1, 2, 1, 4, 5, 4, 1, 2, 9, 0, 5, 10, 11, 14, 9, 0, 11, 18, 9, 11, 11, 15, 17, 9, 23, 20, 25, 16, 29, 27,
       25, 11, 17, 4, 29, 22, 37, 23, 9, 1, 11, 11, 33, 29, 15, 5, 41, 46]
ans = 2 + mod[2]
k = 2  # 从第一个数的步长2开始
for i in range(3, 50):
    while 1:
        if ans % i == mod[i]:   # ans是满足前i个数的解
            k = lcm(k, int(i))  # 对当前步长k和i做LCM得到新的步长
            break
        else:
            ans += k            # ans不满足就累加当前步长k,直到ans满足前i个数的解
print(ans)

阿里云国内75折回扣微信号：monov8

阿里云国际，腾讯云国际，低至75折。AWS 93折免费开户实名账号代冲值优惠多多微信号：monov8 飞机：@monov6

返回列表

上一篇：webpack搭建的React脚手架项目与vite进行兼容化开发

下一篇：scala映射和元组