吴恩达《机器学习》——Logistics回归代码实现
| 阿里云国内75折 回扣 微信号:monov8 |
| 阿里云国际,腾讯云国际,低至75折。AWS 93折 免费开户实名账号 代冲值 优惠多多 微信号:monov8 飞机:@monov6 |
Logisitc回归
数据集、源文件可以在Github项目中获得
链接: https://github.com/Raymond-Yang-2001/AndrewNg-Machine-Learing-Homework
1. Sigmoid与二分类
与线性回归不同Logistic回归虽然名为回归却常常被用来实现分类的功能。其与线性回归的不同之处仅仅在于在线性回归的输出后添加了一个Sigmoid函数使其输出能表示分类的概率而不会预测值。至于为什么Sigmoid函数会有这样的功能我们在接下来会说明。
Sigmoid函数
Sigmoid函数的数学表达式如下所示
σ
(
x
)
=
1
1
+
e
−
x
\sigma(x)=\frac{1}{1+e^{-x}}
σ(x)=1+e−x1
分析可得Sigmoid函数是一个递增函数x值越大
σ
(
x
)
\sigma(x)
σ(x)越接近1x值越小
σ
(
x
)
\sigma(x)
σ(x)越接近0。当x=0的时候
σ
(
x
)
=
0.5
\sigma(x)=0.5
σ(x)=0.5。其函数曲线图如下所示
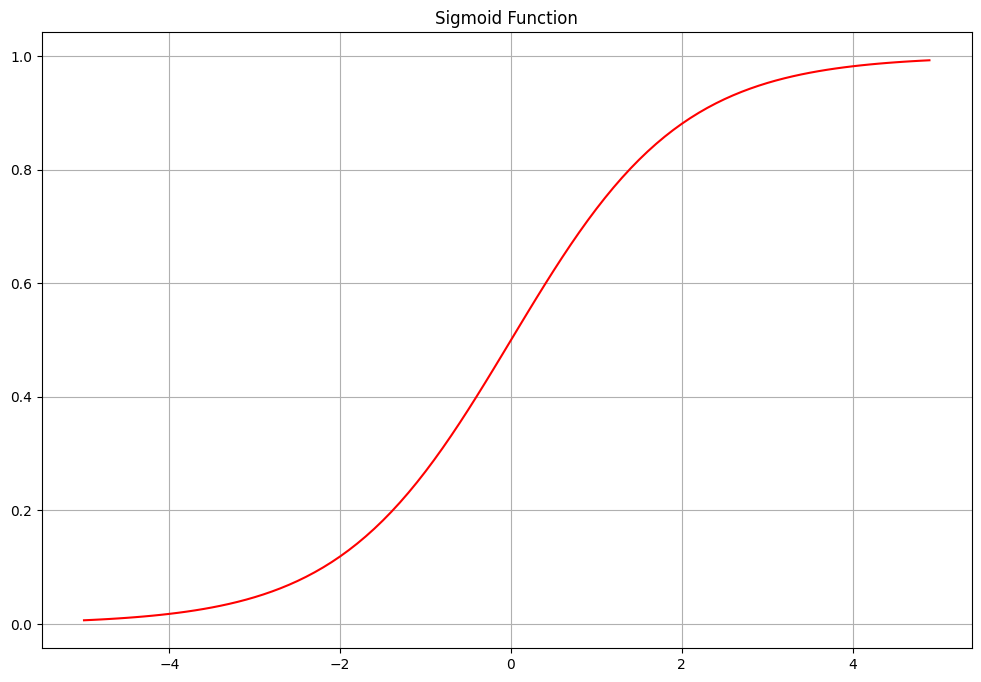
为什么Sigmoid函数可以表示二分类概率
这里我们先来回顾一下伯努利分布的知识。
伯努利分布指的是对于随机变量 X X X有, 参数为 p ( 0 < p < 1 ) p(0<p<1) p(0<p<1)如果它分别以概率 p p p和 1 − p 1-p 1−p取1和0为值。 E ( X ) = p E(X)= p E(X)=p, D ( X ) = p ( 1 − p ) D(X)=p(1-p) D(X)=p(1−p)。伯努利试验成功的次数服从伯努利分布,参数 p p p是试验成功的概率。伯努利分布是一个离散型机率分布是 N = 1 N=1 N=1时二项分布的特殊情况
对于伯努利分布我们有
p
=
μ
x
(
1
−
μ
)
(
1
−
x
)
p=\mu^{x}(1-\mu)^{(1-x)}
p=μx(1−μ)(1−x)对等式做变换有
p
=
e
x
ln
μ
+
(
1
−
x
)
ln
(
1
−
μ
)
=
e
x
ln
μ
1
−
μ
+
ln
(
1
−
μ
)
p=e^{x\ln{\mu}+(1-x)\ln{(1-\mu)}}=e^{x\ln{\frac{\mu}{1-\mu}}+\ln{(1-\mu)}}
p=exlnμ+(1−x)ln(1−μ)=exln1−μμ+ln(1−μ)
接下来我们使用指数族分布来表示伯努利分布。
指数族分布(exponential family of distributions)亦称指数型分布族是统计中最重要的参数分布族
指数族分布的一般参数化表示为
p
(
y
;
η
)
=
b
(
y
)
e
η
⊤
T
(
y
)
−
α
(
η
)
p(y;\eta)=b(y)e^{\eta^{\top}T(y)-\alpha(\eta)}
p(y;η)=b(y)eη⊤T(y)−α(η)
其中
- y y y是自然参数
- T ( y ) T(y) T(y)是 y y y的充分统计量
- α ( η ) \alpha(\eta) α(η)是对数部分函数用来确保 ∑ p ( y ; η ) = 1 \sum{p(y;\eta)}=1 ∑p(y;η)=1
由此式可以得到
η
=
ln
μ
1
−
μ
\eta=\ln{\frac{\mu}{1-\mu}}
η=ln1−μμ即
μ
=
1
1
+
e
−
η
\mu=\frac{1}{1+e^{-\eta}}
μ=1+e−η1
由此可得Sigmoid函数是可以表示伯努利分布的概率的。
2. Logistics回归
与线性回归一样Logistic回归同样可以采用基于梯度的优化方法来求解。Logistic回归的模型公式如下所示
h
(
x
;
θ
)
=
σ
(
θ
x
⊤
)
h(\boldsymbol{x};\boldsymbol{\theta})=\sigma{(\boldsymbol{\theta x^{\top}})}
h(x;θ)=σ(θx⊤)
其中
x
\boldsymbol{x}
x是维度为
(
n
,
d
+
1
)
(n,d+1)
(n,d+1)的样本补充添加第一维度全为1便于偏置项的运算
θ
\boldsymbol{\theta}
θ为
(
1
,
d
+
1
)
(1,d+1)
(1,d+1)的参数。得到
(
1
,
n
)
(1,n)
(1,n)的输出。
交叉熵损失函数
在线性回归中我们可以使用均方误差MSE来衡量预测值和真实值之间的差异这种基于数值差异的损失函数很容易被理解。但是在分类任务当中MSE显然已经不适合衡量分类的差异了为此我们引入了一个全新的损失函数——交叉熵损失。
为了理解交叉熵损失我们先从信息论的一个重要概念——KL散度入手。
在分类任务当中无论是多分类还是二分类我们的任务可以看做要输出一个预测的分布。对于二分类这是一个伯努利分布对于多分类这是一个多项式分布。分类的效果越好这个输出的分布和目标分布应当越接近。那么如何衡量两个分布的相似度这就是KL散度的作用。
考虑一个
K
K
K类的分类问题设我们的目标分布为
q
(
k
∣
x
)
q(k|x)
q(k∣x)输出的分布为
p
(
k
∣
x
)
p(k|x)
p(k∣x)。这两个分布分别指明了样本为第
k
k
k类的概率。对于目标分布显而易见这是一个one-hot样式的分布即在真是类别的概率为1其余概率均为0。两个分布的KL散度写作
K
L
(
q
∣
∣
p
)
=
∑
k
=
1
K
q
(
k
∣
x
)
log
q
(
k
∣
x
)
p
(
k
∣
x
)
KL(q||p)=\sum_{k=1}^{K}{q(k|x)\log{\frac{q(k|x)}{p(k|x)}}}
KL(q∣∣p)=k=1∑Kq(k∣x)logp(k∣x)q(k∣x)
两个分布越接近KL散度越小。可以观察到当
p
=
q
p=q
p=q的时候KL散度为0。
如果我们将KL散度进一步展开可以得到
K
L
(
q
∣
∣
p
)
=
∑
k
=
1
K
q
(
k
∣
x
)
log
q
(
k
∣
x
)
−
q
(
k
∣
x
)
log
p
(
k
∣
x
)
KL(q||p)=\sum_{k=1}^{K}{q(k|x)\log{q(k|x)}-q(k|x)\log{p(k|x)}}
KL(q∣∣p)=k=1∑Kq(k∣x)logq(k∣x)−q(k∣x)logp(k∣x)
前半部分是关于分布
q
q
q的常数考虑到分布
q
q
q是固定的目标分布KL散度只与后半部分有关也被叫做交叉熵。
C
r
o
s
s
E
n
t
r
o
p
y
=
−
∑
k
=
1
K
q
(
k
∣
x
)
log
p
(
k
∣
x
)
CrossEntropy=-\sum_{k=1}^{K}q(k|x)\log{p(k|x)}
CrossEntropy=−k=1∑Kq(k∣x)logp(k∣x)
两个分布越接近交叉熵越小反之交叉熵越大。
特别地对于二分类任务存在二分类交叉熵BCE(Binary Cross Entropy)
B
C
E
=
−
(
y
log
y
^
+
(
1
−
y
)
log
(
1
−
y
^
)
)
BCE=-(y\log{\hat{y}}+(1-y)\log{(1-\hat{y})})
BCE=−(ylogy^+(1−y)log(1−y^))
这其实是
K
=
2
K=2
K=2的特殊情况。
梯度
Logistic回归的梯度表示与线性回归一样都为
θ
j
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
(
x
(
i
)
;
θ
)
−
y
(
i
)
)
x
j
(
i
)
\theta_{j}=\theta_{j}-\alpha\frac{1}{m}\sum_{i=1}^{m}{(h(x^{(i)};\theta)-y^{(i)})x_{j}^{(i)}}
θj=θj−αm1i=1∑m(h(x(i);θ)−y(i))xj(i)
注意在Logistic回归中
h
(
x
;
θ
)
=
σ
(
θ
x
⊤
)
h(\boldsymbol{x};\boldsymbol{\theta})=\sigma{(\boldsymbol{\theta x^{\top}})}
h(x;θ)=σ(θx⊤)在线性回归中则没有Sigmoid的运算。
具体推导如下
J
(
θ
)
=
−
[
y
log
p
+
(
1
−
y
)
log
(
1
−
p
)
]
J(\boldsymbol{\theta})=-\left[ y\log{p}+(1-y)\log{(1-p)}\right]
J(θ)=−[ylogp+(1−y)log(1−p)]
其中
p
=
σ
(
θ
x
)
p=\sigma(\boldsymbol{\theta x})
p=σ(θx)。
由线性法则
∂
J
∂
θ
j
=
∂
J
∂
p
∂
p
∂
(
θ
x
)
∂
(
θ
x
)
∂
θ
j
\frac{\partial{J}}{\partial{\theta_{j}}}=\frac{\partial{J}}{\partial{p}}\frac{\partial{p}}{\partial{(\boldsymbol{\theta x})}}\frac{\partial{(\boldsymbol{\theta x})}}{\partial{\theta_{j}}}
∂θj∂J=∂p∂J∂(θx)∂p∂θj∂(θx)
其中
- ∂ J ∂ p = − y p + 1 − y 1 − p \frac{\partial{J}}{\partial{p}}=-\frac{y}{p}+\frac{1-y}{1-p} ∂p∂J=−py+1−p1−y
- ∂ p ∂ ( θ x ) = σ ( θ x ) ( 1 − σ ( θ x ) ) \frac{\partial{p}}{\partial{(\boldsymbol{\theta x})}}=\sigma(\boldsymbol{\theta x})(1-\sigma{(\boldsymbol{\theta x})}) ∂(θx)∂p=σ(θx)(1−σ(θx))
- ∂ ( θ x ) ∂ θ j = x j \frac{\partial{(\boldsymbol{\theta x})}}{\partial{\theta_{j}}}=x_{j} ∂θj∂(θx)=xj
三个式子相乘有
J
(
θ
)
=
[
−
y
p
+
1
−
y
1
−
p
]
σ
(
θ
x
)
(
1
−
σ
(
θ
x
)
)
x
j
=
[
−
y
σ
(
θ
x
)
+
1
−
y
1
−
σ
(
θ
x
)
]
σ
(
θ
x
)
(
1
−
σ
(
θ
x
)
)
x
j
=
[
−
y
(
1
−
σ
(
θ
x
)
)
+
(
1
−
y
)
σ
(
θ
x
)
]
x
j
=
(
σ
(
θ
x
)
−
y
)
x
j
\begin{aligned} J(\boldsymbol{\theta})&=\left[-\frac{y}{p}+\frac{1-y}{1-p}\right]\sigma(\boldsymbol{\theta x})(1-\sigma{(\boldsymbol{\theta x})})x_{j} \\ &=\left[-\frac{y}{\sigma(\boldsymbol{\theta x})}+\frac{1-y}{1-\sigma(\boldsymbol{\theta x})}\right]\sigma(\boldsymbol{\theta x})(1-\sigma{(\boldsymbol{\theta x})})x_{j}\\ &=\left[-y(1-\sigma(\boldsymbol{\theta x}))+(1-y)\sigma(\boldsymbol{\theta x})\right]x_{j}\\ &=(\sigma(\boldsymbol{\theta x})-y)x_{j} \end{aligned}
J(θ)=[−py+1−p1−y]σ(θx)(1−σ(θx))xj=[−σ(θx)y+1−σ(θx)1−y]σ(θx)(1−σ(θx))xj=[−y(1−σ(θx))+(1−y)σ(θx)]xj=(σ(θx)−y)xj
过拟合与欠拟合
在机器学习领域过拟合始终是一个重要的问题。过拟合指的是学习到的模型偏差小方差过大的情况。
举例来说存在一个较大的分类用数据集这个数据集的标签符合一定的分布模型的目标是学习从样本到这个分布的映射。假设我们将这个数据集随机分成10个子集分别训练出对应的十个模型这十个模型应当都能在自己的数据集上进行较好地分类同时模型的之间的差距应该不会很大——因为所有的数据都来自一个数据集。这就意味着模型的偏差和方差都比较小。
考虑一种情况假设其中一个数据集中包括的“狗”的样本都是白色的狗这个模型认为所有白色的动物就都是狗。这虽然能在“白狗”的数据集上进行很好地分类但是相较于其他模型这个模型的“差异”显得过大。这就是偏差小的情况下方差变大。也叫做过拟合。
反之如果偏差很大方差很小即模型之间的差异都很小但都不能准确分类这种情况叫做欠拟合。
对于欠拟合我们可以通过数据增强或者暴力提高迭代次数来解决。对于过拟合我们将介绍一种叫做正则化的方法。
正则化
最常用的正则化方式是在损失函数后面附加一个参数的惩罚项以控制参数不要向过拟合的方向发展。通用的表达形式为
R
e
g
u
l
a
r
i
z
e
d
l
o
s
s
=
L
o
s
s
+
λ
(
θ
)
Regularized\ loss = Loss + \lambda(\theta)
Regularized loss=Loss+λ(θ)
在本代码中我们实现
L
2
L^{2}
L2正则化。
正则化损失函数如下所示
J
(
θ
)
=
1
m
∑
i
=
1
m
[
−
y
(
i
)
log
(
h
θ
(
x
(
i
)
)
)
−
(
1
−
y
(
i
)
)
log
(
1
−
h
θ
(
x
(
i
)
)
)
]
+
λ
2
m
∑
j
=
1
n
θ
j
2
J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}}
J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
我们对其求梯度可以得到正则化后的梯度
g
(
θ
)
=
1
m
∑
i
=
1
m
(
h
(
x
(
i
)
;
θ
)
−
y
(
i
)
)
x
j
(
i
)
+
λ
m
θ
j
g(\theta)=\frac{1}{m}\sum_{i=1}^{m}{(h(x^{(i)};\theta)-y^{(i)})x_{j}^{(i)}}+\frac{\lambda }{m}\theta _{j}
g(θ)=m1i=1∑m(h(x(i);θ)−y(i))xj(i)+mλθj
利用正则化的梯度更新参数可以得到
θ
j
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
(
x
(
i
)
;
θ
)
−
y
(
i
)
)
x
j
(
i
)
−
λ
m
∑
j
=
1
n
θ
j
=
(
1
−
λ
m
)
θ
j
−
α
1
m
∑
i
=
1
m
(
h
(
x
(
i
)
;
θ
)
−
y
(
i
)
)
x
j
(
i
)
\theta_{j}=\theta_{j}-\alpha\frac{1}{m}\sum_{i=1}^{m}{(h(x^{(i)};\theta)-y^{(i)})x_{j}^{(i)}}-\frac{\lambda }{m}\sum\limits_{j=1}^{n}{\theta _{j}}=\left(1-\frac{\lambda }{m}\right)\theta_{j}-\alpha\frac{1}{m}\sum_{i=1}^{m}{(h(x^{(i)};\theta)-y^{(i)})x_{j}^{(i)}}
θj=θj−αm1i=1∑m(h(x(i);θ)−y(i))xj(i)−mλj=1∑nθj=(1−mλ)θj−αm1i=1∑m(h(x(i);θ)−y(i))xj(i)
可以看出正则化实际上是对参数进行了一定程度的缩小。缩小的程度与
λ
/
m
\lambda / m
λ/m 有关。
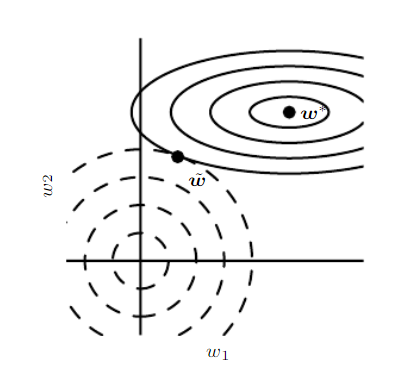
此图说明了
L
2
L^{2}
L2正则化的参数的影响。虚线表示正则化项的损失等值线实线表示未正则化损失函数的损失等值线。两者在
w
~
\tilde{w}
w~达到平衡。在
w
1
w_{1}
w1方向参数变化的时候损失函数并不会变化太多但在
w
2
w_{2}
w2这种变化显得更为剧烈。也就是说
w
2
w_{2}
w2相比
w
1
w_{1}
w1更能显著地减小损失函数值。
L 2 L^{2} L2正则化使得显著减小损失函数值方向上的参数保存更完好无助于损失函数减小的方向改变较大因为这不会显著的影响梯度。
3. Python代码实现
这里给出Logistic回归类的代码 同时也实现了数据的归一化和正则化
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def bce_loss(pred, target):
"""
计算误差
:param pred: 预测
:param target: ground truth
:return: 损失序列
"""
return -np.mean(target * np.log(pred) + (1-target) * np.log(1-pred))
class LogisticRegression:
"""
Logistic回归类
"""
def __init__(self, x, y, val_x, val_y, epoch=100, lr=0.1, normalize=True, regularize=None, scale=0, show=True):
"""
初始化
:param x: 样本, (sample_number, dimension)
:param y: 标签, (sample_numer, 1)
:param epoch: 训练迭代次数
:param lr: 学习率
"""
self.theta = None
self.loss = []
self.val_loss = []
self.n = x.shape[0]
self.d = x.shape[1]
self.epoch = epoch
self.lr = lr
t = np.ones(shape=(self.n, 1))
self.normalize = normalize
if self.normalize:
self.x_std = x.std(axis=0)
self.x_mean = x.mean(axis=0)
self.y_mean = y.mean(axis=0)
self.y_std = y.std(axis=0)
x = (x - self.x_mean) / self.x_std
self.y = y
self.x = np.concatenate((t, x), axis=1)
# self.val_x = (val_x - val_x.mean(axis=0)) / val_x.std(axis=0)
self.val_x = val_x
self.val_y = val_y
self.regularize = regularize
self.scale = scale
self.show = show
def init_theta(self):
"""
初始化参数
:return: theta (1, d+1)
"""
self.theta = np.zeros(shape=(1, self.d + 1))
def gradient_decent(self, pred):
"""
实现梯度下降求解
"""
# error (n,1)
error = pred - self.y
# term (d+1, 1)
term = np.matmul(self.x.T, error)
# term (1,d+1)
term = term.T
if self.regularize == "L2":
re = self.scale / self.n * self.theta[0, 1:]
re = np.expand_dims(np.array(re), axis=0)
re = np.concatenate((np.array([[0]]), re), axis=1)
# re [0,...] (1,d+1)
self.theta = self.theta - self.lr * (term / self.n + re)
# update parameters
else:
self.theta = self.theta - self.lr * (term / self.n)
def validation(self, x, y):
if self.normalize:
x = (x - x.mean(axis=0)) / x.std(axis=0)
outputs = self.get_prob(x)
curr_loss = bce_loss(outputs, y)
if self.regularize == "L2":
curr_loss += self.scale / self.n * np.sum(self.theta[0, 1:] ** 2)
self.val_loss.append(curr_loss)
predicted = np.expand_dims(np.where(outputs[:, 0] > 0.5, 1, 0), axis=1)
count = np.sum(predicted == y)
if self.show:
print("Accuracy on Val set: {:.2f}%\tLoss on Val set: {:.4f}".format(count / y.shape[0] * 100, curr_loss))
def test(self, x, y):
outputs = self.get_prob(x)
predicted = np.expand_dims(np.where(outputs[:, 0] > 0.5, 1, 0), axis=1)
count = np.sum(predicted == y)
# print("Accuracy on Test set: {:.2f}%".format(count / y.shape[0] * 100))
# curr_loss = bce_loss(outputs, y)
# if self.regularize == "L2":
# curr_loss += self.scale / self.n * np.sum(self.theta[0, 1:] ** 2)
return count / y.shape[0] # , curr_loss
def train(self):
"""
训练Logistic回归
:return: 参数矩阵theta (1,d+1); 损失序列 loss
"""
self.init_theta()
for i in range(self.epoch):
# pred (1,n); theta (1,d+1); self.x.T (d+1, n)
z = np.matmul(self.theta, self.x.T).T
# pred (n,1)
pred = sigmoid(z)
curr_loss = bce_loss(pred, self.y)
if self.regularize == "L2":
curr_loss += self.scale / self.n * np.sum(self.theta[0, 1:] ** 2)
self.loss.append(curr_loss)
self.gradient_decent(pred)
if self.show:
print("Epoch: {}/{}, Train Loss: {:.4f}".format(i + 1, self.epoch, curr_loss))
self.validation(self.val_x, self.val_y)
if self.normalize:
y_mean = np.mean(z, axis=0)
self.theta[0, 1:] = self.theta[0, 1:] / self.x_std.T
self.theta[0, 0] = y_mean - np.dot(self.theta[0, 1:], self.x_mean.T)
return self.theta, self.loss, self.val_loss
def get_prob(self, x):
"""
回归预测
:param x: 输入样本 (n,d)
:return: 预测结果 (n,1)
"""
t = np.ones(shape=(x.shape[0], 1))
x = np.concatenate((t, x), axis=1)
pred = sigmoid(np.matmul(self.theta, x.T))
return pred.T
def get_inner_product(self, x):
t = np.ones(shape=(x.shape[0], 1))
x = np.concatenate((t, x), axis=1)
return np.matmul(self.theta, x.T)
def predict(self, x):
prob = self.get_prob(x)
return np.expand_dims(np.where(prob[:, 0] > 0.5, 1, 0), axis=1)
4. 单维与多维Logistic分类
单维数据分类
数据集可视化
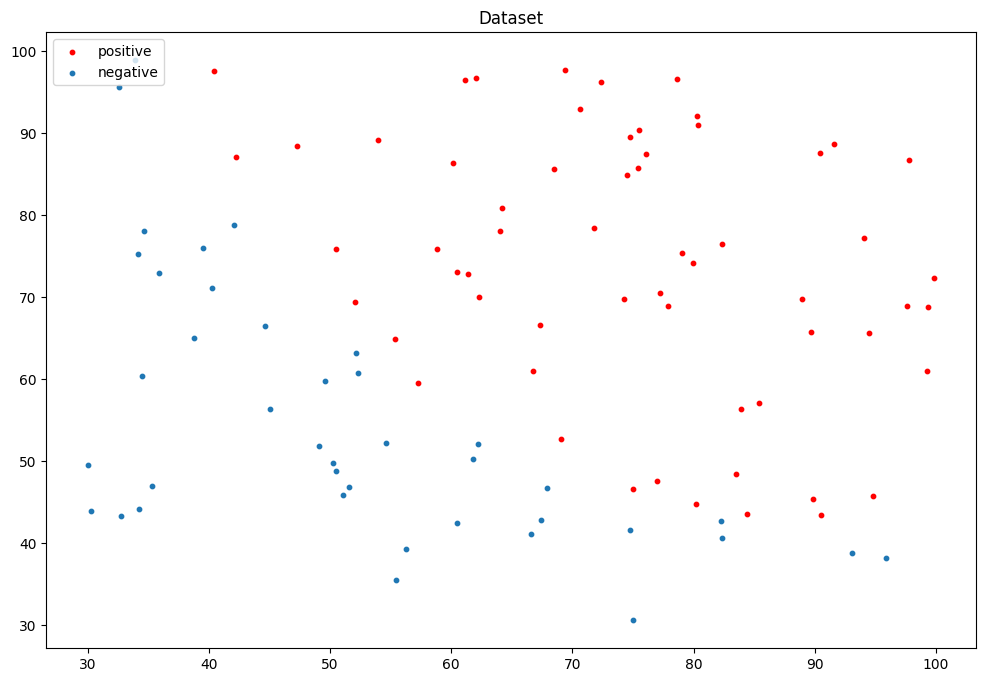
划分训练集和验证集
训练集可视化
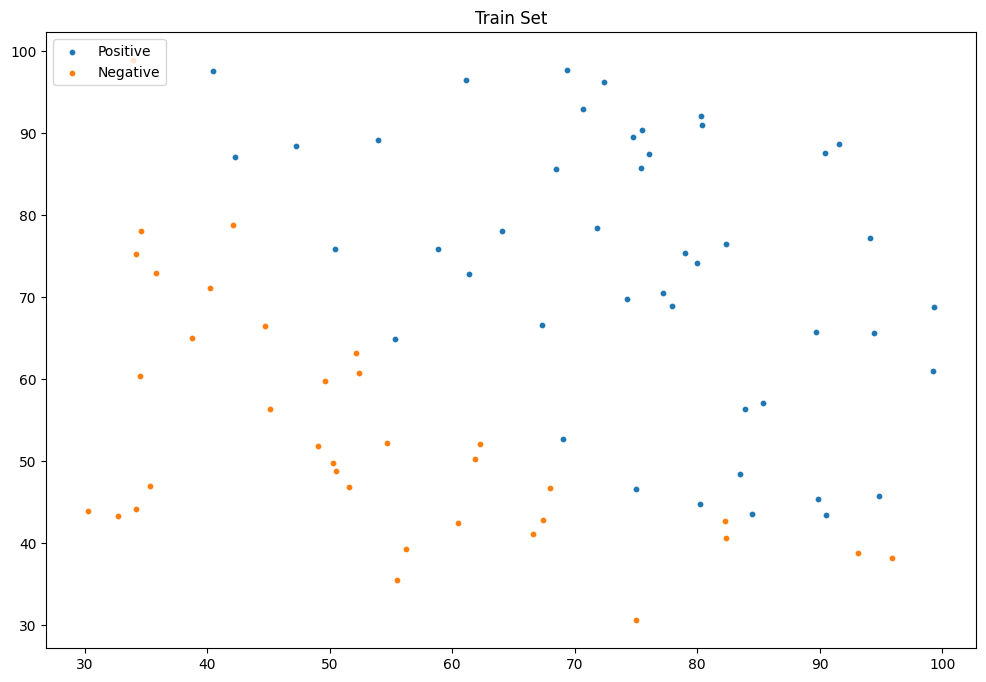
验证集可视化
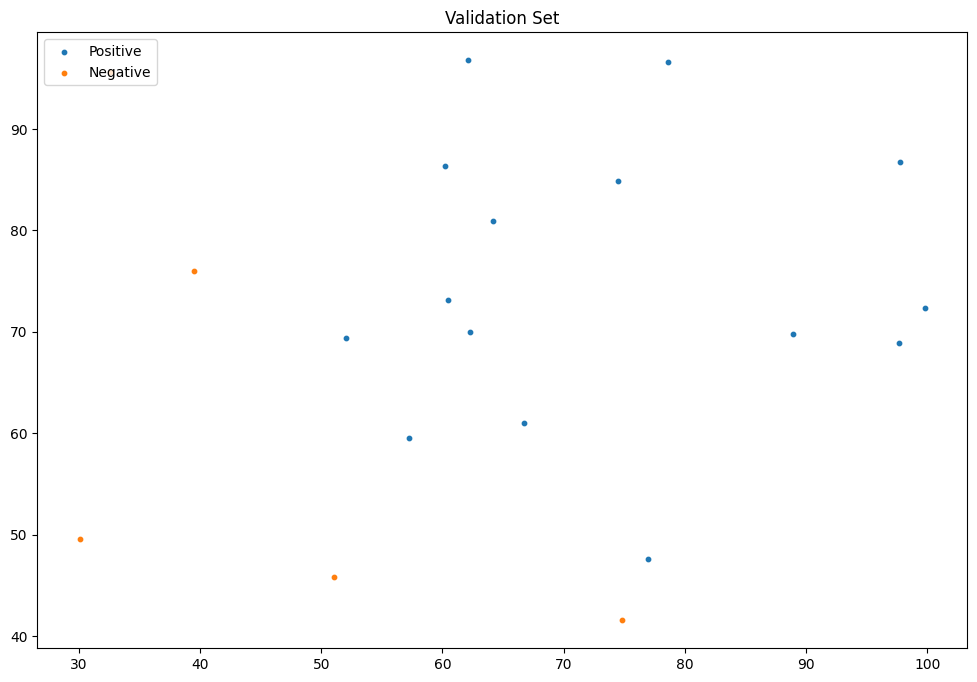
调用算法进行分类
from LogisticRegression import LogisticRegression
epochs = 5000
alpha = 0.01
logistic_reg = LogisticRegression(x=train_x,y=train_y_ex,val_x=val_x,val_y=val_y_ex,epoch=epochs,lr=alpha)
theta,train_loss,val_loss = logistic_reg.train()
分类性能
Accuracy on Test Set: 80.00%
My F1 Score: 0.8571
sklearn库函数验证
Sklearn Accuracy: 80.00%
Sklearn F1 Score: 0.8571
决策边界可视化
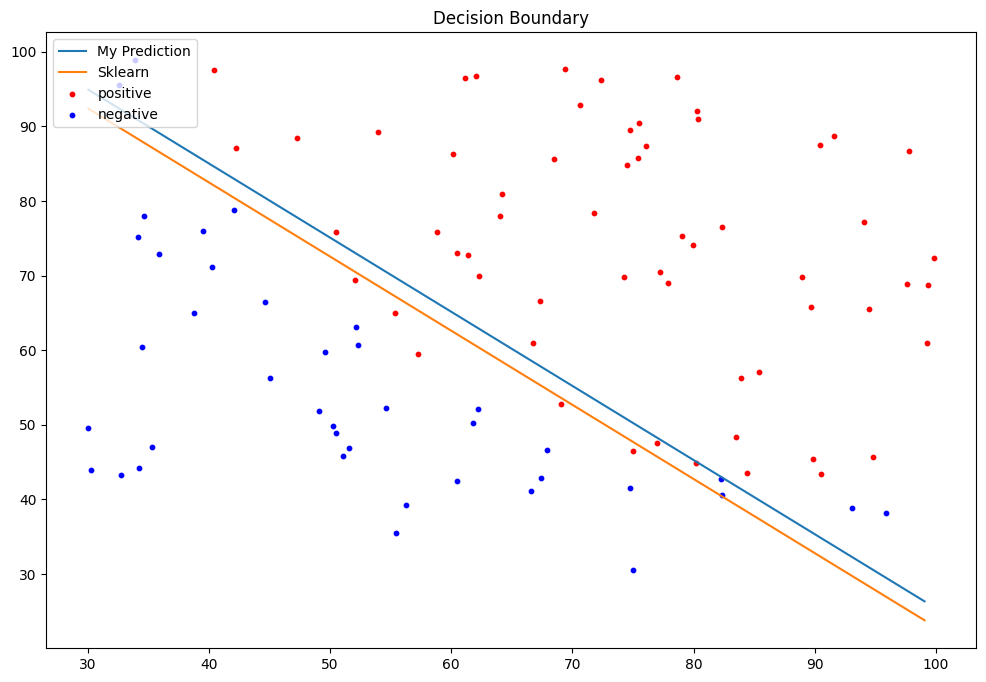
训练过程可视化
可以看到有明显的过拟合出现这可以通过调整学习率和迭代次数等来抑制过拟合当然也可以进行正则化。
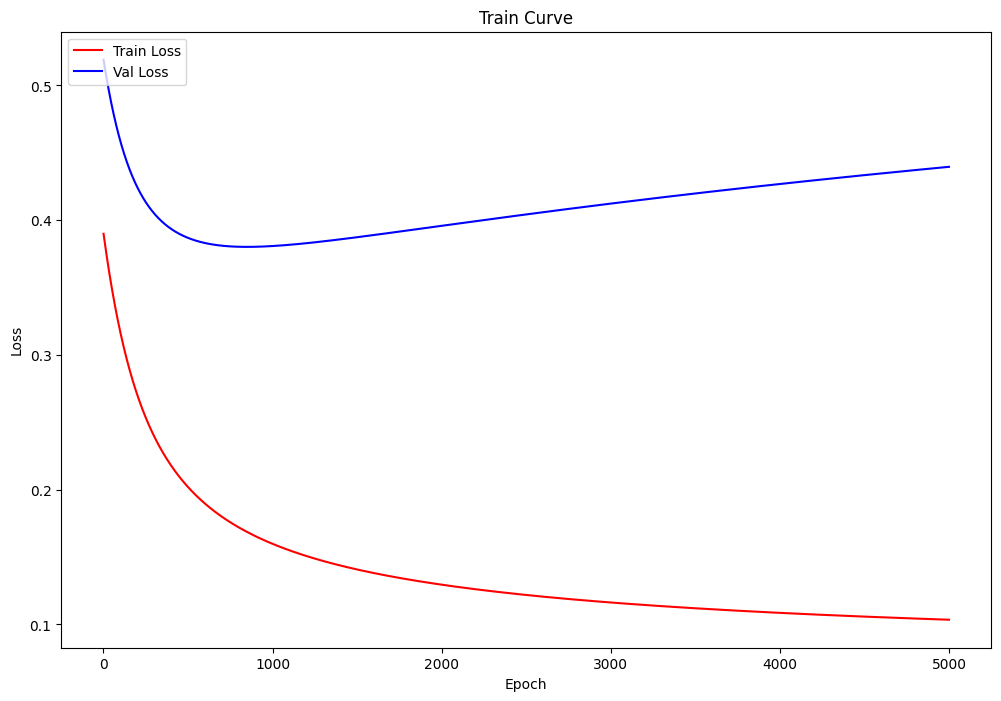
多维数据分类
数据集可视化
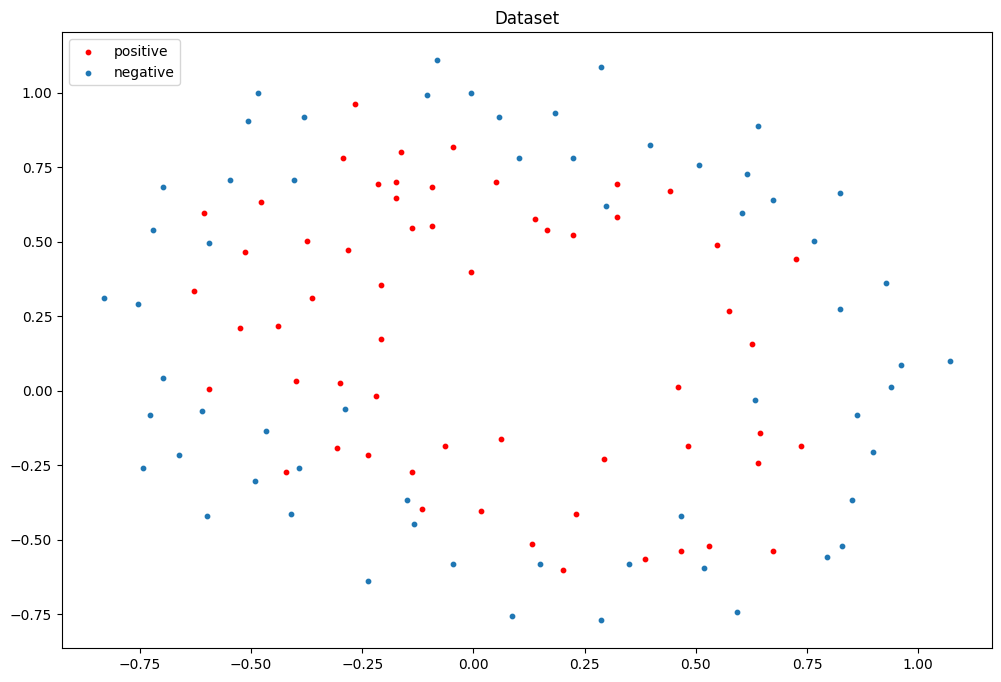
划分训练集和验证集
训练集
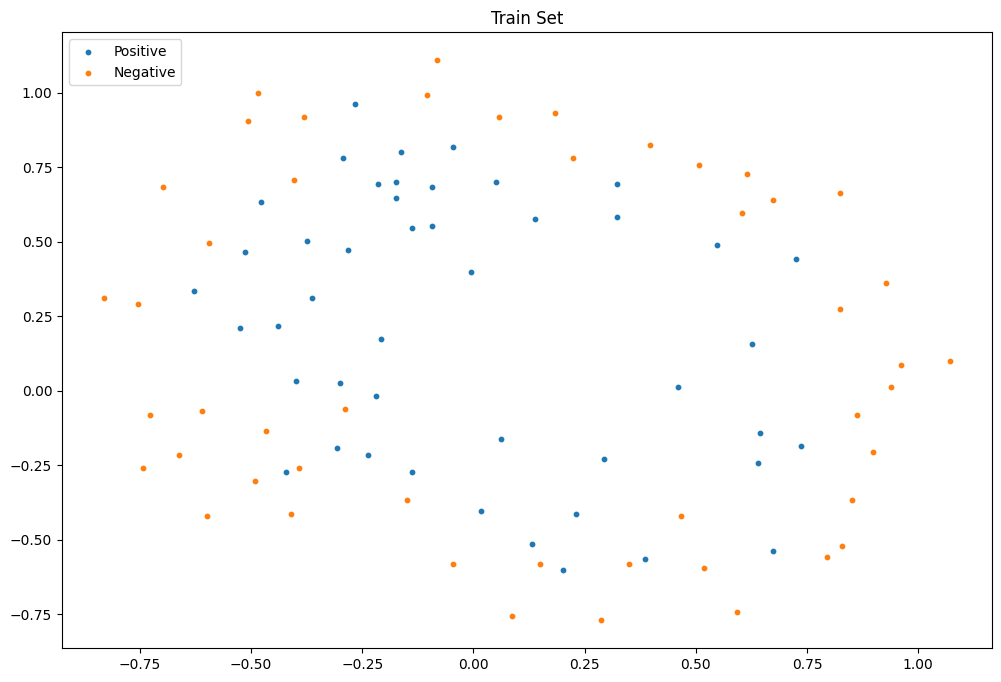
验证集
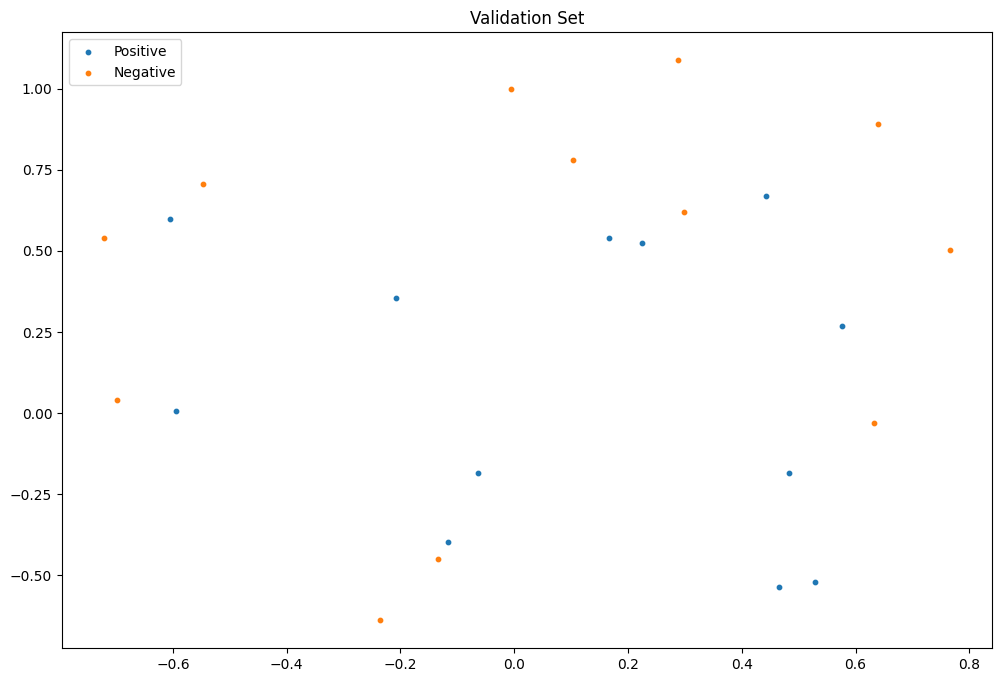
做数据增强拓展数据维度
X
=
[
x
1
,
x
2
,
x
1
2
,
x
1
x
2
,
x
2
2
,
x
1
3
,
x
1
2
x
2
,
⋯
]
\mathbf{X}=[x_{1}, x_{2}, x_{1}^{2}, x_{1}x_{2}, x_{2}^{2}, x_{1}^{3}, x_{1}^{2}x_{2},\cdots]
X=[x1,x2,x12,x1x2,x22,x13,x12x2,⋯]
这里扩展到六次方
def feature_mapping(x, degree):
feature = np.zeros([x.shape[0],1])
for i in range(0, 1 + degree):
for j in range(0, 1 + degree - i):
if i==0 and j==0: continue
feature=np.concatenate((feature, np.expand_dims(np.multiply(np.power(x[:, 0], i) , np.power(x[:, 1], j)), axis=1)),axis=1)
return feature[:,1:]
train_x_map = feature_mapping(train_x,degree=6)
val_x_map = feature_mapping(val_x,degree=6)
正则化参数为2
Accuracy on Test Set: 66.67%
My F1 Score: 0.5556
Sklearn Accuracy: 70.83%
Sklearn Val Loss: 0.3076
Sklearn F1 Score: 0.6667
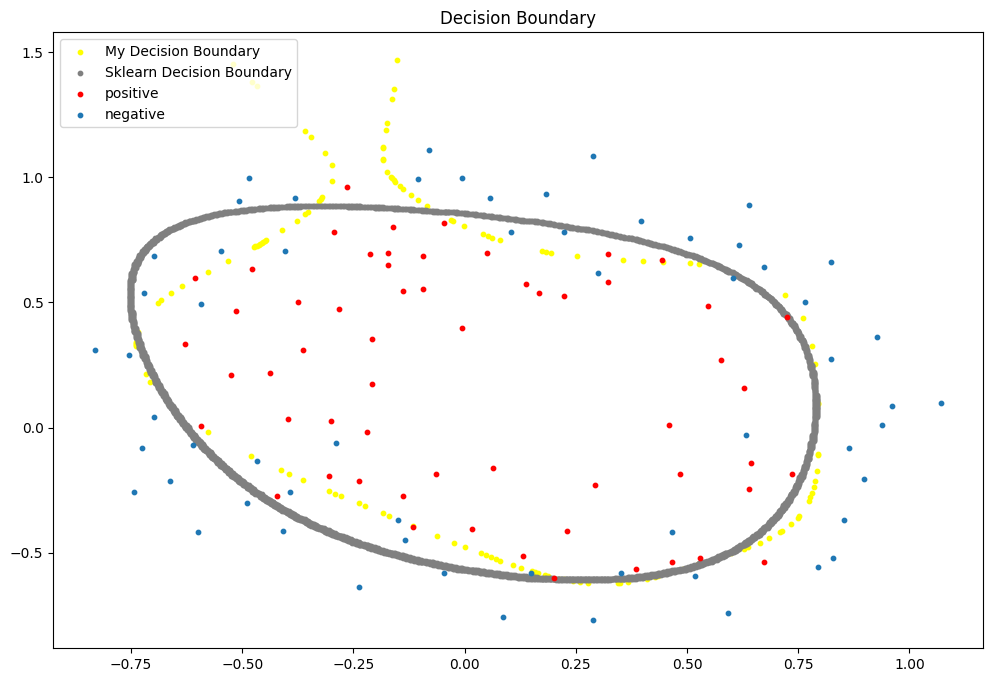
决策边界可视化
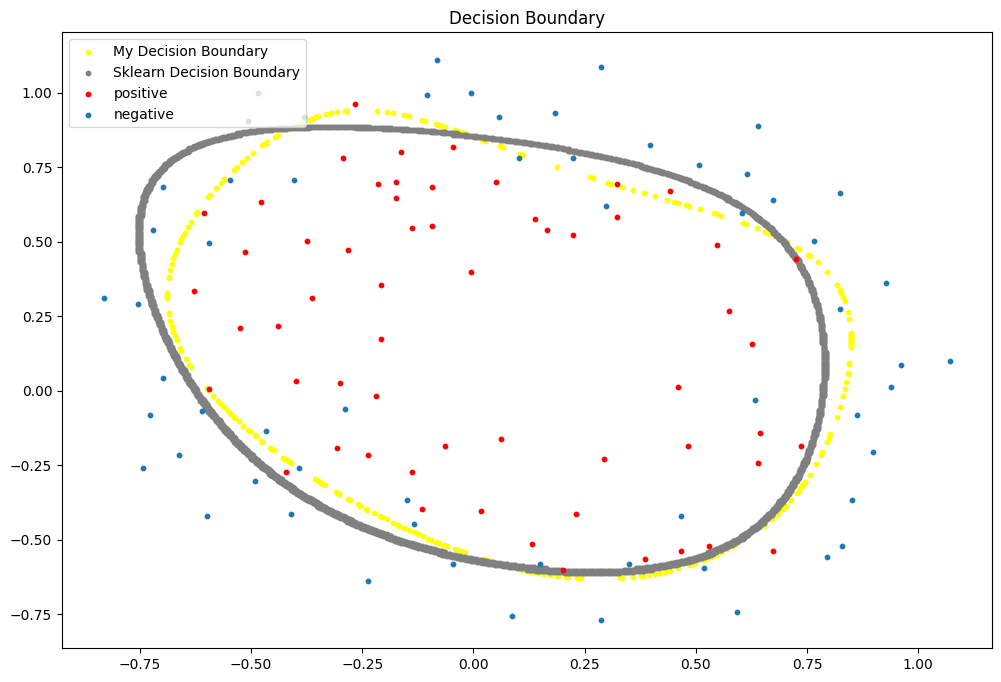
正则化参数为0决策边界可视化
可以看出决策边界显得过于“畸形”这是过拟合的突出表现。